和田玉超声波振动深孔钻削特性分析

廖结安，刘新英

(塔里木大学机械电气化工程学院，新疆阿拉尔843300)

中国有句俗话“玉不琢，不成器”，实践证明各种玉石只有经过巧妙构思和精雕细刻，才能最大限度地体现其昂贵的商业价值和艺术价值。钻孔是玉石雕刻工艺中重要一环，目前常用的钻孔方式有机械钻孔和超声波振动钻孔;其中针对和田玉超声波振动钻孔机制的研究较少，深孔钻方面就更少。和田玉由透闪石［1－2］Ca2(Mg，Fe2+)5［Si8O22］(OH)2微粒矿物集合体组成，主要为致密块状构造，质地细腻;主要结构为毛毡状变晶结构，其次为放射状变晶结构和纤维状柱状变晶结构。和田玉硬度经测定摩氏硬度为6.5 ～6.9，和田玉韧度极大(韧度也称为研磨硬度)，和田玉的研磨硬度可以达到摩氏硬度为9。但是，和田玉石的韧性与金属材料的物理学上所谓的韧性有很大不同，和田玉石的抗磨损、抗拉伸、抗压入的能力强，雕刻加工方面，和田玉一般钻孔方法很难入钻，钻孔也容易产生裂纹破损;超声波振动钻孔提高了玉石钻孔效率，破损率有较大的降低。

开展对和田玉超声波振动深孔钻削系统的研究，为探明和田玉材料的超声高效韧性深孔钻削机制，进一步推动其在生产实际中应用;并提出防裂纹破损的策略，对和田玉精密雕刻加工具有重要意义，同时也是研究其他高硬度、高韧性材料的深孔加工机制的有益探索。

1 超声波轴向振动深孔钻削的运动形式

超声波振动钻削技术［3－8］是建立在金属切削理论和振动理论基础上的一种新的钻削加工方法，属于振动钻削的一个分支;超声波振动钻削加工过程中，通过超声振动装置使钻头与工件之间产生可控的相对振动;钻削过程就变为瞬时的、脉冲的动态钻削过程，与普通钻削的机制发生了很大的变化。钻削运动过程可以简化为图1所示的模型。

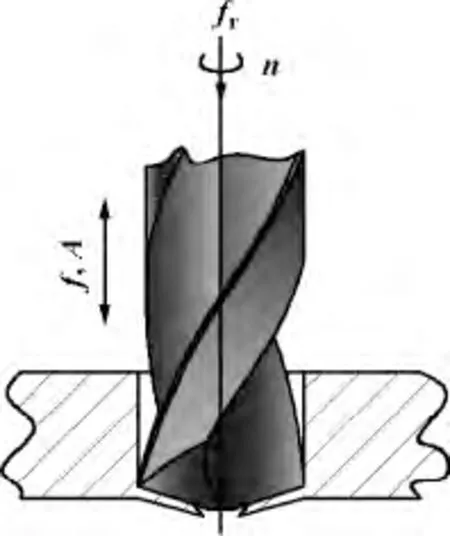
图1 超声振动深孔钻削模型

2 和田玉超声波振动深孔钻削切削厚度变化特性

图1 是和田玉超声波轴向振动深孔钻削的基本模型。附加给深孔钻头上的轴向振动位移为:ZP=Asin(2πft)。则深孔钻削加工过程中钻头刀刃上任一点实际轴向进给量Z 可表示为:

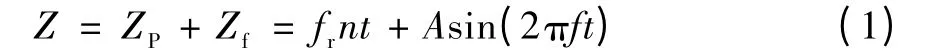
式中:Z 为钻尖的实际轴进给量，mm;ZP为钻头轴向振动位移，mm;Zf为钻头轴向进给位移，mm;fr为钻头的每转进给量，mm/r;n 为工件转速，r/s;t为切削时间，s;f 为轴向振动频率，Hz;A 为轴向振幅，mm。

和田玉超声波振动深孔钻削过程中，钻尖的扭转角位移为:θ =2πnt，代入式(2)中可得到和田玉超声波轴向振动深孔钻削实际切削厚度为:

式中:θ 为钻头的扭转角位移，rad。

如图2所示，选择钻头进给量为0.08 mm/r，轴向振幅为0.05 mm，钻头在一个圆周内实际进给量变化如图中浅色曲线所示。图中纵坐标为钻头进给量，横坐标为钻头角位移。通过对钻头在一个圆周内实际进给量变化的分析，钻头切削厚度是根据振动系统变化而变化，是一个动态的过程。这就是和田玉超声波轴向振动钻削的变厚切削特性。

如图3所示，选择钻头进给量为0.02 mm/r，轴向振幅为0.05 mm，钻头在一个圆周内实际进给量变化如图中浅色曲线所示。图中纵坐标为钻头进给量，横坐标为钻头角位移。分析图3 可以看出，钻头在一个圆周内的钻削过程中出现空钻现象，出现空钻现象与钻削进给量参数与振动的振幅有关系，钻削进给量小于振动的振幅就会出现空钻现象。在和田玉超声波轴向振动深孔钻削过程中，动态轴向钻削厚度是周期变化的;当Z ＞0 时表示实切材料，Z≤0 时为空切。

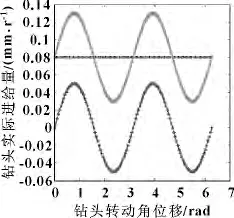
图2 fr =0.08 mm/r 时，钻头进给量随角位移变化图

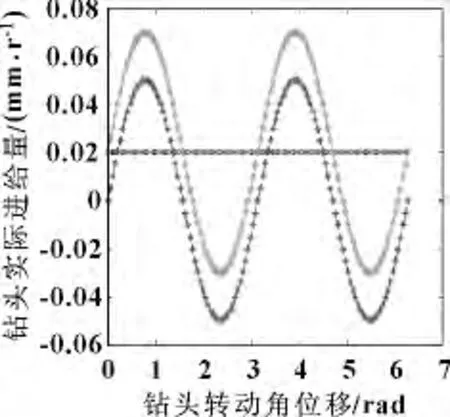
图3 fr =0.02 mm/r 时，钻头进给量随角位移变化图

3 和田玉超声波振动深孔钻削振幅变化特性

3.1 和田玉机超声波振动钻削原理及动力学模型建立

超声波振动深孔钻削系统的工作原理，超声波发生器发出超声频电振荡由振动装置中的换能器接收，换能器将超声频电振荡转化为机械振动，再由振动装置中的变幅杆将换能器转化的机械振动振幅放大，将此放大的机械振动传给所连接的钻杆，从而继续传给钻头，对工件进行钻削加工。

和田玉超声波振动深孔钻削系统在振动加工的振动系统、钻头、工件系统中，由振动机构预设的振幅值，经钻杆传到钻头进行加工。在振动钻削中，振动系统推程段是振幅损失的主要部分，这时钻头压在工件上对工件进行钻削加工，建立数学模型时把处于该状态的振动系统、钻头、工件系统作为一个统一体进行分析。设振动系统、钻头、工件系统的工作端的动态位移为y;由振动系统当量位移即静态位移为yc= Acosωt，根据实际情况把切削系统结构进行简化，由此建立的振动钻削系统的单自由度动力学模型如图4所示。

图中:c 为钻杆阻尼，N·s·m－1;cf为工件阻尼，N·s·m－1;k 为钻杆刚度，N·m－1;kf为工件刚度，N·m－1;m 为系统的质量，kg。

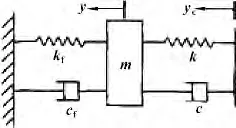
图4 和田玉超声振动钻削动力学模型

3.2 振动钻削运动的微分方程

根据图4 和田玉超声波振动钻削力学模型，由牛顿定律可得:

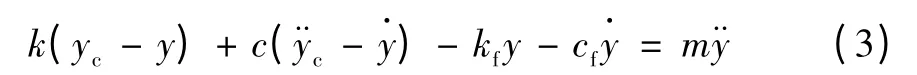
变换后得:

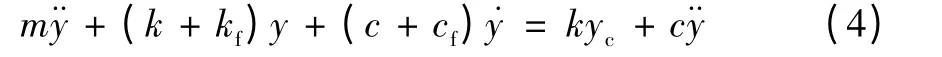
令k+kf=K，c+cf=C

将yc=Acosωt 代入式(4)可得:

式中:m 为系统的质量，kg;A 为振幅，mm;ω 为角速度，rad/s;y 为位移，mm;C 为系统阻尼，N·s·m－1;K 为系统刚度，N·m－1。

3.3 和田玉超声波振动深孔钻削动力学分析

由微分方程的理论知，式(3)的方程解由齐次方程的通解和非齐次方程的特解组成，可以写成如式(4)所示。在振动系统的阻尼作用下，齐次方程的通解与振动钻削系统自由振动对应的暂态振动响应，该振动响应将被衰减，可以对响应值忽略不计。特解可以分成Akcosωt 和Aωcsinωt 的响应总和，即y(t)=y1+ y2。

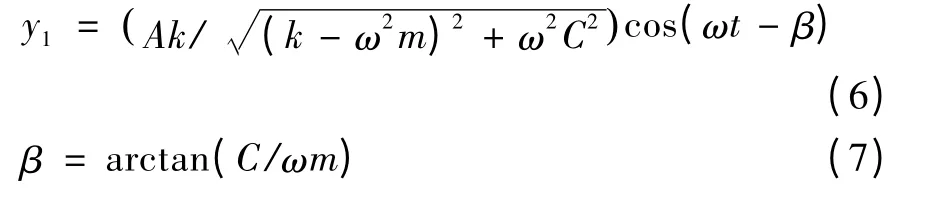
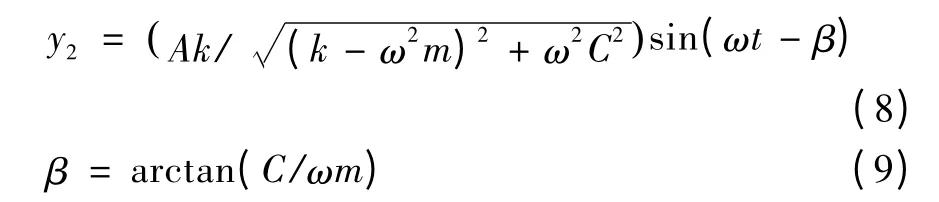
3.4 数值计算与分析

根据上述数学模型，取值A =0.05 mm，m =5 kg，ω = 10 rad/s，C = 0.03 N·s/mm，c = 0.01 N·s/mm不变;在以下两组不同刚度数据下(1)K=500 N/mm，k=100 N/mm;(2)K =200 N/mm，k=50 N/mm 进行振幅损失计算，应用MATLAB 软件计算如图5(a)和图5(b)所示。

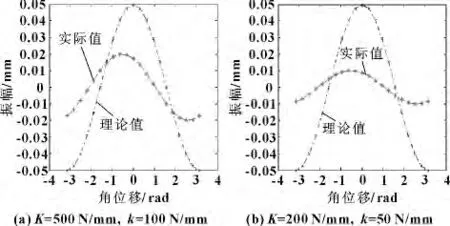
图5 振动损失比较图

根据计算和图形关系曲线可以看出理论振幅要大于实际振幅，在超声振动系统振幅不变的情况下，系统振幅损失量是一样。振幅的损失量与超声振动钻削系统的刚度有密切关系;在保持阻尼不变的情况下，系统刚度值减小，则振幅损失增大。

4 小结

基于和田玉超声波振动深孔钻削工作和结构原理，构建和田玉超声波振动深孔钻削模型;利用在和田玉超声波振动深孔钻削模型分别建立和田玉超声波振动深孔钻削钻削厚度和钻削动力学模型，利用MATLAB 软件进行仿真计算，通过分析计算结果，钻头在一个圆周内的钻削过程中出现空钻现象，出现空钻现象与钻削进给量参数与振动的振幅有关系，钻削进给量小于振动的振幅就会出现空钻现象;振幅的损失量与超声振动钻削系统的刚度有密切关系;在保持阻尼不变的情况下，系统刚度值减小，则振幅损失增大。

［1］王立本，刘亚玲.和田玉、玛纳斯碧玉和岫岩老玉(透闪石玉)的X 射线粉晶衍射特征［J］.岩石矿物学杂志，2002，21(9):62－64.

［2］陈克樵，陈振宇.和田玉的物质组分和物理性质研究［J］.岩石矿物学杂志，2002(Z1):34－39.

［3］黄文.微细深孔超声轴向振动钻削装置的设计［J］.制造技术与机床，2007(9):39－41.

［4］李培繁.超声振动钻削机理实验研究［D］.西安:西安石油大学，2008:13－15.

［5］高本河，熊镇芹，吴序堂，等.振动钻削技术综述［J］.机械制造，2001(1):16－18.

［6］WANG Liping，WANG Lijiang，YANG Zhaojun.Theoretical Investigation and Computer Simulmion of the Dynamic Thrust and Torque in Vibration Drilling［C］//Proceedings of the 6th SJ SUP(C)，1996:573－578.

［7］刘战锋，徐旭松，彭海.高温合金材料的小直径深孔振动钻削试验研究［J］.现代制造工程，2003(9):48－49.

［8］刘战锋，杨立合.深孔超声轴向振动钻削装置的设计与研究［J］.机床与液压，2007(3):56－58.