并联式磁流变阻尼器磁场分布分析

郑佳佳，杨哲，黄林，王炅

(南京理工大学机械工程学院，江苏南京210094)

磁流变液(MR Fluid)作为一种智能材料，依靠其易于控制且连续可控［1］、响应速度快等优点，被应用于许多领域，如航天航空、机电工程、车辆工程、土木工程、医疗、军事工程等［2－8］。基于磁流变技术具有阻尼连续可调、动态范围宽、响应速度快、低功耗等特点，将其应用于反后座装置上，可以减小后坐力和行程，减轻火炮质量，提高机动性能［9－10］。

美国马里兰大学的Norman WERELEY 等设计了基于磁流变减振器的直升机座椅系统，采用半主动控制，振动测试表明传递到座椅上的垂直振动可减小76%［8，11］;英国的Neil D SIMS 等也对应用于飞机起落架上抗冲击的磁流变阻尼器进行了设计、分析和优化［12－13］。

采用传统的串联式阻尼器控制时，各级线圈中同时通过电流并且电流的加载情况是一致的，所以阻尼通道内的磁场分布可以认为是均匀的。新型的级联式阻尼器各级线圈是并联的，每级线圈都可独立工作。当每级单独工作或者多级同时工作时，阻尼通道内的磁场分布是很复杂的，不能再看作单级线圈在理想情况下磁场分布的总和。文中对各种电流加载情况下磁流变阻尼器的磁场分布情况进行分析，根据分析结果总结出适合计算并联阻尼器磁场分布的公式。

1 阻尼器电磁仿真模型的建立

文中所用磁流变阻尼器如图1所示，是单杆长行程磁流变阻尼器，活塞采用四级线圈并联的方式，每级线圈330 匝，允许通过的电流最大值为2 A，其结构为磁路内置、单筒，主要结构包括活塞杆、活塞、缸筒、前后端盖以及充满于缸筒和活塞杆之间的磁流变液组成，其主要尺寸如表1所示。

图1 新型磁流变阻尼器结构示意图

表1 磁流变阻尼器基本参数

整个磁路中磁流变液和45 钢的磁导率都是高度非线性的，为了提高求解计算精度，采用有限元分析法在ANSYS 中来求解电磁场。由于阻尼器是轴对称结构，为了简化计算，取其一个对称面来进行分析，采用轴对称二维静态磁场模块及Plan53 网格单元对新型阻尼器进行有限元建模，如图2所示。

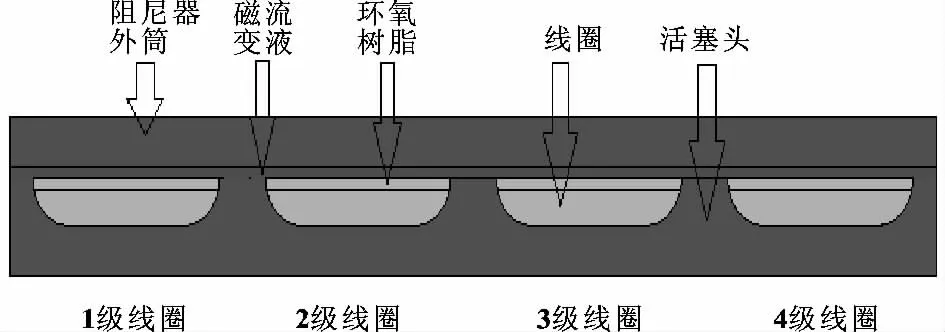
图2 阻尼器有限元模型及线圈编号

活塞与外筒之间留有1.5 mm 的间隙作为阻尼通道，线圈表面和磁流变液之间留有约1 mm 的间隙来填充环氧树脂以防漏磁和腐蚀。根据磁场的磁通连续性定理，近似认为外界无磁通通过，定义磁力线平行与边界。

2 磁场分布仿真

模型建立之后，首先对第1 级线圈单独施加2 A的电流，得到的磁感应强度分布如图3所示。

图3 线圈1 工作时磁感应强度分布图

图3 中5 个高出的波峰对应磁感应强度在5 段有效长度上的分布，可以看出磁感应强度在各段有效长度上都有分布，而不是仅仅分布在通电线圈两侧的有效长度之上。新的级联阻尼器要计算出每级线圈工作时提供的阻尼力的大小，所以分析出每级线圈工作时的磁感应强度分布是关键。

由于阻尼器活塞头结构左右对称，所以第1、2级线圈加载电流时磁感应强度分布分别与第4、3 级左右对称，大小一致。并且由于磁场是矢量，存在方向性，满足磁感应强度同向相加、异向相减原理，所以为得到线圈在任意电流加载下，阻尼通道内的磁感应强度分布情况，只需分析出不同电流作用在第1、2 级线圈时，阻尼通道内的磁感应强度的分布情况。

分别对第1、2 级线圈加载如表2所示8 种大小的固定电流。

表2 第1、2 线圈加载的电流值 A

仿真完成后，为了方便对结果进行分析和比较，在阻尼间隙中间定义路径，提取路径上的磁感应强度分布，并在MATLAB 中把各个电流加载下的磁感应强度分布情况画在一起，得到图4。

图4 单级线圈单独加载时磁感应强度的分布

3 仿真结果分析

分析图4 可知:当电流变化时，磁感应强度在各段有效长度上的变化规律是一致的。所以只需要对其中一段有效长度上磁感应强度与电流的关系进行分析，得出两者的对应关系，就可以把这种对应关系运用到各段有效长度之上。

图4(a)和图4(b)中第二段有效长度上(左侧第二个波峰)磁通量分布幅值较大且均匀，因此选择这段来分析磁通量随电流的变化规律。对第二段有效长度上在不同电流作用下磁感应强度的幅值取平均值，得到表3所示的电流与磁感应强度的对应关系。

对表3 中的数据进行拟合，在精确度为95%条件下，得到磁感应强度B 与电流I 的对应公式，如图5所示。

表3 第二段有效长度上I 与B 的对应关系

图5 单独线圈工作时第二段有效长度上B 与I 的对应关系

式中:I 为电流，单位是A，下标1 表示第1 级线圈上的电流;B 为磁感应强度，单位是T，下标中第一个数字1 代表第1 级线圈加载电流，第二个数字2 代表第2 段有效长度上的磁感应强度，以此类推。

对同一级线圈通电时，电流在各段有效长度上产生的磁通量的变化规律是一致的，只是幅值的大小不同，所以知道其中一段有效长度上的磁场与电流的对应公式后，其余各段有效长度上磁场与电流的对应公式便可通过乘以相应的比例系数得到。当第1 和2 级线圈分别加载电流2 A 时，各段有效长度上的平均磁感应强度如表4所示。

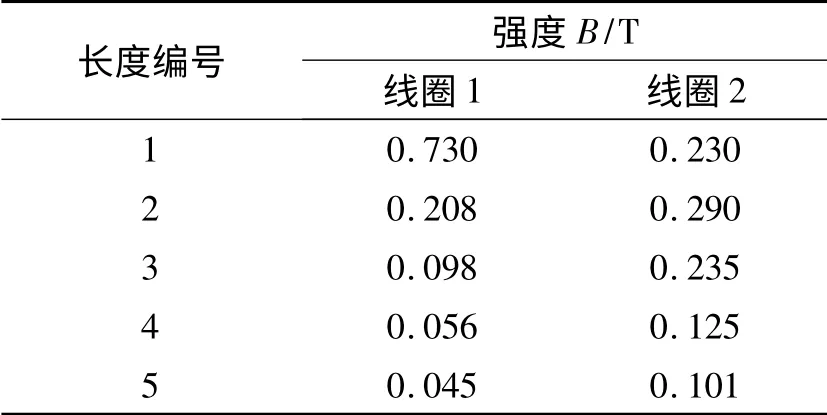
表4 电流为2 A 时各段有效长度上磁通量的幅值

则其余各段有效长度上的公式为:

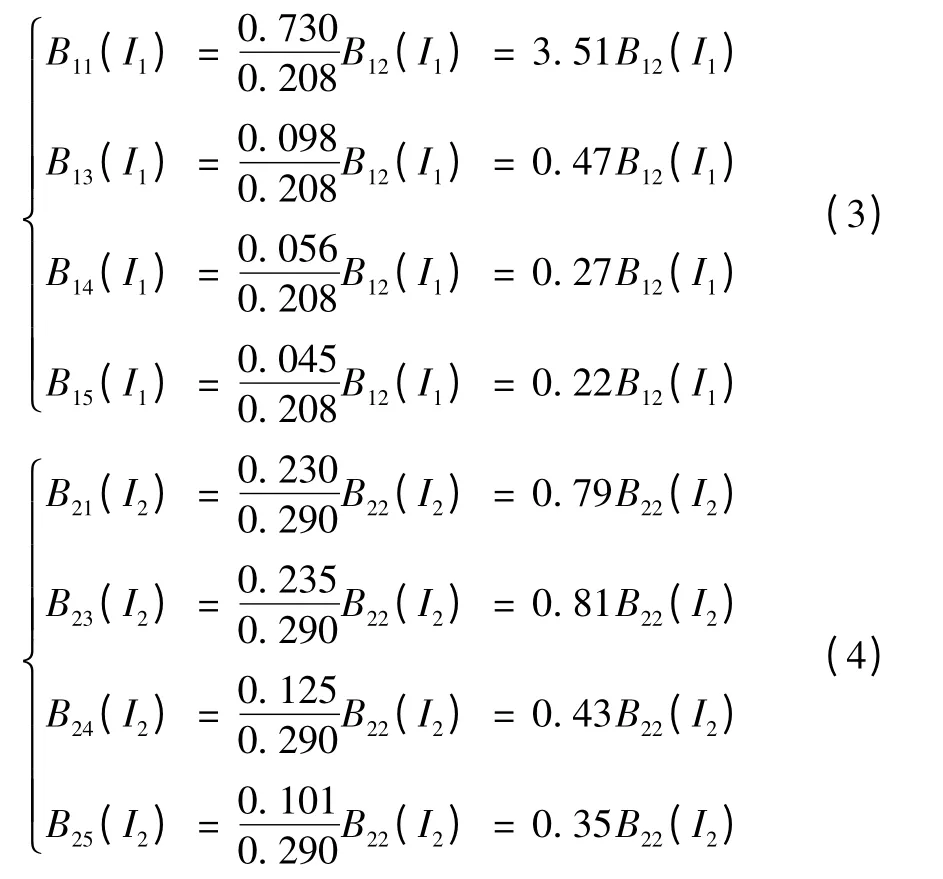
由于磁场是矢量，为了避免相邻两级上线圈产生的磁感应强度叠加抵消，阻尼器工作时相邻两级线圈中的电流方向应该相反。假定阻尼器工作时各级线圈电流的流动方向如图6所示。

图6 阻尼器磁力线方向定义示意图

按图6 方式加载时，各级线圈上的电流在各段有效长度上产生的磁感应强度方向如表5所示。

表5 各级线圈电流在有效长度上的磁感应方向

由公式(1)—(4)、图6 和表5 便可以得出各级线圈在任意电流下磁感应强度在各段有效长度上的分布公式:

其中:Bi(I)(i=1，2，…，5)代表在各级线圈共同作用下，第i 级有效长度上的磁感应强度的大小。假定I1= I4，I2= I3，则B1= B5，B2= B4，式(5)可化简为:

为了在阻尼器结构固定的情况下通过改变电流的大小和方向来减少能耗，应使阻尼通道内单位长度上的等效磁感应强度(Bsum=2B1+4B2+2B3)最大化。在磁路未达到饱和的情况下，当I1=2.26 A，I2=2.5 A(0≤I1≤2.5 A，0≤I2≤2.5 A)，阻尼通道内等效磁感应强度总和取得最大值。即在增加电流的过程中，第一级和第四级线圈所产生的磁回路先达到饱和。Bsum－I 二维曲线如图7所示。

图7 Bsum－I 二维曲线

4 结论

线圈并联的连接方式为改变各级电流大小和方向提供了可能，同时也提高了控制策略的灵活性，有利于达到阻尼器最佳的缓冲减振效果。文中建立了磁流变阻尼器的电磁学模型，并根据仿真结果，对不同电流加载情况下各段有效长度上的磁感应强度分布进行了分析。由分析结果，建立了电流与磁感应强度在任意加载情况下的对应公式，为控制算法的设计奠定了基础。

【1】MARANVILLE C W，GINDER J M.Magnetorhelogical Fluid Damper Dynamics:Models and Measurements［C］//Proc of SPICE，2003:524－533.

【2】MAGANTI G B，SINGH S N，YIM Woosoon.On Absolute Stability and Semi-active Control of a Magnetorheological Fluid Vibration Susppression System［C］//Proceeding of the 18th International Conference on Systems Engineering(ISCEng＇05)，2005:1－6.

【3】KO J M，DUAN Y F，NI Y Q.Modeling of a Full-scale MR Damper and Its Application in Open-loop Vibration Control of Stay Cables［C］// Smart Structures and Materials 2005:Sensors and Smart Structures Technologies for Civil，Mechanical and Aerospace System，2005:690－700.

【4】GONCALVES F D，AHMADIAN M.Behavior of MR fluids at high velocities and high shear rates［C］//Proc of the Ninth International Conference-Electrorheological Fluids and Magnetorheological Suspention，Singapore:World Scientific，2005:412－418.

【5】AHMADIAN M，APPLETON R J，NORRIS J A.Designing Magnetorheological Dampers in a fire Out-of-battery Recoil System［J］.IEEE Transactions on Magnetics，2003，39(12):21－25.

【6】AHMADIAN Mehdi，NORRIS James A.Experimental Analysis of Magnetorheological Dampers when Subjected to Impact and Shock Loading［J］.Communication in Nonlinear Science and Numerical Simulation，2008，13(9):1978－1985.

【7】GONCALVES Fernando D.Characterizing the Behavior of Magnetorhelogical Fluids at High Velocities and High Shear Rates［D］.Virginia Polytechnic Institute and State University，Blackburg，VA，2005.

【8】WERELEY Norman M.Nondimensional Herschel-Bulkley Analysis of Magnetorhelogical and Electrorhelogical Dampers［J］.Journal of Intelligent Material Systems and Structure，2008，19(3):257－268.

【9】张莉洁，王炅，钱林方.冲击载荷下磁流变阻尼器动态特性分析及模型参数辨识［J］.机械工程学报，2009(1):211－217.

【10】WANG Jiong，LI Yancheng.Dynamic Simulation and Test Verification of MR Shock Absorber under Impact Load［J］.Journal of Intelligent Material Systems and Structures，2006，17(14):309－314.

【11】FACEY W B，ROSENFELD N C，CHOI Y T，et al.Design and Testing of a Compact Magnetorheological Damper for High Impulsive Loads［C］//Proceedings of the 9th International Conference on Electrorheological Fluids and Magnetorheological Suspensions，Beijing，China，2004.

【12】BATTERBEE David，SIMS N D.Temperature Sensitive Controller Performance of MR Dampers［J］.Journal of Intelligent Material Systems and Structures，2009，20(3):297－309.

【13】SIMS Neil D，STANWAY Roger，JOHNSON Andrew R.Smart Fluid Damping Shaping the Force/Velocity Response through Feedback Control［J］.Journal of Intelligent Material Systems and Structures，2006，17(4):309－314.