Ø244．5mm套管长圆螺纹接头有限元分析

陈颖杰，邓传光 （中石油西南油气田公司勘探事业部，四川 成都610041）

徐婧源 （中石油西南油气田公司输气管理处，四川 成都610500）

马天寿 （油气藏地质及开发工程国家重点实验室 （西南石油大学），四川 成都610500）

王宇 （中石油西南油气田公司勘探事业部，四川 成都610041）

套管螺纹接头部位是套管连接的薄弱环节，油套管失效事故约64%发生在螺纹连接部位，因此提高套管螺纹的连接质量是确保套管柱质量的关键因素之一［1］。在水平井、大位移井下套管过程中，由于摩阻较大要承受较大的轴向力；由于液柱压力作用要承受较大的内外压力；在弯曲井段要承受弯矩的作用；若旋转套管则要承受扭矩；由于套管接箍上扣扭矩的作用接头还要承受预紧力。因此，研究套管螺纹与接箍螺纹在多种载荷 （轴向力、预紧力、内压、外压、弯矩和扭矩）交互作用下的连接应力、应变问题，对正确选用套管、防止套管螺纹连接失效具有重要的意义［2～4］。通过对Ø244．5mm （9in）套管长圆螺纹接头开展有限元分析，建立了套管螺纹与接箍螺纹接触的力学模型和有限元分析模型，分析了长圆螺纹在复杂载荷综合作用下的应力、应变、接触压力等力学特性。

1 弹塑性接触有限元分析方法

根据变分原理和虚功原理，对于互相接触并产生塑性变形的两个物体，设单元接触边界为Ce，而Ωe和Γe分别为单元面积和单元上作用有面力的边界。则根据虚功方程［5～8］有：

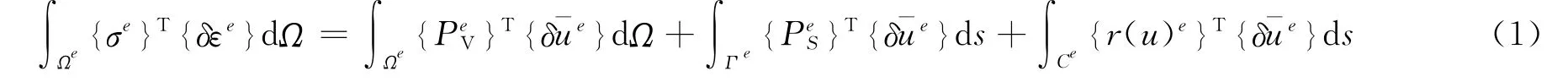
式中：｛σe｝为单元内的应力向量；｛δεe｝为单元内虚应变向量；｛｝为单元的体力向量；｛｝为单元的面力向量；｛｝为单元内虚位移向量；｛r（u）e｝为单元接触边界上的接触力向量；上标T表示转置矩阵。

引入单元形函数 ［Ne］，于是有：

式中：［Ne］为单元形函数；［Be］为单元变形矩阵；［D］为弹性矩阵；｛ue｝为单元位移向量。

由此可推出：

式中：｛（u）e｝为单元的虚功；［K（u）e］为单元刚度矩阵；｛R（u）e｝为单元接触力向量；｛Pe｝为单元载荷向量。

经过对单元方程进行组集可以得到：

对式 （7）进行变形，可得两个相互接触物体系统的弹塑性接触基本方程［5～8］：

式中：｛（u）｝为整体的虚功；［K（u）］为整体刚度矩阵；｛R（u）｝为整体接触力向量；｛P｝为整体载荷向量；｛u｝为位移向量；｛f（u）｝为右端项向量。

根据式 （8）可单独写出两个接触物体的刚度方程式：

式中：［Ki（u）］为物体Ωi的刚度矩阵；｛ui｝为物体Ωi的位移向量；｛Pi｝为物体Ωi的外载向量。

由于接触力向量｛RⅠ（u）｝、｛RⅡ（u）｝未知，使得两个接触物体的刚度方程无法闭合求解，需要补充两个接触物体的接触定解条件和接触状态条件，接触定解和接触状态条件与接触状态有关，接触状态可分为连续、分离、滑动、混合4种情况，具体请参考文献 ［6］。因此，在求解刚度方程式 （9）时，可先假设接触状态，代入相应的定解条件和接触状态条件后，可得：

对上述弹塑性接触问题求解时，一般采用塑性修正迭代方法，这时外载是外载 （体力、面力）、接触点的接触力、支反力等不平衡载荷的叠加，塑性修正迭代过程中外载保持不变，而接触力、支反力在塑性修正迭代过程中不断变化，其变化受位移影响 （位移的改变将导致接触状态和接触力发生改变，而接触状态和接触力又会反过来影响位移），因此需要通过将接触力、支反力嵌套在外层循环中的内层循环方可迭代求解。此处采用修正的Newton-Raphson法进行求解，其迭代格式为［5～8］：

式中：｛Δu（n）｝为n次迭代的位移增量；［KT（u（0））］为切线刚度矩阵；｛Ψ（u（n））｝为非平衡力向量；｛σ（n）｝为应力向量；｛ΔR（Δu（n））｝为接触力增量向量；｛u（n）｝为n次迭代的近似解；n为迭代步数。

由弹塑性接触方程和塑性修正迭代格式可知，迭代过程中涉及3个层面的循环，包括内层的接触迭代、中间层为塑性修正迭代、外层为增加加载迭代，这种方法可用于求解空间轴对称、平面应变和平面应力情况下的弹性或弹塑性接触问题。这种方法也可求解单个连续体的弹塑性问题，还可以求解多个物体接触的弹塑性问题［6］。

2 力学分析模型及边界条件

考虑到Ø244．5mm套管长圆螺纹接头在空间结构上轴对称，为此将Ø244．5mm套管螺纹与接箍螺纹接触的力学模型简化为轴对称模型。如图1（a）所示，图中给出了套管螺纹接头所承受的各种载荷，包括预紧力、轴向力、内压、外压、弯矩和扭矩。在力学模型的基础上，依据P110钢级的Ø244．5mm×11．99mm套管结箍螺纹尺寸建立长圆螺纹接头的几何模型，通过划分网格建立了套管长圆螺纹接头有限元模型，如图1（b）所示，网格划分采用了四边形单元，其中套管螺纹与接箍螺纹啮合面采用接触单元划分［9，10］，所建立的长圆螺纹接头有限元模型中有25个螺牙接触面，50个接触节点。套管螺纹接头的材料参数为：弹性模量E＝2．01×105MPa，泊松比ν＝0．29，屈服强度σs＝758．42MPa，拉伸强度σb＝965MPa，摩擦因数μ＝0．055。

套管偏梯形螺纹接头有限元模拟分析时还需要考虑载荷条件及边界条件，在套管接箍 （母接头）中间对称面为轴向固定约束边界条件，在有限元模型的上端套管本体上端面施加预紧力、轴力、内外压力、弯矩和扭矩等载荷，分析中可采用叠加原理，分别模拟单一载荷下的受力特性然后叠加到一起。套管上承受的各种载荷在有限元模型中加载方式如下：

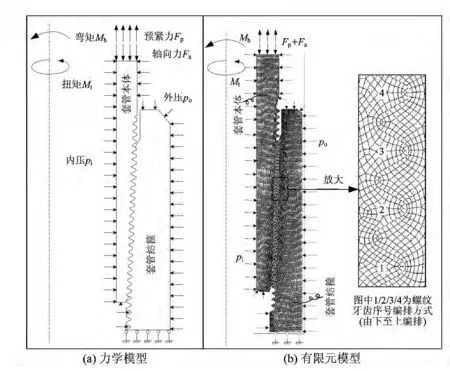
图1 套管长圆螺纹接头不同载荷下的力学模型

1）预紧力 加载在套管上的预紧力实际上是预紧力矩 （扭矩），为此通过在套管本体上加载轴向力代替预紧力矩，套管螺纹的预紧力矩可以换算成轴向分布力Fp作用于套管本体的上端面［5］：

式中：Fp为预紧力，kN；T为上扣扭矩，kN·m；d2为螺纹中径，m；φ＝arctan为螺纹升角，（°）；φv＝arctanfv为螺旋副当量摩擦角，（°）；fv＝0．15；Do为套管外径，m；di为套管内径，m。

2）轴向力 通过施加相当载荷的方法将轴向力换算成轴向应力Fa作用于套管本体上端面，其大小为：

式中：Fa为轴向应力，MPa；F为轴向力，kN。

3）内外压力 内外压力是指钻井液液柱压力，内外压力直接作用在与流体湿接触的任何部位，加载时可直接在套管本体、接箍的内外表面加载均布压力，注意内表面加载内压pi、外表面加载外压po。

4）弯矩和扭矩 弯矩Mb和扭矩Mt是非轴向对称载荷，利用有限元法处理，需要进行Fourier变换，即可以将作用在轴对称体上的任意不对称载荷展成Fourier级数［6，7］，从而将载荷参数沿某一坐标方向展成级数，这些参数在该坐标方向用解析函数表示，而在另外两个方向仍然采用一般有限元方法即可求解。

3 有限元模拟结果及分析

分别对Ø244．5mm长圆螺纹接头套管的上扣、下套管、模拟旋转3种典型作业工况下的螺纹牙齿受力、应力和应变开展分析和研究，以揭示Ø244．5mm套管长圆螺纹接头的力学特性。模拟上扣、下套管、旋转套管3种典型工况下的加载方式如下：①模拟上扣 （工况1）：施加预紧力矩15kN·m和轴向力100kN以模拟上扣结束时的工况；②模拟下套管 （工况2）：施加预紧力矩15kN·m、轴向力100kN、内压15MPa、外压10MPa；③模拟旋转套管 （工况3）：施加预紧力矩15kN·m、轴向力100kN、内压15MPa、外压10MPa、弯矩10kN·m、扭矩5kN·m。

3.1 螺纹牙齿接触压力分析

图2所示为Ø244．5mm套管长圆螺纹接头在上扣、下套管、旋转套管3种典型工况的各牙齿接触压力对比分布图，图示牙齿序号的编排方式参见图1（b）有限元网格模型中自下而上的螺纹牙齿序号编排方式。不难看出，3种工况下牙齿的接触压力在前4颗牙齿处比其他牙齿大很多，3种情况下的接触压力分布情况基本类似，分布规律也基本一致，接触压力曲线总体上呈 “L”形状，即牙齿最大接触压力变化趋势是先急剧降低后趋于平稳最后又略有增加，即在最后3颗牙齿处的接触压力略有增加。其中，上扣时螺纹牙齿的最大接触压力为177．0MPa，平均接触压力为46．1MPa；下套管时螺纹牙齿的最大接触压力为263．5MPa，平均接触压力为60．9MPa；旋转套管时螺纹牙齿的最大接触压力为307．2MPa，平均接触压力为72．9MPa。3种情况中旋转套管时牙齿的接触压力最大，上扣时牙齿的接触压力最小，下套管介于中间。在前4颗牙齿处，由于接触压力较大，在过载的情况下，容易引起粘扣等失效事故的发生。

3.2 螺纹牙齿位移场分析

图3所示为3种典型工况下Ø244．5mm套管长圆螺纹接头螺纹牙齿的最大位移对比分布图。不难看出，3种情况下牙齿的最大位移在前5颗牙齿处比其他牙齿大一些，3种情况下的接触压力分布情况基本类似，分布规律也基本一致，牙齿的最大位移曲线总体上呈下降变化趋势，即牙齿的最大位移变化趋势随牙齿序号增加缓慢降低。3种情况下牙齿的最大位移分布总体上比较均匀，旋转套管时牙齿的位移最大，上扣时牙齿位移最小，下套管时介于二者之间。其中，上扣时螺纹牙齿的最大位移为0．083mm，平均位移为0．749mm；下套管时螺纹牙齿的最大位移为0．124mm，平均位移为0．108mm；旋转套管时螺纹牙齿的最大位移为0．148mm，平均位移为0．128mm；Ø244．5mm套管长圆螺纹牙齿的最大位移以轴向应变为主，径向应变和环向应变均比较小，而环向应变主要是由于扭矩作用产生的。

图2 3种工况下螺纹牙齿接触压力分布

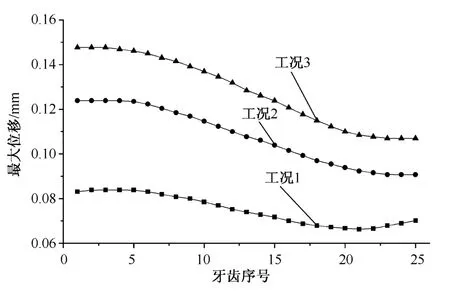
图3 3种工况下螺纹牙齿最大位移分布

3.3 螺纹牙齿应力场分析

图4 所示为3种工况下Ø244．5mm套管长圆螺纹接头螺纹牙齿的最大Von Mises等效应力对比分布图，图5所示为3种工况下Ø244．5mm套管长圆螺纹接头螺纹牙齿Von Mises应力分布。可以看出，3种工况下牙齿的Von Mises等效应力在前3颗牙齿处比其他牙齿大很多，在最后3颗牙齿处的Von Mises等效应力也比中间的其他牙齿略高；3种情况下牙齿的最大Von Mises等效应力分布情况基本类似，分布规律也基本一致，牙齿的最大Von Mises等效应力曲线总体上呈 “L”形状，即牙齿最大接触压力变化趋势是先急剧降低后趋于平稳最后又略有增加。其中，工况1螺纹牙齿的最大Von Mises等效应力为302．7MPa，平均为132．2MPa；工况2螺纹牙齿的最大Von Mises等效应力为357．8MPa，平均为174．1MPa；工况3螺纹牙齿的最大Von Mises等效应力为452．0MPa，平均为214．5MPa。3种情况中工况3牙齿的Von Mises等效应力是最大的，工况2介于中间，工况1最小。在前4颗牙齿处，由于最大Von Mises等效应力普遍较高，在过载的情况下，容易引起粘扣等失效事故的发生。

图5 3种工况下螺纹牙齿Von Mises应力分布

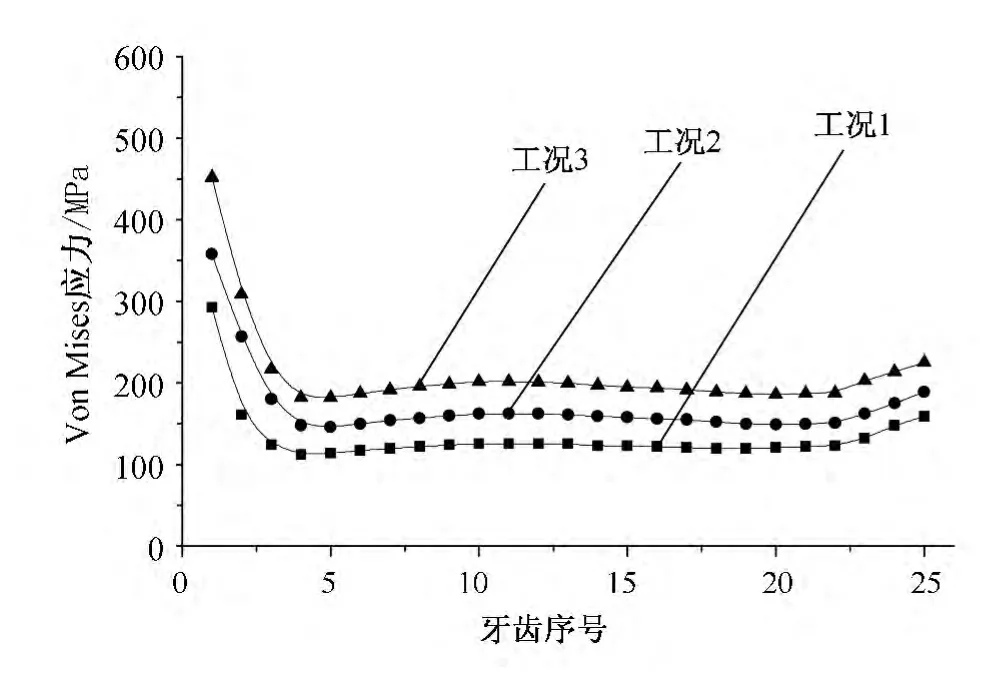
图4 3种工况下螺纹牙齿最大Von Mises等效应力分布

4 结论

1）基于变分原理和虚功原理，推导了2个物体接触的弹塑性接触基本方程，分析了弹塑性接触问题的求解方法，得出了采用修正的Newton-Raphson法进行求解的迭代格式，建立了套管螺纹接头进行弹塑性接触有限元分析的理论方法。

2）根据Ø244．5mm套管长圆螺纹接头的实际工作情况，建立了Ø244．5mm套管长圆螺纹的轴对称力学模型和接触有限元分析模型，研究了接触有限元分析模型中预紧力、轴力、内压、外压、弯矩和扭矩等载荷的加载方式，形成了系统的套管长圆螺纹接头接触问题的分析方法。

3）采用接触有限元分析方法研究了Ø244．5mm套管长圆螺纹在模拟上扣、下套管、旋转套管等典型工况下的力学特性，得到了螺纹牙齿承受的接触压力、位移、Von Mises应力分布规律。结果表明：3种典型工况下长圆螺纹牙齿的接触压力、Von Mises应力和位移的分布规律基本一致；长圆螺纹牙齿上承受的最大接触压力和最大Von Mises应力分布曲线总体上呈 “L”形状，即变化趋势是先急剧降低后趋于平稳最后又略有增加，在前3颗啮合牙齿上作用的Von Mises应力和接触压力都很大，螺纹连接在该部位容易失效；螺纹牙齿最大位移分布规律呈现出逐渐降低的趋势，即靠近最下端的螺纹压力变形最大。

［1］袁光杰，林元华，姚振强，等 ．API偏梯形套管螺纹连接的接触应力场研究 ［J］．钢铁，2004，39（9）：35～38．

［2］王树平，陈平，石晓兵，等 ．温度对套管接头螺纹接触压力的影响 ［J］．西南石油学院学报，2005，27（4）：63～65．

［3］王琍，张汝忻，刘玉文，等 ．API套管圆螺纹接头粘扣失效分析 ［J］．钢铁，2000，35（5）：44～47．

［4］齐俊林，罗维东，张宏，等 ．圆螺纹套管接头上扣与滑脱数值模拟 ［J］．石油大学学报，1998，22（4）：68～71．

［5］林腾蛟，蒋仁科，李润方，等 ．Ø139．7mm大尺寸偏差油管螺纹接头弹塑性接触特性研究 ［J］．机械科学与技术，2007，26 （8）：992～995．

［6］李润方，李剑霞 ．接触问题数值方法及其在机械设计中的应用 ［M］．重庆：重庆大学出版社，1991．14～16．

［7］林元华，施太和，赵鹏，等 ．复杂地层钻具接头力学性能模拟及应用 ［J］．钢铁，2005，40（8）：43～47．

［8］李润方，林腾蛟，唐倩，等 ．石油钻杆联接螺纹弹塑性接触有限元分析 ［J］．石油矿场机械，1998，27（6）：44～46．

［9］陈颖杰 ．Ø244．5mm套管偏梯形螺纹接头有限元分析 ［J］．石油矿场机械，2013，42（10）：40～44．

［10］练章华，韩建增，张毅，等 ．套管偏梯形和圆形螺纹滑脱载荷分析 ［J］．石油机械，2004，32（5）：7～9，49．