宁波市地下水位动态与地面沉降预测分析＊

付延玲

（河海大学地球科学与工程学院，南京 210098）

宁波市是我国著名的港口城市和历史文化名城，位于浙江省东部，长江三角洲东南角，浙江宁绍平原东端，东临东海，北濒杭州湾，西接绍兴市，南接三门湾，东西宽175km，南北长192km。区内从上往下分布的第四纪松散孔隙含水层有全新统的潜水含水层、上更新统第Ⅰ承压含水层（可划分为上下两个含水层I1、I2）和中更新统第II承压含水层，各含水层之间均以弱含水的黏性土层相分隔，是我国第四纪孔隙承压水开发利用最早的城市之一。上世纪六十年代以来，随着工农业的快速发展，深层孔隙承压水开采量剧增，造成区域地下水位急剧下降，地下水资源衰竭、水质恶化，引发了严重的地面沉降问题，并有进一步扩大的趋势。为此，宁波市政府为了有效地控制地面沉降的进一步发展，从2008年底起对第四纪孔隙承压水实行全面禁采，孔隙承压水水位得到了有效控制，并日趋回升。

为了查明禁采后地下水位的动态变化趋势及对地面沉降的控制效应，本文将宁波市第四纪松散沉积层作为一个统一的水文地质体，在概化出宁波市第四纪松散沉积层地下水系统水文地质概念模型的基础上，建立了宁波市第四纪松散沉积层地下水系统三维数值模拟模型和地面沉降与地下水位多元线性回归模型［1－2］，在对各含水层及相应黏性土弱含水层地下水位进行模拟预测的同时，模拟预测了由各含水层及相应黏性土弱含水层地下水位变化引起的地面沉降问题，为宁波市地面沉降防治规划的确定提供了科学依据。

1 研究区地下水系统水文地质概念模型

本次模拟计算将宁波市第四纪松散沉积层作为一个统一的地下水系统，平面上北部以江北区与镇海区行政交接边界为界，东部以鄞州区与北仑区行政交接边界为界，东南部以第四系边界为界，西南部以鄞州区与奉化市行政交接边界为界，西部以第四系边界为界，四周均概化为通用水头边界，计算面积共约835km2，包括了海曙区、江东区、江北区全区及鄞州区平原部分。剖面上自上往下，包括潜水含水层、浅部承压含水层、第I1、第I2承压含水层和第II承压含水层，以及各含水层之间的黏性土弱含水层，各层均概化为非均质各向异性（图1）。系统顶部一方面接受大气降水的补给，为补给边界；另一方面地下水又通过其蒸发及植物的蒸腾，是一排泄边界。系统的底部接受下伏基岩水的补给，是一补给边界。地下水流态概化为三维非稳定流。区内地下水的开采量根据统计资料，分别按单井及以乡镇为单位的大井处理。

图1 宁波市水文地质剖面图Fig．1 Hydrogeological section of Ningbo City

2 数学模型

根据上述研究区地下水系统的水文地质概念模型，取坐标轴方向和含水层主渗透方向相一致，可建立下列与之相适应的地下水运动三维非稳定流数学模型［3］

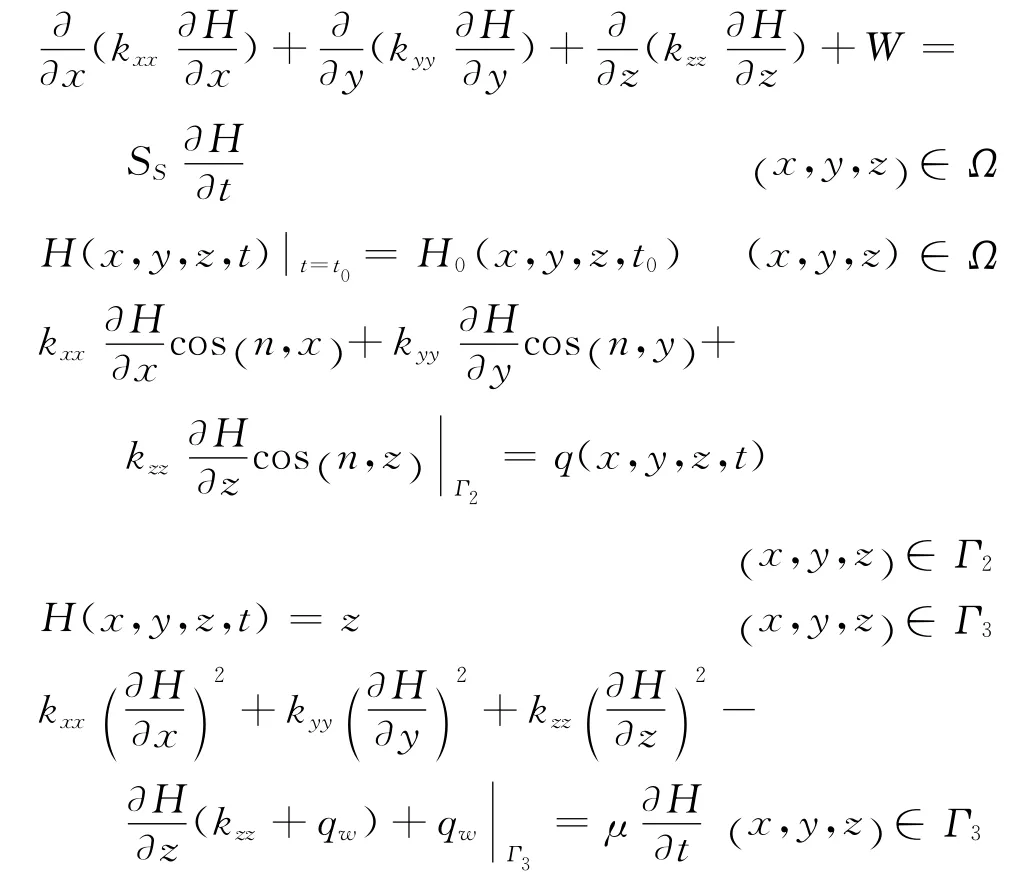
式中：

kxx、kyy，、kzz分别为含水层各向异性主方向渗透系数（m／d）；

H为点（x，y，z）在t时刻的水头值（m）；

W为源汇项（1／d）；SS为贮水率（1／m）；

t为时间（d）；Ω为立体计算域；

H0（x，y，z，t0）为点（x，y，z）处的初始水位（m）；

cos （n，x） 、cos （n，y） 、cos （n，z） 分别为各向流量边界外法线方向与坐标轴方向夹角的余弦；

q（x，y，z，t）为第二类边界上单位面积的侧向补给量（m／d）；

μ为饱和差（自由面上升）或给水度（自由面下降），它表示在自由面改变单位高度下，从含水层单位截面积上吸收或排出的水量；

qw为自由面单位面积上的大气降雨入渗补给量与地下水蒸发量之和（m／d）；

Γ2、Γ3分别为第二类边界和自由面边界。

3 模型的识别、验证

上述模型采用有限差分法求解［4－5］，并采用强隐式（SIP）联立迭代求解代数方程组［6］。将整个研究区在平面上剖分成250×250个矩形网格单元，单元边长为270×268m。垂向上按潜水含水层、浅部孔隙承压含水层、第I1、第I2承压含水层、第II承压含水层及各含水层之间的黏性土弱含水层进行剖分，共分9层。每层的有效计算单元为11977个，共计107793个，详见图2。以2008年12月31日至2009年12月31日作为模型识别、验证的时段，一个月为一个应力期，共分为12个应力期，每个应力期又分为10个计算时间步长。

地下水系统各含水层均有一定数量的地下水位监测井用来进行水位拟合，共计76个，基本上控制了各含水层地下水流场。各含水层的初始流场均由实测水位经Kriging插值给出，各含水层之间的黏性土弱含水层初始流场由上下含水层初始流场插值获得，图3为第II承压含水层初始流场图。2009年各含水层开采量由实际统计给出。各含水层及之间的黏性土弱含水层通用水头边界上的水头值由实测值经插值给出。各含水层及之间的黏性土弱含水层参数分区的参数初值均按实验分析、前人资料并结合经验给出［7－8］。图4和图5为第II承压含水层各监测井2009年6月30日和12月30日的地下水位拟合精度，水位拟合误差均在1m 以下。

图2 研究区剖面图Fig．2 Section maps of studied area

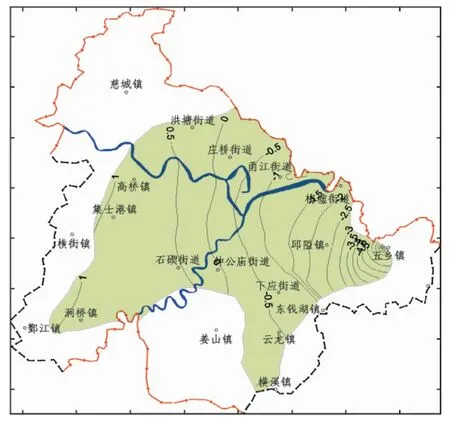
图3 第Ⅱ承压含水层2008年12月31日初始流场（单位：m）Fig．3 Initial flow fields of confined aquiferⅡon December 31st，2008

图4 第Ⅱ承压含水层2009年6月30日地下水位拟合图Fig．4 Fitting of groundwater levels of confined aquifer Ⅱon June 30st，2009

经识别、验证，得出了各层的渗透系数和储水率等参数分区及其各分区的参数值。其中：潜水含水层共分6个参数区，水平渗透系数为3×10－6～1×102m／d，垂向渗透系数为7×10－7～40 m／d，给水度为1．54×10－5～3×10－1；浅部孔隙承压含水层共分3个参数区，水平渗透系数为5×10－4～60m／d，垂向渗透系数为1×10－5～5m／d，弹性储水率为1×10－4～2×10－3m－1；第I1、第I2承压含水层共分19个参数区，水平渗透系数为5×10－1～25 m／d，垂向渗透系数为1×10－2～2m／d，弹性储水率为1×10－8～2×10－5m－1；第II承压含水层共分18个参数区，水平渗透系数为1×10－2～30m／d，垂向渗透系数为1×10－3～3m／d，弹性储水率为5×10－8～3×10－4m－1；浅层黏性土弱含水层共分5个参数区，水平渗透系数为8×10－7～80m／d，垂向渗透系数为8×10－8～8m／d，弹性储水率为1×10－8～2×10－3m－1；第I黏性土弱含水层（I1、I2间黏性土隔水层分布不稳定）分为1个参数区，水平渗透系数为5．0×10－5m／d，垂向透系数为1．5×10－6m／d，弹性储水率为1．0×10－6m－1；第II黏性土弱含水层也分为1个参数区，水平渗透系数为1．5×10－4m／d，垂向渗透系数为1．5×10－5m／d，弹性储水率为1．0×10－8m－1。图6为第II承压含水层水文地质参数分区特征，表1为第II承压含水层的水文地质参数值。

图5 第Ⅱ承压含水层2009年12月30日地下水位拟合图Fig．5 Fitting of groundwater levels of confined aquifer Ⅱon December 30st，2009

图6 第Ⅱ承压含水层水文地质参数分区图Fig．6 Division map of hydrogeological parameters of confined aquiferⅡ

表1 第Ⅱ承压含水层水文地质参数分区值Table 1 Division values of hydrogeological parameters of confined aquiferⅡ

从识别结果来看，地下水系统各参数分区参数值的级别大小均符合常规，边界上的水量交换强弱程度和实际基本一致，较好地反映了宁波市第四纪松散沉积层地下水系统的结构与功能特征。各监测井水位计算值和实测值拟合程度也较好，说明模型计算所得结果正确、可信，可以用来预测宁波市第四纪松散沉积层地下水位的动态变化。

4 地下水位动态预测

保持2009年的开采量和开采布局，以2009年12月31日作为预测初始时刻，预测2009年12月31日至2020年12月31日逐月的地下水流场变化特征。

预测结果表明：山区沟谷孔隙潜水地下水位降落漏斗逐渐扩大，至2020年12月底，如凤岙水厂开采形成的地下水位降落漏斗中心水位标高为－3．4m，鄞江水厂、镇电集水厂开采形成的地下水位降落漏斗中心水位标高为0．0m。平原区潜水水位年内变化随大气降水量变化而变化，总体上水位基本处于稳定；山前浅部孔隙承压水动态变化与潜水基本一致，平原区浅部孔隙承压含水层水位年际变化不大，地下水流场年际变化不明显；全区深层孔隙承压水水位降落漏斗恢复较快，第I1与第I2承压含水层地下水位降落漏斗在2010年4月之后即已恢复，2010年6月第II承压含水层降落漏斗恢复。深层孔隙承压水水位年际变化不大，年内水位一般4月到8月份水位较低，9月到次年3月水位较高。图7 和图8为第II承压含水层2012年12月31日和2020年12月31日的地下水预测流场，可见，2012年后深层孔隙承压水的地下水流场基本稳定，年际变化不大，第I、第II承压含水层位于市区的地下水位降落漏斗也均已得到恢复。

图7 第Ⅱ承压含水层2012年12月31日预测流场（单位：m）Fig．7 Forecast flow fields of confined aquiferⅡon December 31st，2012（unit：m）

5 地面沉降动态预测

（1）地面沉降量与地下水位变化的多元线性回归模型

根据太沙基有效应力原理，土体压缩变形量与孔隙水压力的变化量存在线性相关关系［9］，由此可以推断含水层的压缩沉降量与地下水位变幅存在线性相关关系［10］。根据宁波市江东北路监测点1985年至2008年各含水层及之间的黏性土弱含水层的月压缩沉降量与相应的月水位变幅数据，采用多元线性回归方法，建立地面沉降量与各含水层及之间的黏性土弱含水层地下水位变幅的多元线性回归模型：

Δb＝a0＋a1ΔH1＋a2ΔH2＋a3ΔH3＋a4ΔH4＋a5ΔH5＋a6ΔH6

其中：

Δb为月地面沉降量（mm）；

ΔH1为潜水月水位变幅（m）；

ΔH2为浅部孔隙承压含水层月水位变幅（m）；

ΔH3为浅部孔隙承压含水层与第Ⅰ承压含水层间黏性土弱含水层月水位变幅（m）；

ΔH4为第Ⅰ承压含水层月水位变幅（m）；

ΔH5为第Ⅰ承压含水层与第II承压含水层间黏性土弱含水层月水位变幅（m）；

图8 第Ⅱ承压含水层2020年12月31日预测流场（单位：m）Fig．8 Forecast flow fields of confined aquiferⅡon December 31st，2020（unit：m）

ΔH6为第II承压含水层月水位变幅（m）；

a0为常数项，与各含水层和黏性土弱含水层的监测控制程度和监测精度及非地下水开采引起的地面沉降有关；

a1、a2、a3、a4、a5、a6为系数项，与各含水层和黏性土弱含水层的骨架释水系数有关。

根据已有266 组因变量（月沉降量）与自变量（各层月水位变幅）观测统计数据，经计算得到了下列多元线性回归方程：

Δb＝－0．856＋1．222ΔH1＋0．457ΔH2＋2．605ΔH3＋0．319ΔH4＋0．626ΔH5＋0．832ΔH6

上述模型经拟合度检验分析、方差分析，共线性检验分析和残差分析［11］可知，模型正确可信，可以用来预测地面沉降的发展趋势。

（2）地面沉降量预测

应用上述地下水系统数值模型，预测得到了江东北路监测点各含水层及之间的黏性土弱含水层2010至2020年的月水位变幅值，再利用上述地面沉降与地下水位变化的多元线性回归模型，预测得到了逐月的地面沉降量，在此基础上，经累计获得了2010年至2020年的年地面沉降量，详见表2。

表2 2010年至2020年地面沉降量预测（mm／a）Table 2 Prediction of land subsidence rates from 2010to 2020（mm／a）

由上述计算结果可知，宁波市江东北路监测点2012年后年地面沉降量逐年减小，主要是因为2012年后各含水层及之间的黏性土弱含水层地下水位趋于稳定，由地下水位下降引起的地面沉降均基本得到控制。

6 结论

（1）本次模拟计算将宁波市第四纪松散沉积层作为一个统一的地下水系统，采用真三维数值模型，分别建立了各含水层和黏性土弱含水层的地下水流动方程，并通过垂向渗透系数发生水力联系，克服了以往二维和准三维模型将相邻含水层之间的黏性土弱含水层概化为越流层给模拟计算带来重复或缺失的不足，提高了模拟计算的精度。

（2）宁波市2012年后各含水层及之间的黏性土弱含水层地下水位趋于稳定，地面沉降量逐年减小，由地下水位下降引起的地面沉降均基本得到控制。

［1］薛禹群，谢春红．地下水数值模拟［M］．北京：科学出版社，2007：1－50．

［2］黄丹，肖伟，李勇．地下水三维数值模拟及其优化开采［J］．资源调查与环境，2005，26（2）：137－145．

［3］付延玲．基于地面沉降控制的区域性松散沉积层地下水可采资源规划评价［J］．吉林大学学报（地球科学版），2012．42（2）：476－484．

［4］孙从军，韩振波，赵振，等．地下水数值模拟的研究与应用进展［J］．环境工程，2013，31（5）：9－17．

［5］Wang Kun，Jin Scheng，Liu Gang．Numerical modeling of free－surface flows with bottom and surface－layer pressure treatment［J］．Journal of Hydrodynamics，2009，21（3）：352－358．

［6］PATRICKL A．Natural disasters［J］．Surficial Geology，1996，21（3）：34－36．

［7］吴天寿，叶俊能．宁波轨道交通水文地质参数试验及工程应用［J］．宁波大学学报，2013，26（3）：127－132．

［8］许烨霜，余恕国，沈水龙，等．地下水开采引起地面沉降预测方法的现状与未来［J］．防灾减灾工程学报，2006，26（3）：352－356．

［9］ZHANG Yun，XUE Yu－qun．WU Ji－chun，et al．Land subsidence and earth fissures due to groundwater with－drawl in the Southern Yangtze Delta，China［J］．Environmental Geology 2008，55（4）：751－762．

［10］贾莹媛，黄张裕，张蒙，等．含水组地下水位变化对地面沉降影响的多元回归分析与预测［J］．工程勘察，2013（1）：77－80．

［11］袁志发，周静芋．多元统计分析［M］．北京：科学出版社，2002．