信息的编码：四位二进制编码

吴俊杰

主持人手记：本专栏主要介绍信息技术实验在基础教育信息技术课当中的典型案例，并期望这些案例能够促进信息技术课程学科合法性的提升、丰富信息技术课的教学内容、拓展信息技术教师的课程设计视野。对此栏目有任何好的主意或建议，请发送稿件至towujunjie@163.com（主持人）或tougao1@chinaitedu.cn（杂志社）。

我们知道，二进制的基础是二值量，一个二值量可以表示两种状态，两个独立的二值量可以表示2×2=4种状态，n个独立的二值量可以表示2n种状态。如果想将这些状态和现实生活中需要测量或者控制的状态结合起来，就需要对其进行编码，将每种状态和一种现实需要的计算机的输入或输出状态对应起来。例如，我们用二值量状态表示不同的音符，则至少需要3个独立的二值量，其8种状态的7个状态表示从do ～xi之间的7个音符，而这8种状态如何和7个音符一一对应起来则是一个编码的过程，像这种将二值量的状态和需要用二值量表述的信息一一对应起来的过程，我们称为信息的编码。在本章，我们将研究二值量的编码的规律。

● 确定一组独立二值量的编码空间

独立的两个二值量是指他们之间可以彼此独立地改变状态，如键盘上的两个键，一个键按下并不会影响另一个键的状态，它们是彼此独立的，但如果将两个键用一根木杆粘接起来，它们彼此之间就不再独立了。

在Scratch传感器板中，端口A、B、C、D是四个独立的二值量，它们各自的两种状态放置到图1所示的如果的条件判断当中，不同的组合就构成了不同的状态。

我们将LabPlusTMScratch传感器板的四个按键接入A～D四个端口上（如图2），四个按键便可控制四个端口的逻辑值。

当然，我们可以通过复杂的逻辑关系，写一个非常长的逻辑表达式来表述不同的状态，但此次我们用0表示按键弹起（默认状态），1表示按键按下，以ABCD的次序来建立一个0和1构成的字符串，这个四位的字符串，用变量表示（如下页图3），用来侦测当前状态。

按下空格之后，任意按下这四个按键的一种组合，程序会记录当前的状态到变量中，当然我们可以使用枚举的方法列出这16种状态，也可以发挥计算机的优势，即我们用一个链表来保存所有的状态，接下来随机地“乱按”出一种状态，让计算机判断该状态是否是一个之前没有发现的状态，并判断是否要放在 链表中（如图4）。

很快16种状态就采集完成了，如果我们现在有一个简单的需求，即用二进制的组合表示0～9这10个数字，状态空间中状态的数目16已经能够满足将0～9这10个数字一一对应起来的要求，下一步就需要建立一种对应规则，即编码。

● 将二值量和需要描述的信息对应起来

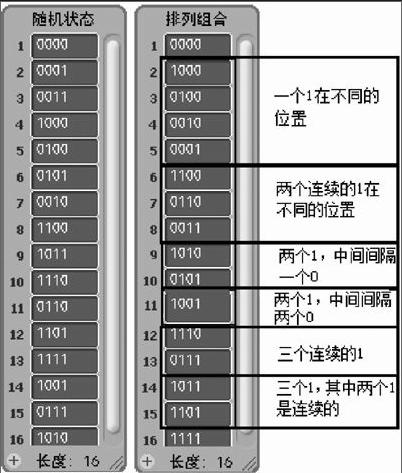
图5左图的链表表示的是随机生成的16种状态，这16种状态的枚举是没有规律的，大概通过100次的随机按键，会把这16种状态收集齐全，状态数目越多，越难以通过枚举的方法得到所有状态。因此，图5右图所示使用的排列组合方法，依据一些规律，能找到这16种状态，但是这种方法的效率仍然不够高。无论是随机组合得到的16种状态，还是用排列组合的方法得到的16种状态，我们都可以挑选前10种状态和需要表述的0～9的数字相对应。

考虑到在没有任何按键按下时，系统的默认状态为0000，因此默认状态不加入编码，将图5右图的状态与0～9的数字对应，得到了表1所示的编码表，至此初步完成了编码的过程。

表1的结论说明至多使用四个按键当中的两个，我们就可以独立表示出10个不同的信息，根据编码表我们可以将当前状态转化为十进制数输出。我们使用如下页图6所示的广播，就可以将用四个按键的组合输出0～9所表示的数字。

但是如果做实验会发现当输入数字4的时候，即按键A和按键B同时按下，有时系统最终显示的可能是0或者1，这是因为，松开按键的瞬间，有可能按键A比按键B后松开，系统会认为，只有A按下，因此认为当前状态为1000，输出0，同理有可能输出1，这个问题我们会在之后的文章中解决。

● 二进制和十进制之间的转化

用枚举的方法得到所有状态虽然比较容易理解，但是当要处理的二值量的数目增多，即状态的位数增多后，我们将会越来越难以枚举所有状态，因此有必要用更加科学的方法将所有状态表示出来。首先，让我们回顾一下十进制的情况，假设A、B、C、D四个端口每个端口都有0～9共10种状态，那么它们的组合自然是从0000～9999这10000种状态，我们获取每个状态的方法是，从最小的状态0000开始，每次给当前状态加1，当我们加9次1得到状态0009之后，我们需要运用进位法则即当当前位已经为最高位9的时候，需要将当前位归0，之后，将上一位加1。运用类似的规则，我们发现二进制的最高位为1，即0001再加1之后，末尾的一位应该是0，上一位应该加1，即变成0010。用这种加法法则，我们能够从最小的状态0000加起，一直加到1111，至此得到二进制转10进制的编码表。

我们可以将A端口不同，其余端口相同的二进制状态加以比较，发现它们都相差8；同理B端口不同，其余端口相同的二进制状态之间相差4；C端口不同，其余端口相同的二进制状态相差2；D端口不同，其余端口相同的各个状态之间相差1。

这个规律可以表示为：十进制数=A×8+B×4+C×2+D×1。其中A、B、C、D为各自端口的当前状态，0表示弹起，1表示按下。如果用上面的公式来输入0～9的数字，其中默认需要将转化的十进制数减1，得到图7所示的输出结果。

至此，我们用科学探究的方法，研究了如何用四个独立的二进制数表示0～9共10个数字，在解决这个问题的过程中，我们发现了四个独立二进制数所能表示的状态总数，并且知道了如何建立一个编码表，找到了二进制的进位法则，并且通过对这个法则的深入研究发现了二进制数转十进制数的转化规律，并且依照这个规律将程序简化。本单元的内容在整个感测与控制技术的课程体系中处于非常核心的位置，二进制的编码是从数字化的开始也是通信技术的基础。本章内容，期望通过探究的方式，而不是讲授，让学生理解为什么二进制和十进制的转化方式是这样的，这种讲法，在之前的信息技术教材中是少有的。而将科学探究的过程引入到信息技术教学中，将原本“转换公式”这种程序性知识，转化为“基于项目的学习”的过程性知识，是信息技术基础理论教学视角的一种转变，而使用科学探究的方法，让学生体验学科专家类似的研究过程，也是为了提高学生面对复杂的真实情境的问题解决能力，这种科学探究的方法，将会在后续文章中反复涉及。endprint