定积分概念的建模教学法

郭 新

（濮阳职业技术学院数学与信息工程系 河南濮阳 457000）

定积分概念的建模教学法

郭 新

（濮阳职业技术学院数学与信息工程系 河南濮阳 457000）

要教会学生如何用所学的数学知识去解决实际问题，教学过程中的数学建模思想必不可少，在概念教学中不妨使用建模教学法，把数学与实际问题的解决紧密结合起来，既培养了学生的数学修养，又培养了学生运用数学的能力。下面以定积分的概念为例，通过数学建模的方法去讲解，让学生看到概念脱胎于实际的过程，从而对数学的学习作用进一步理解，激发了学习数学和运用数学的兴趣。

启发讲授式；定积分概念；数学建模

大多数的数学概念都是由实际问题引出来的，如导数的概念，是在十六、七世纪时，欧洲科学家们在求一个物体(其运动规律已知)在某时刻的瞬时速度时引出的。导数概念的产生为微分学的建立打定了基础。同样，定积分的概念也在由一个实际问题引出的，这个实际问题就是求已知平面曲线所围成的平面图形的面积。

用基础的数学知识去解决实际数学问题是数学建模的思想，通过建模比赛可以培养学生应用数学去解决实际问题的初步思想和方法，培养其创新意识和创新能力。要教会学生如何用所学的数学知识去解决实际问题，教学过程中的数学建模思想必不可少，在概念教学中不妨使用建模教学法，把数学与实际问题的解决紧密结合起来，既培养了学生的数学修养，又培养了学生运用数学的能力。下面以定积分的概念为例，通过数学建模的方法去讲解，让学生看到概念脱胎于实际的过程，从而对数学的学习作用进一步理解，激发了学习数学和运用数学的兴趣。

一、构建实际问题引入

图5-1

二、建模过程

显然这个面积没有公式可套，因为有一条边是曲边，(如果曲边成直边，可用梯形公式)在数学中，我们知道，新的概念建立在已知概念的基础上，也就是说，这个未知的曲边梯形的面积将要和已知的直边梯形的面积建立联系，即要把曲边形转化(回归)成直边形，从而可用公式。但如何进行这种转化呢？结合一下导数概念中求瞬时速度时的处理方法。不难想到下述方法。

(一)分割

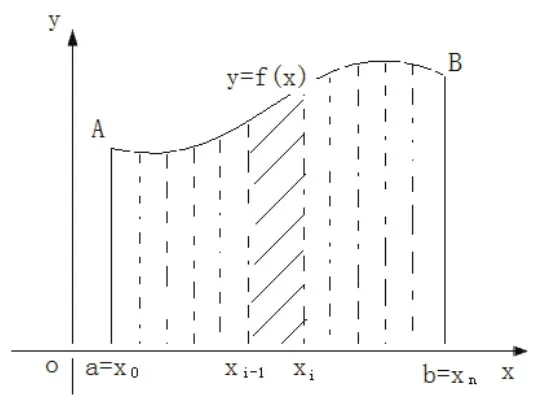
图5-2

2.过每一个分点作平行于y轴的直线，这样一来，大的曲边梯形AabB被分成n个小曲边梯形

(二)近似代替：

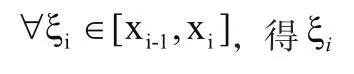
(三)求和：

把n个小曲边梯形加起来，就得到大曲边梯形面积的近似值。

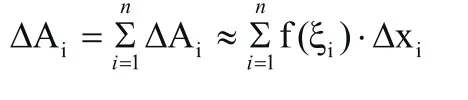
(四)取极限 (极限是近似向精确转化的桥梁)

三、实际问题的解决

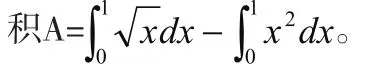
[1]常瑞玲.高等数学[М].北京工业大学出版社,2010,9.

The modeling method of the concept of definite integral

Guo Xin

(Department of Mathematics and Information Engineering,Puyang Vocational and Technical College, Puyang Henan, 457000, China)

To teach students how to use mathematical knowledge to solve practical problems, the essential mathematical modeling thought in the teaching process, may wish to use the modeling teaching method in the teaching concept, to solve the mathematics and practical problems are closely combined, can not only cultivate students mathematics training, and cultivate the students' ability to apply mathematics. The following concept to the definite integral as an example, through the mathematical modeling method to explain, let students see the concept originated in the actual process, so as to further understand the role of mathematics learning, stimulate their interest in mathematics and applied mathematics.

Heuristic teaching style;the concept of definite integral ;mathematical modeling

O172.2

A

1000-9795（2014）03-0224-01

［责任编辑：刘丽杰］

2014-01-12

郭 新（1977-），女，河南濮阳县人，讲师，从事概率论与高等数学教学研究。