小波变换在AT 供电牵引网故障测距中的仿真研究
2014-03-17王喜燕陈乐瑞
王喜燕,陈乐瑞
(郑州铁路职业技术学院,河南 郑州 450052)
0 引言
接触网故障的精确定位对缩短高速电气化铁道抢修时间,提高运输效率具有直接的影响。由于在输电线路方面,对故障定位的研究已经十分成熟,因此,本文对接触网中的AT 供电方式进行了故障测距的仿真分析。
1 接触网行波法原理
由图1 所示的故障行波过程可以得到能用于故障测距的两个基本关系。

图1 A 型行波测距原理图
当故障点位于测距点到线路中点Z 的区间时,m端在测距点收到的第二个到达m 端的反射行波浪涌是故障的反射波ρFρmuF,则由m 端测出的距离为:
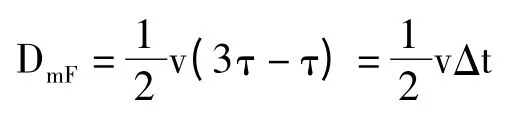
DmF表示测距端m 到故障点F 之间的距离。
当故障点位于测距点到中点Z 以外的区域时,第二个到达n 端的反向行波浪涌是对侧母线的反射波通过故障点后的折射波γFρmuF,它先于故障点的反射波ρnuF到达n 端,于是n 端测出的距离是:
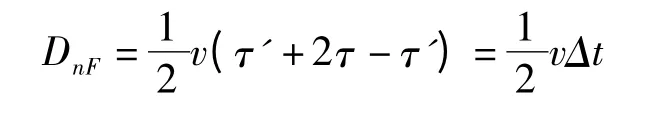
DnF表示对端m 到故障点F 之间的距离。
显然,当故障点F 与线路中点重合时,对线路任一端而言,都有故障点反射波与对端母线反射波同时到达的情况出现。这时,两端都能测出本段到故障点的距离。由此而见,可靠准确的识别第二个反向行波浪涌对正确实现故障测距是十分重要的。其中一种方法就是小波变换法。
小波变换法是根据行波信号在其小流变换下的模极大值实现故障测距的一种算法。它的理论依据是有故障点产生的或由线路开关合闸产生的初始行波,来自故障点的反射波,检测母线相邻母线的反射波,对端母线的反射波、中间换位点、噪声信号等在不同尺度下的小波变换都将呈现模极大值,根据不同尺度下的小波变换模极大值及其变化,并与接于同一母线的健全线路行波波形相比较,可以有效地识别出来自故障点初始行波和反射波,以实现故障测距。
2 小波理论
准确、充分地提取故障信息是研究各种保护原理的关键。故障时系统的频率成分随时间的变化而变化,然而暂态信号是随机的、非平稳的,只能在纯频域分析的Fourier 变换就显得无能为力了。小波变换在时频域都具有良好的局部化性能,能更准确地描述暂态信号的故障特征,是分析暂态信号的有力工具,同时高速采集技术对小波变换技术应用于暂态量保护提供了保障。
2.1 连续小波变换
若ψ(t)∈L2(R)满足容许条件∫ψ(t)dt=0,则称ψ(t)为小波基,对小波基做伸缩和平移得:

称ψs,b(t)为小波函数,其中s 为与频率对应的尺度参数,b 为与时间对应的位移参数。对于L2(R)的信号f(t),其连续小波变换可定义为:

一维信号f(t)经连续小波变换生成的Wf(s,b)所包含的信息有冗余的。在实际应用中计算机处理的数据都是离散的,所以要想不丢失信息,必须在离散的尺度参数s 和位移参数b 下进行小波变换,从而得到离散小波变换。
2.2 离散小波变换

对应的小波变换为:

为了使小波变换在时间和频率都具有灵活的分辨率,适应暂态信号的非平稳特性,就需要改变s,b的大小。最常用的是取a0=2,b0=1,则a=2j,b 仍然保持连续变化,从而得到二进小波:
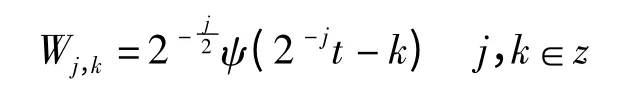
离散小波实际是小波积分变换的窗口函数。窗口函数的时间窗随着尺度函数s 的减小而自动变窄。当中心频率过高时,它具有较宽的频窗;当中心频率较低时,它自动扩大时窗。由此可见,离散小波具有极其敏感的变焦特性,很适合对暂态信号的分析。
2.3 暂态保护中小波基的选择原则
在对电力系统暂态信号进行小波变换时,选取合适的小波基对于故障特征的准确提取具有重要意义。
小波变换在时域中表示为信号和小波基的卷积形式。如果小波基的波形与被分析信号的波形相近,则相近部分的特征将被放大,不同部分的特征将被抑制,从而提取故障暂态特征。由于暂态信号具有冲击性,而db 系列小波与冲击性信号的波形相似系数相对于Haar、Meyer 小波要大得多,因此db 系列小波最能提取暂态信号的股中行特征。小波基的性质相互制约,不可能同时达到最佳,经过反复比较,本文选用具有正交、紧支以及高阶消失矩的db4 小波进行多尺度小波分析。
3 接触网行波测距的仿真研究
AT 供电方式下接触网ATP 仿真模型如图2。16km 处故障过渡电阻为1 欧时电流波形及小波变换如图3。6km 处故障过渡电阻为100Ω 电压相角为45°时电流波形及小波变换如图4。故障距离分别为6km、16km、26km、36km、46km,过渡电阻分别为1Ω、10Ω、50Ω、100Ω 时的仿真数据如表1 所示。故障距离分别为6km、16km、26km、36km、46km,过渡电阻为100Ω,故障电压相角为45°、135°、225°、315°时的仿真数据如表2 所示。

图2 AT 供电方式下接触网ATP 仿真模型
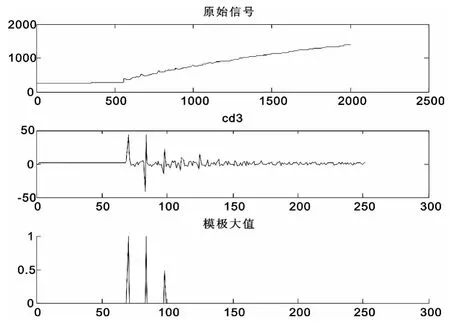
图3 16km 处过渡电阻为1Ω 时测量点电流波形及小波变换
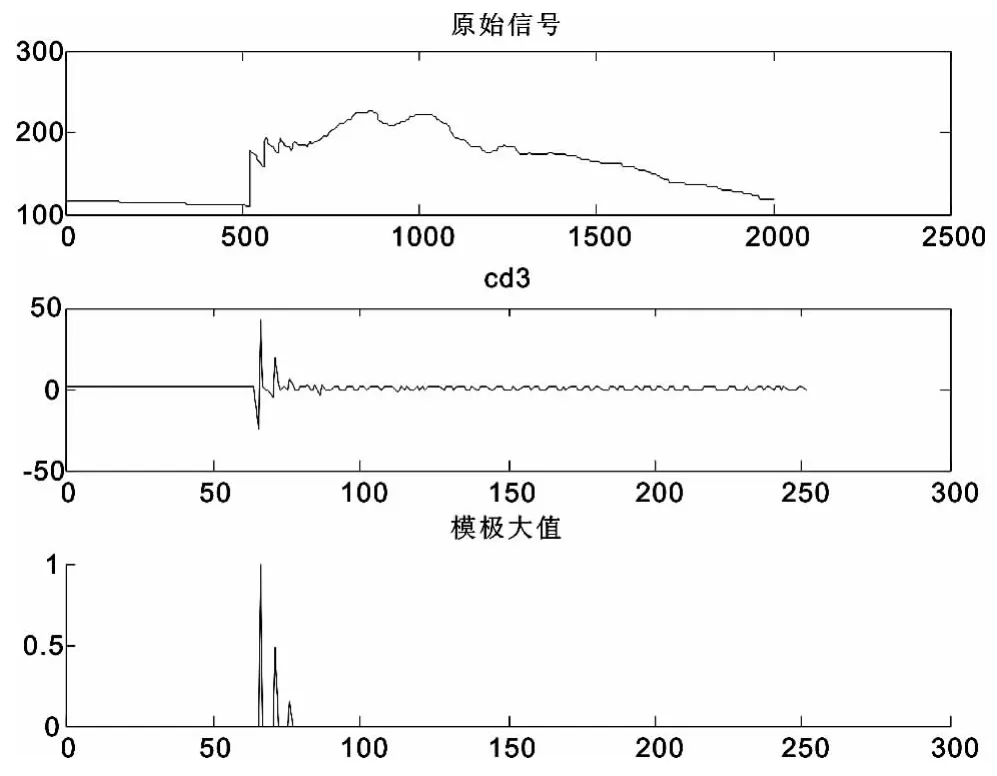
图4 6km 处故障过渡电阻为100Ω 电压相角为45°时电流波形及小波变换
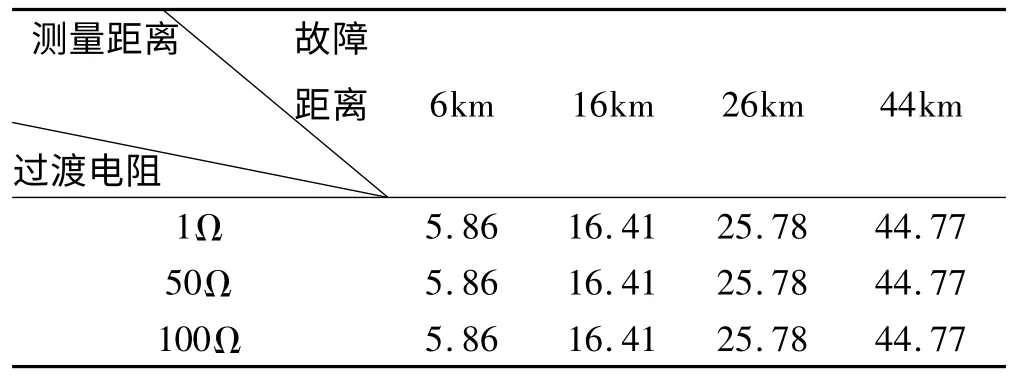
表1 不同过渡电阻下仿真数据
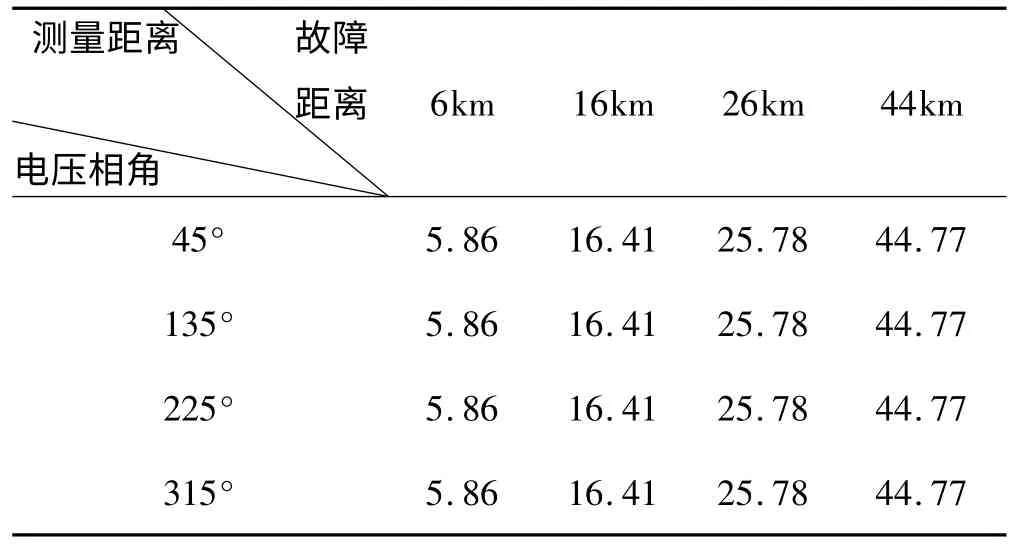
表2 不同过渡电阻下仿真数据
4 结论
通过以上的仿真数据得知过渡电阻和故障时刻的电压相角对行波测距基本没有什么影响。对仿真模型的影响因素涉及到的其他问题,如牵引网行波波速的确定,并联补偿电容组,牵引网上下行线路之间的电磁耦合,线路上是否有保护线等,如何提高故障检测精度,还有待日后深入地研究。
[1]葛耀中.新型继电保护和故障测距的原理与技术[M].西安:西安交通大学出版社,2007.
[2]张德丰.MATLAB 小波分析[M].机械工业出版社,2009.
[3]杨毅波.超高压输电线路单端暂态量保护元件的研究[D].南昌:华东交通大学,2010.
[4]于万聚.高速电气化铁路接触网[M].成都:西南交通大学出版社,2003.
[5]曹笃峰.电气化铁道接触网行波故障测距研究[D].北京:北京交通大学,2007.
[6]李伟,王倩,刘超.行波法应用于复线牵引网故障测距的仿真研究[J].铁道运输与经济,2008,06(6):89-95.
