重心法下考虑运输时间的配送中心选址决策

阮国祥，尹宇起，傅克俊

(山东工商学院管理学院，山东 烟台264005)

物流活动的最终目的是用最低的成本、最短的时间为客户提供最好的服务以满足客户的需求。物流配送中心作为支干线运输的中转中心，起着承上启下的作用。因此，配送中心的合理选址有利于降低物流成本，同时可以减少运输过程所用时间从而提高整体服务效率。关于单一物流配送中心的区域选址问题研究已有较多的文献，一般认为重心法是解决此类问题较为合适的选址方法，并在实际决策中应用较广泛［1］。但是，重心法在实际应用也中存在一定的缺陷，例如重心法是根据总运输成本最小进行选址决策的，但如此以来运输时间因素在决策中被忽略了。而在很多情况下，时间成为市场竞争的关键要素，为客户高度重视。因此，从运输时间的角度对现有重心法进行改进，以权衡配送成本与时间，使物流配送系统的整体效益最优。

一、理论模型

1．重心法模型

重心法是一种用来寻求最优配送中心的常用数学模型。其优点是按运输费用最小的原则来选址，并对候选位置不加限制，因此具有较大的灵活性。从重心法的改进和发展过程的可知，成本因素一直是学者们研究的重点［2-3］。可是对于最优成本的一味追求并不完全符合现代物流经营理念的要求。在时间资源对于客户重要性不断提升的社会背景下，时间要素同样应该纳入决策范畴之内。

假设在一直角坐标系中，需新建配送中心的坐标为P(ai，bi)，n个配送需求点 Wj的坐标为(xj，yj?，欲求此配送中心的位置，需满足从配送中心到各配送点的总运输费用最小，其坐标点需要通过多次迭代计算获得。重心坐标(a，b)计算如公式(1)所示，运输费用T计算如公式(2)所示。wj为新建配送中心P与需求点Wj之间的物流量;rj为配送中心到各需求点Wj的每单位物流量单位距离所需的运输费用(运输费率);dj为配送中心到各需求点Wj的直线运输距离。

2．聚类分析

聚类分析是根据事务本身的特征研究个体分类的基本方法，其基本原则就是同一类中的个体有较大的相似性，而不同类的相似性较差［4］。本文运用的聚类分析法是系统聚类中的最短距离法，其基本步骤和原理表述如下:(1)以绝对值距离作为两样本点间的距离，以最短距离作为两类间的距离;(2)计算N个样本点两两之间的距离，得到距离矩阵;(3)构造个类，一个样本点作为一类;(4)合并类类之间距离最小的两个类为一个新类;(5)计算新类与其他各类的距离。若类的数目为1，则转到步骤(6)，否则回到步骤(4);(6)画出聚类图;(7)决定类的个数和类［5］。

通过聚类分析将配送点分成几个类，简化后续模型求解的复杂性，此模型可以满足大量配送点求解问题。聚类分析后的相关要求:将类内包含需求点的运输量之和作为类的运输量;以类内各点与配送中心点直线距离最小的点作为类的代表点。

3．运输时间的确定及最优性选择

由于选址点是一个区域，具有连续性、无穷性和计算的复杂性，因此很难确定运输时间。所以借鉴物流位图法的思想对模型进行简化求解［6］，本文将这种方法定义为等距位图法，其具体步骤如下:(1)以类内各点的运量总和作为类的运输量，求出各类的运输量占配送中心运量的权重P(k)，而后按权重P(k)大小进行排序;(2)将确定好的代表点Bk作为圆心;(3)画出各代表点Bk的等运距线束(由于是简化模型，等距线表现为同心圆，且半径可根据实际调整);(4)找出不同代表点在某一事先确定区域的等运距曲线束的交点;(5)求出各交点At的总运距Lt=∑kL(k)P(k);(6)比较各交点At的总运距，选择其中总运距最小的点L*

t作为配送中心点。当总运输距离减小时，可以使配送中心用更短的时间满足客户的需求。而且备选的选址点分布在在一个总运费受到限制的范围内，因此既可以减少运输时间，又可以控制配送成本，同时用等距位图法还简化了非线性规划问题。

二、算例

已知某工厂坐标位置C及各配送点Wj的坐标位置，现需要新建配送中心P，将工厂生产的产品配送到各处，问此配送中心应建在何处最为经济合理。已知各设施的坐标位置和产品需要量，如表1。

表1 配送点和工厂的坐标分布与送货量

如果从工厂到配送中心的运费率为r8=20;从配送中心到各个配送点的运费率为r1=r2=…=r7=50，利用上述思路对该问题进行求解，主要步骤如下:

1．重心法对配送中心的精确求解

再将初始值(a0，b0)代入式(1)中，求出配送中心的改进位置(a1，b1);再利用式(2)计算出与(a1，b1)相应的总运输费用T1;将T1与T0进行比较，若 T1＜ T0，则返回步骤(2)，若 T2≥T1，说明(a1，b1)便是最优解。如此反复迭代计算，直至T(k+1)≥T(k)，求出(ak，bk)这一最优解为止。

由此计算出最小运费配送中心坐标为(8．39，7．86)，此时的总运输费用为39 520元。

2．配送点的聚类分析

本文采用最短距离法进行聚类分析，最短距离法的计算方法如下:

用记号Smn表示样品 Wm与Wn之间的距离S(Wm，Wn)，用Gp和Gq分别表示两个类，用记号D(Gp，Gq)和Dpq表示类Gp和类Gq之间的距离，记号Gr={Gp，Gq}表示类Gp和类Gq合成的新类。类Gp与类Gq中最近的两个样品之间的距离定义为这两个类的距离即最短距离，具体公式为:

当类Gp和类Gq合并成新类Gr后，仍然按照最短距离法计算新类Gr与其他类Gl(l≠p，q)之间的距离，具体公式为:

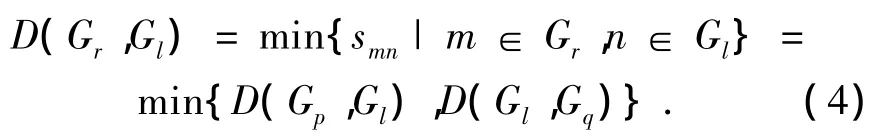
由于工厂的位置比较远，因此先不考虑工厂，在最后决定类的个数时再将其考虑在内。配送点两两之间的距离见表2。

表2 各配送点间距离

用聚类分析法分区过程如下:

先把各个配送点单独视为一类，则由已知案例可知现有7类{G1}{G2}{G3}{G4}{G5}{G6}{G7}(工厂也单独成类G8)。再在表2中找出最短距离最小值为s13=4．22，则将第1类与第3类合并成一类 G9={G1，G3}，然后按照公式(3)、(4)重新计算类间距离。然后按照上述步骤计算，最终所有对象都被合并成一类，根据计算过程做出聚类图，如图1。

由于工厂到配送中心的距离远且运量大，适合干线运输。若在此考虑的话，会产生配送中心较大偏离。所以仅将需求点分为三类{G1，G2，G3}，{G4}，{G5，G6，G7}。

最后确定各类的代表点及运量。各配送点到配送中心的距离和运量如表3。

表3 配送中心到各配送点的距离与运量表

3．运输时间优化的配送中心点选择

根据聚类分析计算，设代表点B1表示 {G1，G2，G3}，B2表示{G4}，B3表示{G5，G6，G7}。代表点运量为 wB1=30，wB2=5，wB3=45，按照运量求出代表点的权重，具体如表4。

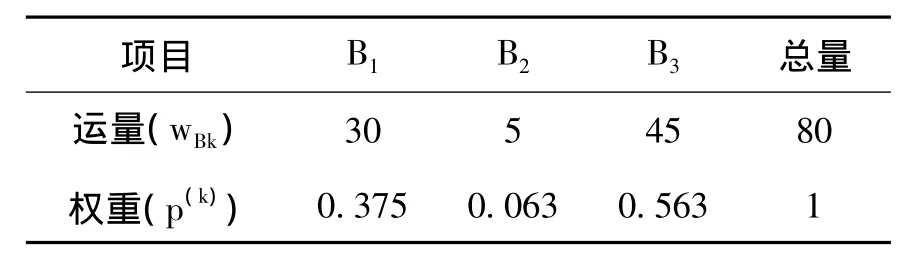
表4 代表点运量权重表

由于p(3)＞p(1)＞p(2)将代表点的优先级顺序确定为 B3，B1，B2。

图1 配送点聚类图

配送中心成本限制区域是以重心法下求得的原配送中心选址点((8．39，7．86)为圆心，半径为1的圆域(考虑模型的简化，以圆代替封闭等值曲线围成的凸集)。

确定各代表点等距线L，L分别定为2、3、4做圆，如图2。

其中 A1(8．54，7．28)，A2(9．01，7．50)，A3(8．99，8．28)，A4(8．70，8．50)，A5(7．79，7．05)为得到的若干交点。

图2 等距位图

计算At各点对应的总运距Lt=∑kL(k)P(k)，计算结果如表5。

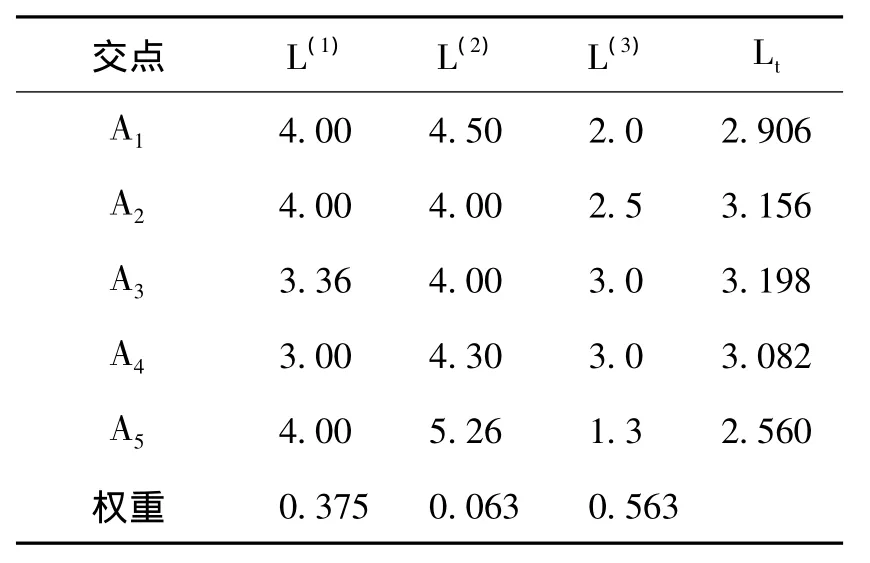
表5 总运距计算表

由表中 Lt列可知 L*5对应的 A5(7．79，7．05)为最合适的配送中心选址点。

各配送点和工厂到该配送中心总运费可通过表6获得。

若以原配送中心选址点(8．39，7．86)计算，总运距Lt=2．863＞2．56。其运费和运距结果比较如下:

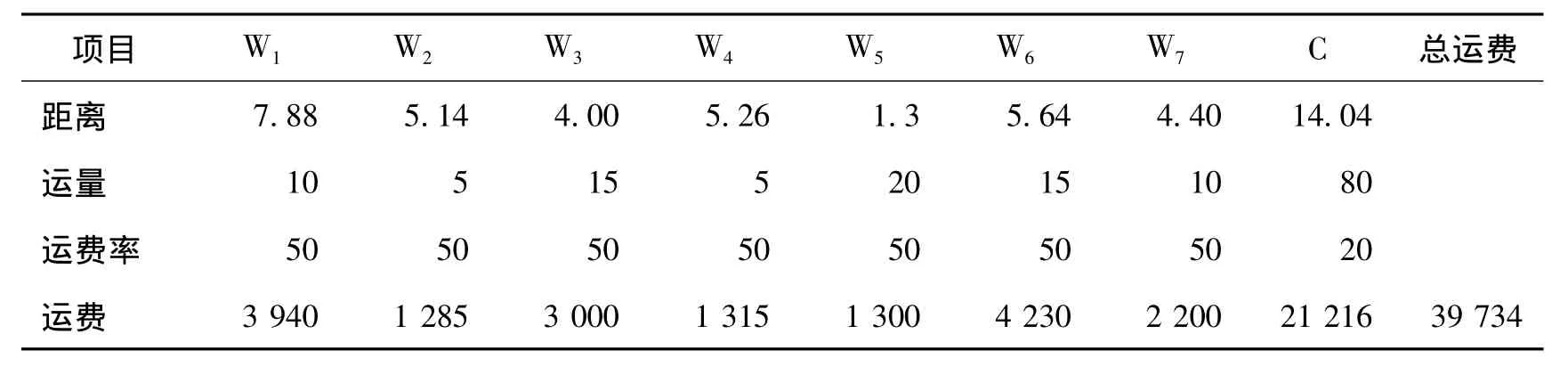
表6 总运费计算表

通过比较可以看出，选择在 A5(7．79，7．05)建配送中心，其总运输距离相对于原方法求得的选址点减少了10．58%，在运输速度不变的情况下，意味着运输时间缩短了10．58%，且费用仅增加0．54%，并未出现较大幅度的增长，说明 A5(7．79，7．05)为适合配送中心的选址点。

三、结论

重心法的优点是仅以运费最小为原则，对于候选位置不做其他的限制，因此这种方法应用范围较广。但由于这种灵活性，可能计算出在现实不可能选择的位置，这是重心法的缺点。配送时间目前已成为影响客户服务水平的关键因素，减少配送运输时间可以大幅度提高客户满意度［7］。本文将配送中心的筛选由点扩到某个成本限制区域，而且考虑运输时间，这样模型更符合实际的要求，具体方法为通过聚类分析和等距位图法的结合确定具有可行性的配送中心点，并计算各点对应的总运输距离，从中选择运距最小者，相应也为运输时间最短者。本文提供了一种应用重心法进行配送中心选址的新思路，在牺牲一定的运输成本前提下，使运输速度能得到明显改善，满足了客户对时间的要求。

［1］邹辉霞，高伟．单配送中心的离散选址模型［J］．科技进步与对策，2004，21(1):77-78．

［2］鲁晓春，詹荷生．关于配送中心重心法选址的研究［J］．北方交通大学报，2000，24(6):108-110．

［3］王家聚．基于重心法的配送中心选址研究及应用［J］．长江大学学报:社会科学版，2008，31(4):64-66．

［4］赵芹．基于聚类分析和重心法的第三方物流企业配送中心选址分析［J］．物流技术，2011，30(8):101-114．

［5］陈东升，李科学．Fuzzy最大树聚类方法及其应用［J］．运筹与管理，2008，16(3):69-73．

［6］王槐林，刘明菲．物流管理学［M］．武汉:武汉大学出版社，2010．

［7］林珊，段复建．一个物流配送中心选址模型及其算法［J］．吉林大学学报:自然科学版，2012，33(6):29-32．