共形球面阵天线的三维方向图综合算法*

姜 兴,张 凯,蓝雪梅

(桂林电子科技大学 信息与通信学院，广西 桂林541004)

近年来，将智能优化算法比如遗传算法、粒子群算法等用于解决阵列方向图综合问题，已经司空见惯。从最近几年关于各种算法的改进和讨论来看，主要包括对算法具体参数变量的调整[1-3]、混合各种算法的优势[4-7]这两方面的改进。

主要目的都是为了弥补各种算法的不足，发挥各种算法的优势，实现扬长避短的初衷。然而稍显不足的是，这些算法目前主要集中在解决阵列的二方向图波束赋形，例如笔形波束、平顶波束、余割波束等。实际上，共形阵方向图综合是一个三维优化问题，仅仅用二剖面赋形结果代替实质上的三维优化，难免与最终的实际情况有所差异。尤其是共形球面阵的波束成形问题，用二优化算法显然有些无能为力，比如空间波束指向就是一个三维问题。因此，本文研究了一种共形球面阵天线的三维方向图综合算法。

1 三维方向图综合算法

本算法由3个子算法组成：核心算法、阴影算法、波束成形算法。

算法具体流程如下：

(1)预处理阶段。首先完成球面阵的建模，在实际阵列前提下，通过电磁仿真软件提取各阵元的远场数据，或者得到实测数据。这种情况下的数据，考虑到了互耦以及载体的影响；

(2)核心算法阶段。调入第一步得到的每个阵元的远场数据，并进行处理。进入下一步；

(3)阴影算法阶段。根据期望主波束指向，计算阴影区域的具体阵元。进入下一步；

(4)波束成形阶段。结合前两步，得到实际工作阵元的远场数据，进行方向图加权处理；

(5)迭代阶段。重复(2)～(4)步骤的过程，达到目标值或者迭代次数后算法终止。

1.1 核心算法

目前主流进化算法有遗传算法(GA),粒子群算法(PSO)等。GA虽具有全局搜索优势，但收敛慢，原因在于GA存在编解码过程，即便采用实数编码的方式，仍然需要解码。而PSO不需要编解码的过程，直接对变量优化，并且PSO原理简单，实现容易，参数少且收敛快。因此，核心算法采用PSO为主体，可以避免GA初期的编码过程。然而，PSO容易陷入局部最优，因此在PSO基础上，引入GA的交叉变异机制，一旦算法判定粒子陷入局部最优，则进行交叉变异，使其迅速摆脱束缚；变异之后，再进行二次插值，使粒子进一步突破，飞向全局最优解。

为了进一步提高收敛速度，本算法提出了自适应加速因子。标准PSO的速度和位置更新公式如下：

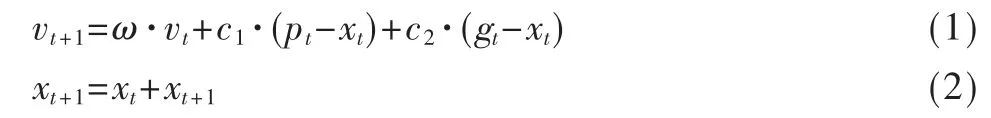
其中，t是进化代数，ω是惯性权值，c1、c2是加速因子，c1表示粒子的自我认知，c2表示粒子的社会认知，xt、vt分别是粒子在当前迭代时的位置和速度，pt、gt分别是粒子的个体最优位置和全局最优位置。标准算法中，c1、c2为定值，典型值为c1=c2=2。

在算法前期加速因子取的较大，使得粒子飞得更快，快速找到局部最优，到了算法中后期为避免陷入局部最优，加速因子则慢慢变小。同时，一旦算法判定当前最优值长时间没有更新，则进行变异，跳出局部最优。从而找到全局最优解。因此，把标准粒子群算法的定值加速因子改成如下动态因子，实现自适应加速。

其中，tmax为最大迭代次数。并且c1、c2的公式相同，这表示粒子的自我认知部分和社会认知部分对粒子速度的权重影响相同，同等重要。

目前报道的大多数关于共形球面阵的文献，均假设单元为理想点源，并为简化，忽略了阵元之间互耦的影响[8-10]。然而这与实际情况不符，因此优化得到的方向图与理论结果有很大差异。所以需要采用实际的阵元来进行优化，还要考虑互耦。故在预处理阶段，提取了各阵元的远场仿真数据，采用方向图叠加原理来处理共形阵的优化问题，自然也考虑了互耦的影响[11]。

1.2 阴影算法

以图1所示的共形圆环阵为例来说明阴影问题，圆环上均匀分布10个阵元，各阵元最大波束指向均为圆环径向，假设期望共形阵主波束指向角度为(θ,φ)，要求波束宽度为α；对于阵元来说，由于它们最大波束指向各不相同，在偏离阵元最大波束指向后，各阵元在远区辐射场逐渐减小，因此，在阵列主波束覆盖范围α内，某些阵元实际上并没有贡献，反而在主波束以外区域增大了副瓣。换言之，对于阵列主波束来说，存在一个阴影区，在这个区域内的阵元没有起到有效作用，则让其停止工作，不参与阵列主波束成形。因此，阴影算法的作用就是确定不工作的阵元。算法关键步骤如下：

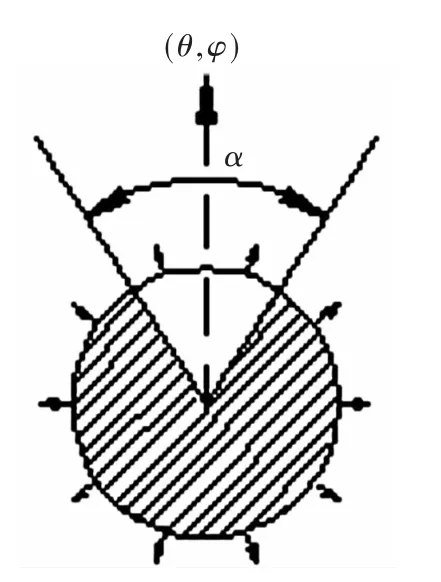
图1 共形圆环阵

1.3 波束成形算法

将工作阵元的方向图数据分别进行加权，再把所有加权后的阵元方向图进行叠加，即可得到阵列总场方向图，然后评价目标函数。

目标函数的选择至关重要，特别是对于三维方向图优化而言，约束参数较多。本算法从两个方面来构造目标函数，一个是主波束区域，另一个就是干扰区域。在主波束区域里，需要关注的是主波束3 dB波束宽度，包括θ 和 φ 两个方向波束宽度；而主波束指向为(θ,φ)，确定了指向和波束宽度之后，就可以确定主波束区域的成形要求。

干扰区域包括两部分，一个是在主波束以外区域的旁瓣，另一个就是主波束区域的交叉极化分量。为此，把远场方向图数据矩阵作进一步处理，分成主极化分量矩阵和交叉极化分量矩阵(交叉极化采用Ludwig第三定义计算)。每次迭代中，分别对这两个矩阵加权，然后根据方向图叠加原理得到加权后的主极化方向图矩阵Comatrix和交叉极化方向图矩阵Cross-matrix。主波束区域的数据位于Co-matrix中；干扰区域的数据由两部分组成，一部分是Co-matrix中主波束区域以外的数据，另一部分是Cross-matrix中的所有数据。

然后构造目标函数。假设目标方向图为Ed，实际加权方向图为Eo，F表示目标方向图Ed的波动大小。因此主波束区域的目标函数可以表示为：

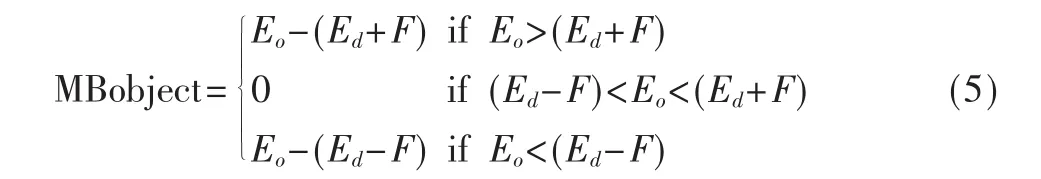
主波束适应性函数取为目标函数的均方差，c为主波束区域点数：

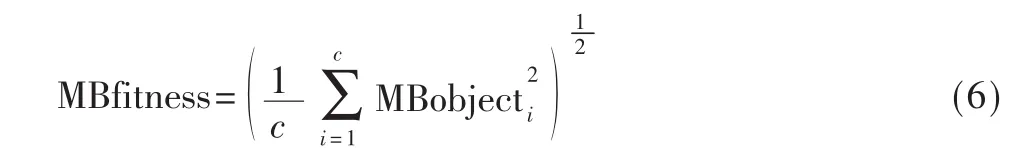
干扰区域则相对简单,只要给定一个上限值SL即可。因此干扰区域的目标函数表示为：

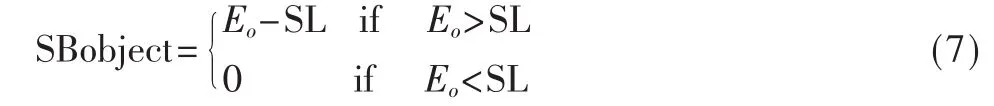
干扰区适应性函数也取为目标函数的均方差，h为干扰区点数：

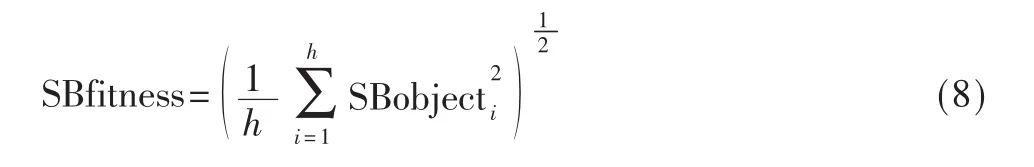
因此总适应性函数为：

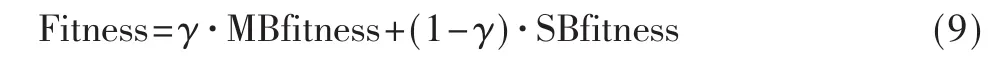
其中γ为权值比重。

2 共形球面阵三维方向图波束形成

共形球面阵模型如图2所示。半球面上均匀分布了4层共37个圆极化天线单元，每层单元按逆时针编号。假定指标要求如下：主波束指向(θ,φ)为(15°,180°)，θ方向 3 dB波束宽度为 20°，φ方向为 40°,旁瓣小于-15 dB。优化后的主波束方向图如图3所示，其中图3(a)为俯仰面方向图，图3(b)为方位面方向图；三维远场方向图如图 4所示，图 4(a)为主极化远场方向图，图 4(b)为交叉极化远场方向图。表1为优化后各阵元的幅相权值。

本文研究了一种共形球面阵天线的三维方向图综合算法，详细说明了该算法原理及关键步骤，并将其运用到共形球面阵的波束成形设计中，取得了良好效果。该算法主要特点是:(1)在核心子算法方面，以粒子群算法为基础，吸收了主流优化算法的优势，并采用自适应因子和二次插值算子改进性能；(2)提出了阴影算法，用于解决共形阵的单元选取问题；(3)在波束成形方面，分别构造主波束区域和干扰区域的目标函数，并且主极化和交叉极化方向图分开优化，更有利于研究和分析主极化分量和交叉极化分量对总场方向图的影响。仿真计算结果表明，该算法可以解决共形球面阵天线的方向图综合问题。

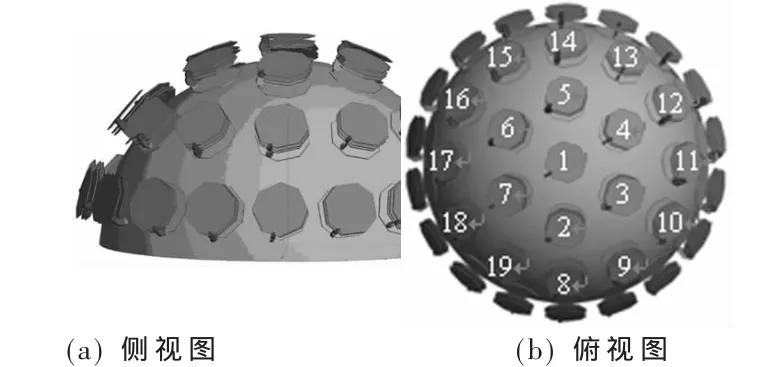
图2 共形球面阵模型

图 3主波束指向在(15°,180°)时优化后的方向图

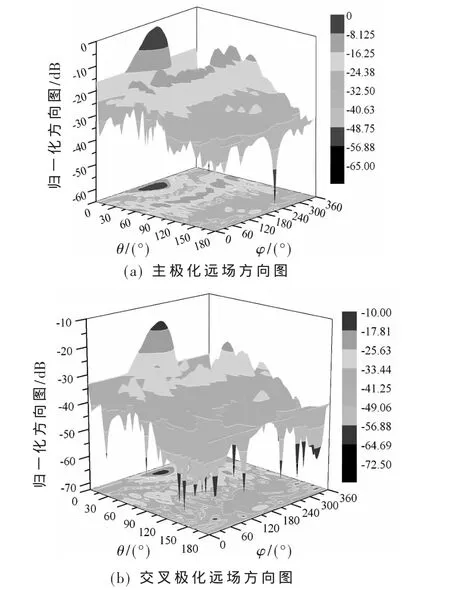
图 4主波束指向在(15°,180°)时优化后的三维远场方向图

表1 优化后的阵元幅相权值

[1]NIKNAM T,GOLESTANE F,BAHMANIFIROUZI B.Modified adaptive PSO algorithm to solve dynamic economic dispatch[C].Power Engineering and Automation Conference(PEAM),IEEE,2011,1(1):108-111.

[2]MODIRI A,KIASALEH K,Efficient design of microstrip antennas for SDR applications using modified PSO algorithm[J].IEEE Transactions on Magnetics,2011,47(5):1278-1281.

[3]KRISHNAMOORTHY H S,VADALI M K,SUPEDA P.A novel,empirical equation-based shunt active filter for harmonic elimination and power factor correction,using a modified PSO algorithm[C].India Conference(INDICON),Annual IEEE,2011,1(5):16-18.

[4]胡瑞,丁香乾,张峰,等.基于混合遗传算法的多约束集装箱装载问题研究[J].电子技术应用,2006，32(2):24-26.

[5]Wu Junqiang,AIJIA O,Liu Libin.A self-adaptive hybrid algorithm of PSO and BFGS method[C].International Conference on Industrial Control and Electronics Engineering(ICICEE),2012,1690:23-25.

[6]GRIMACCIA F,MUSSETTA M,ZICH R E.Genetical swarm optimization:Self-adaptive hybrid evolutionary algorithm for electromagnetics[J].IEEE Trans on Antennas Propag,2007,55(3):781-785.

[7]BABAEE H,KHOSRAVI A.An improve PSO based hybrid Algorithms[C].2011 International Conference on Management and Service Science(MASS),2011,1(5):12-14.

[8]Huang Zhiyong,BALANIS C A.Adaptive beamforming using spherical array[C].Antennas and Propagation Society International Symposium,2005 IEEE,2005,4A:126-129.

[9]杨继波,陈客松,胡进峰,等.共形球面阵建模及其旁瓣控制的研究[J].电子技术应用,2010,36(11):154-157.

[10]MANDRIC V，RUPCIC S，ZAGAR D.Optimization of the spherical antenna arrays[J].ELMAR,Proceedings,2012,287(292):12-14.

[11]欧阳骏.共形天线及阵列的分析和综合研究[D].成都：电子科技大学，2008：131-140.