基于MATLAB的探空火箭测控系统仿真
2014-03-16康海龙姜秀杰
康海龙 , 姜秀杰
(1.中国科学院空间科学与应用研究中心 北京 100190;2.中国科学院大学 北京 100049)
探空火箭是一种在近地空间进行探测和科学试验的火箭,其飞行高度介于探空气球与卫星之间,是临近空间40~300 km唯一的、其他飞行器所不能及的实地探测火箭[1]。不同于人造卫星等其他航天器,探空火箭大多数近似于垂直地面发射,飞行距离短,飞行高度变化快,适合中高层大气电离层立体剖面探测;探测载荷在轨时间短,火箭与地面站需在短时间内保持通信链路的畅通;火箭姿态变换迅速,尤其再入大气层时气流冲击强,姿态难以保持稳定。因此,探空火箭地空通信问题具有一定的特殊性[2]。
在任务中,测控系统担负着监测任务过程,获取任务数据的重要任务。利用仿真方法对总体方案设计、测控精度分析等关键环节进行研究,对于验证和优化总体设计方案,提高试验任务效果和试验任务成功率是十分必要的[3]。
1 仿真方案设计
探空火箭点火起飞后即按照预定的弹道和姿态飞行,由于地面测控设备的测控性能与探空火箭的弹道和姿态有密切的关系,因此,分析探空火箭测控性能的前提条件就是对探空火箭的弹道和姿态进行仿真。探空火箭测控性能分析中需要计算地面站对探空火箭的跟踪距离和仰角以及天线安装角等[4]。对探空火箭测控系统仿真主要包括两个方面:
1)地面站对探空火箭的跟踪性能,包括跟踪距离和跟踪角度等;
2)箭载测控设备天线方向图对地面站的覆盖情况,包括天线安装角α和β的变化范围。
以探空火箭试验获得的原始数据,其中包括GPS弹道数据和姿态仪数据为基础,仿真分析利用MATLAB软件建立地面站和火箭模型算法,以时间为主线,以地面站对火箭跟踪性能和天线安装角的变化范围报告为输出,完成仿真方案的构建。测控系统仿真方案由数据输入、数据处理、数据输出显示3部分组成,如图1所示。

图1 仿真分析方案结构简图Fig.1 Structure diagram of simulation system
2 地面站对火箭跟踪模型
2.1 模型介绍
在发射前需论证天线是否满足跟踪弹道要求,判断是否会出现过顶现象,因此需要计算地面站天线的姿态角包括方位角和俯仰角,建立以P点为原点,以天文东方向为X轴方向,以天文北为Y轴方向,以天为Z轴方向的东北天导航坐标系,水平方向角度为方位角α,以正北为参考基准,取北偏东为正,角度范围为0°~360°;垂直方向角度为俯仰角β,取向上为正,角度范围为 0°~90°,如图 2所示。

图2 地面站天线姿态角Fig.2 Ground station antenna attitude angle
2.2 模型求解
跟踪计算基于已知的火箭理论弹道数据。模型算法采用GPS数据,数据内容包括火箭实时的纬度、经度和高程,由此得到火箭的位置。已知由GPS测得的地面站坐标 (纬度B0、经度 L0、高度 H0)和弹道坐标(纬度 Bi、经度 Li、高度 Hi)。
根据式(1)得到在以地面站为原点的北东天坐标系中每个弹道点 A 的位置(xi,yi,zi)。
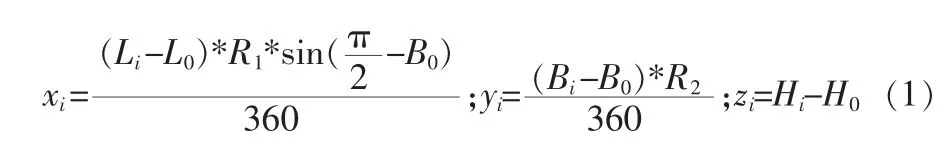
其中,赤道圈长度 R1:40075360 m;经纬圈长度 R2:39940670m。
由图2,根据式(1)的结果代入式(2),即可计算出俯仰角和方位角。

3 箭载测控设备天线安装角模型
3.1 模型介绍
探空火箭的测控性能设计中要求箭载测控设备的天线方向性图满足测控设备在时间域和空间域的覆盖要求。箭载天线方向性图可用箭体坐标系内的增益分布G(α,β)描述,定义如图3所示。为了确定箭载测控设备天线的安装角,需要计算箭体坐标系内火箭上观察、地面站视线方向形成的天线安装角α和β的变化范围。α定义为火箭横截面内的指向角III舵面为0°,迎着火箭头部看,逆时针转为增加方向,范围 0°~360°;β 定义为火箭纵剖面内的指向角, 头部为 0°,向尾部展开为正,范围 0°~180°。
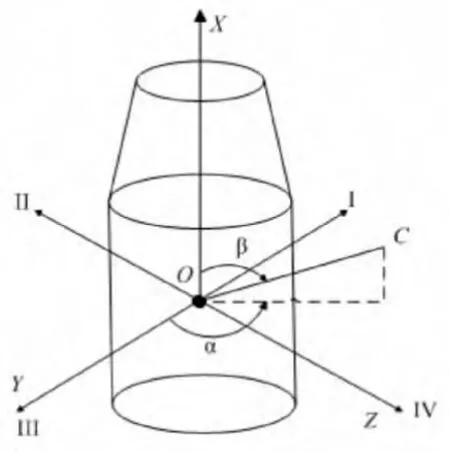
图3 箭载测控设备的天线安装角α和β的定义Fig.3 Rocket-borne antenna device antenna installation angelαandβ
3.2 模型求解
箭体坐标系固定在火箭上,随火箭一起运动。火箭变换姿态后,其箭体坐标系与地理坐标系(导航坐标系)之间的变换关系可以通过姿态旋转矩阵描述。工程应用中,对于火箭定义俯仰角为火箭纵轴(+X轴)在发射坐标系XOY平面上的投影与发射坐标系+X轴的夹角,航向角为火箭纵轴 与发射坐标系XOY平面的夹角,滚转角为火箭纵轴的铅垂面与纵对称的夹角。火箭姿态用3个欧拉角表示,分别为航向角ci、俯仰角bi、滚转角 ai[5-6]。姿态由这3个欧拉角的旋转顺序和旋转角度决定。根据矩阵运算的性质可知,矩阵相乘的顺序不同,结果也不同。姿态测量仪的设计决定了采用何种旋转顺序进行姿态解算。已知由GPS测得的地面站坐标(纬度 B0、经度 L0、高度 H0),弹道坐标(纬度 Bi、经度 Li、高度Hi)和姿态测量仪测得的姿态数据(航向角 ci、俯仰角 bi、滚转角 ai)。
姿态旋转矩阵:

根据式(1)得到在火箭为原点的北东地坐标系中每个时间点地面站的位置(xi,yi,zi)。 根据式(3) (4)得到在火箭为原点的箭体坐标系中每个时间点地面站的位置(,,)。根据式(5)得到天线安装角β。
4 火箭测控系统仿真
数据输入子系统将探空火箭飞行参数数据 (如弹道参数、姿态参数)按格式要求整理以方便调用;数据处理子系统利用MATLAB软件建立地面站和火箭模型算法,加载火箭参数,运行仿真;数据输出显示子系统通过地面站对火箭跟踪性能报告和天线安装角变化范围报告实现探空火箭测控系统仿真。程序流程结构图如图4。

图4 程序流程结构图Fig.4 Program flow diagram
4.1 地面站对火箭跟踪性能结果
地面站对火箭跟踪性能结果,如图5所示,地面站A达到最大仰角81.53度时,射程43 km,高度约为313 km。地面站B达到最大仰角82.64度时,射程37 km,高度约为290 km。地面站跟踪过程中仰角最低为7度(由地面站跟踪仰角限制决定),最高约为82度,两地面站变化范围在指标要求范围内。

图5 地面站对火箭跟踪性能结果Fig.5 Results of ground stations to track the performance of the rocket
4.2 天线安装角的变化范围
分析天线安装角的变化范围是确定箭载设备天线方向图的重要依据,地面站跟踪弧段内α角在0°~180°之间变化。根据计算得到的α角和β角变化范围,在确定箭载天线方向图要求时仅考虑这个范围内的天线增益即可,如图6所示。
5 结 论
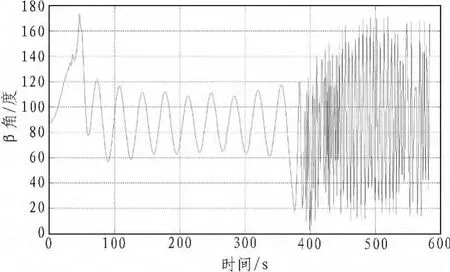
图6 天线安装角的变化范围Fig.6 The range of antenna installation angel
基于MATLAB的探空火箭测控系统仿真分析方案为弹道数据处理和测控性能分析提供了一条便捷高效的途径,提高了探空火箭任务论证的准确度和可靠性,对提高探空火箭进行科学实验的成功率,具有重要的现实意义和较高的工程参考价值。
[1]姜秀杰,刘波,于世强,等.探空火箭的发展现状及趋势[J].科技导报,2009,27(23):101-110.JIANG Xiu-jie,LIU Bo,YU Shi-qiang,et al.Development status and trend of sounding rocket [J].Science and Technology Review,2009,27(23):101-110.
[2]陈志敏,陈萍,姜秀杰,等.探空火箭有效载荷集成测试软件系统的设计与实现[J].固体火箭技术,2012,35(6):821-825.CHEN Zhi-min,CHEN Ping,JIANG Xiu-jie,et al.Design and implementation of sounding rocket payloads integrated test software system[J].Journal of Solid Rocket Technology.2012,35(6):821-825.
[3]李强,李波,杜会森.先进分布交互仿真技术在航天测控领域的应用[J].系统仿真学报,2004,16(1):175-177.LI Qiang,LI Bo,DU Hui-sen.Application of advanced distributed interactive simulation to aerospace tracking&control system[J].Journal of System Simulation,2004,16(1):175-177.
[4]丁溯泉,张波,刘世勇.STK在航天任务仿真分析中的应用[M].北京:国防工业出版社,2011.
[5]QJ2370-95弹道式导弹和运载火箭控制系统极性规定[S].北京:中国标准出版社:1995.
[6]王仲锋,杨凤宝.空间直角坐标转换大地坐标的直接解法[J].测绘工程,2010,19(2):8-9.WANG Zhong-feng,YANG Feng-bao.New study on direct calculationmethod to turn special rectangular coordinate into geodetic coordinate[J].Engineering of Surveying and Mapping,2010,19(2):8-9.
