卫星姿态控制系统的模糊控制和容错控制分配

陈 轩 ，程月华 ,姜 斌 ，贺 亮

（1.南京航空航天大学 江苏 南京 210016；2.上海航天控制工程研究所 上海 200233;3.上海市空间智能控制技术重点实验室 上海200233）

随着航天技术的不断发展，现代卫星的任务需求越来越复杂。为了提高控制系统的稳定性，需要进行容错控制设计，保证卫星在发生故障时可以顺利完成既定任务[1-2]。

卫星姿态控制系统的动态模型具有强烈的多变量耦合和非线性的特点。对于复杂系统、不确定性系统以及不能精确建模的系统而言，T-S模糊理论是进行系统建模和控制的有效工具，在航天器姿态控制领域已经取得了广泛的应用[3-4]。同时为了使卫星姿态控制系统具有满意的稳态性能和动态性能，需要将系统的闭环极点配置在复平面的特定区域内。

出于卫星运行可靠性考虑，卫星姿态控制系统通常采用冗余的执行机构配置方案。对于存在执行机构冗余的控制系统，利用控制分配方法把控制力矩分配至各个执行机构，可以实现在执行机构幅值约束下能量损耗最小、电能消耗和容错控制等控制目标[5]。但是，对于执行机构冗余配置的卫星姿态控制系统，考虑执行机构故障，在故障信息未知的情况下，研究有效的控制分配方法，确保卫星姿态控制系统正常完成任务，仍然是一个有待解决的问题。

因此，文中首先针对卫星姿态控制系统的姿态镇定问题，考虑到卫星姿态控制系统的稳态性能和动态性能，通过建立系统的T-S模糊模型，设计具有极点约束的模糊控制律。其次采用文献[6]提出的的鲁棒最小二乘方法，考虑执行机构故障造成的安装矩阵不确定性，设计了容错控制分配方法。最后，对文中研究的模糊控制和容错控制分配方法的有效性进行了数学仿真验证。

1 问题描述

为了解决卫星姿态控制系统的闭环极点配置和容错控制分配问题，首先需要对涉及的数学模型进行必要的描述。

卫星姿态控制系统的非线性动态模型为：

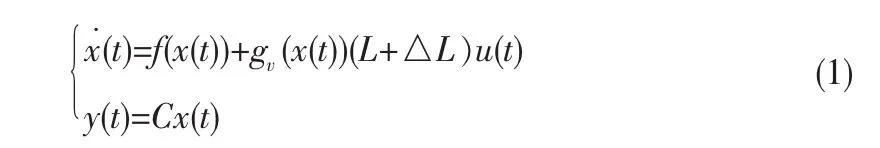
其中，系统状 态 x(t)=[φ,θ,φ,ωx,ωy,ωz]T∈R6和系 统输出y(t)=[φ,θ,φ,ωx,ωy,ωz]T∈R6为姿态角与姿态角速度，u(t)=[u1,u2,u3,u4]T∈R4为冗余执行机构的输出力矩，其约束为为系统的非线性动态特性，gv(·)为控制输入阵，L为执行机构的安装矩阵，△L为由于执行机构故障导致的安装矩阵不确定性，C=I∈R6为输出矩阵

定义三轴控制力矩为虚拟控制指令：

那么，系统(1)改写为：

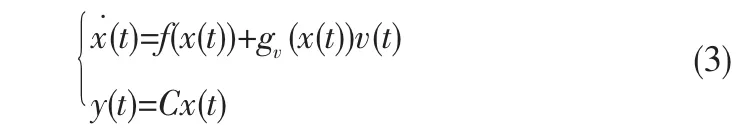
因此，卫星姿态控制系统的容错控制可以分成独立的两步：

1）针对控制力矩v(t)进行控制律设计；

2）控制力矩v(t)到执行机构输出力矩u(t)的分配。

2 模糊控制设计

首先建立卫星姿态控制系统的非线性模型(3)的T-S模糊模型，然后在此基础上进行具有极点约束的模糊控制器设计。

2.1 T-S模糊模型

T-S模糊模型通过利用一系列IF-THEN规则下的多个局部线性模型模糊逼近非线性系统。卫星姿态控制系统(3)可以由如下模糊规则描述：

2.2 具有极点约束的模糊控制

定理1针对复平面上稳定的LMI区域D

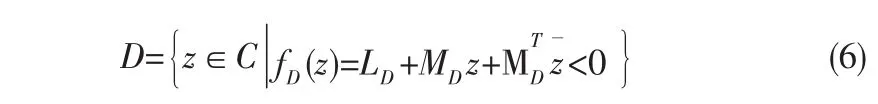
系统(5)的所有闭环极点位于LMI区域D中，当且仅当存在一个对称正定矩阵X满足

其中，A¯=[Ai+BiKi]i=1,…,r

证明：略。

注意到定理1中的不等式并非LMI，为采用MATLAB中的LMI工具箱求解，给出定理2。

定理2针对复平面上稳定的LMI区域，系统(5)的所有闭环极点位于LMI区域D中，当且仅当存在一个对称正定矩阵V和矩阵Wi满足

证明：略。

3 容错控制分配设计

对于执行机构冗余配置的卫星姿态控制系统，考虑执行机构的输出力矩约束，针对执行机构故障导致的安装矩阵不确定性，应用文献[6]提出的鲁棒最小二乘方法，将模糊控制器产生的控制力矩分配至各个执行机构。

在执行机构故障的情况下，为了使实际的三轴控制力矩与期望值的误差最小，容错控制分配问题表示为：

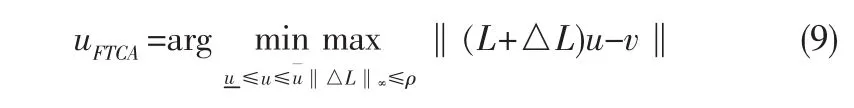
为了求解容错控制分配问题(9)，可以将其改写为二次锥规划问题：

证明：略。

4 仿真实例

为了验证本文研究的模糊控制和容错控制分配方法的

有效性，选择如下参数进行数学仿真验证：

卫星的转动惯量为：

隶属度函数如图1所示。

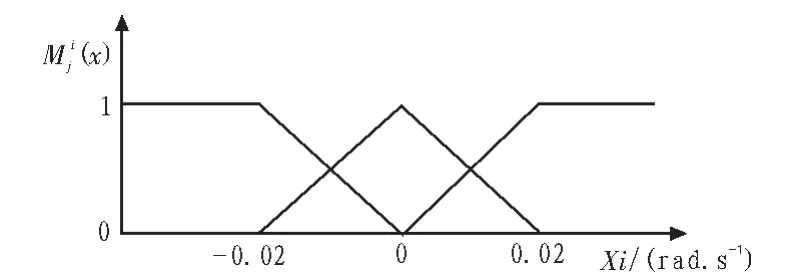
图1 隶属度函数Fig.1 Membership function

根据上述仿真参数，对文中研究的模糊控制和容错控制分配方法在MATLAB环境下进行仿真验证，仿真结果如图2～4所示。

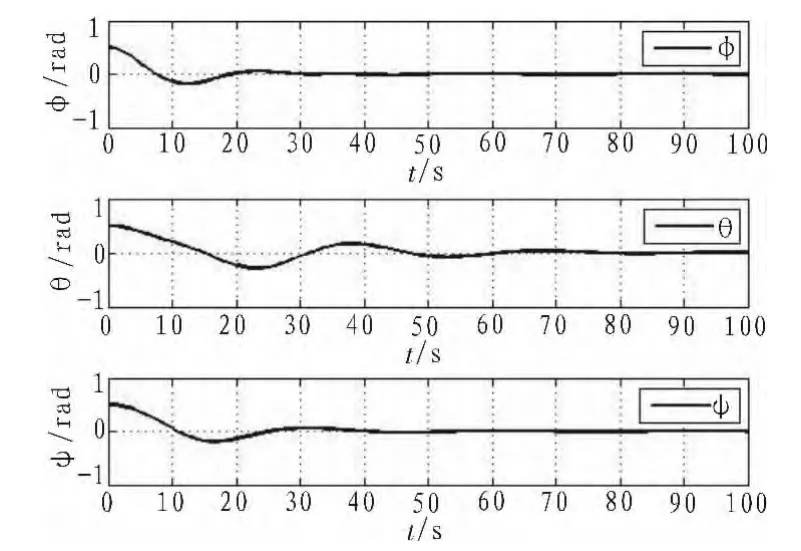
图2 姿态角响应Fig.2 Response of angular

从图2和图3可以看出，在考虑由于执行机构故障导致的安装矩阵不确定性的情况下，采用本文研究的模糊控制和容错控制分配方法可以实现卫星姿态的镇定，并且从图4可以看出，各个执行机构的输出力矩均在约束范围内。

图3 姿态角速度响应Fig.3 Response of angular velocity

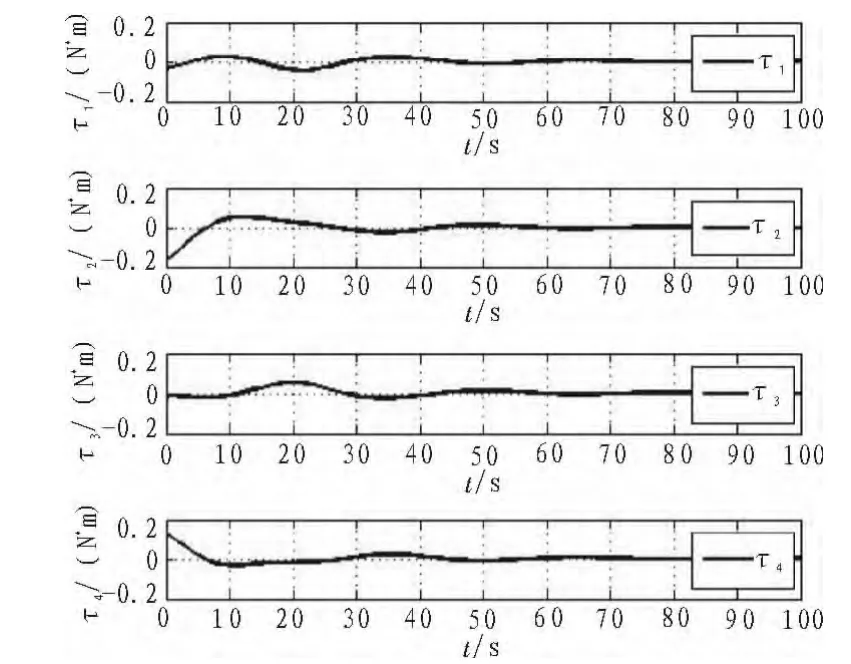
图4 执行机构输出力矩响应Fig.4 Response of control torque

5 结论

文中研究了执行机构冗余配置的卫星姿态控制系统的姿态镇定问题。针对系统非线性模型的区域极点配置，通过建立系统的T-S模糊模型，设计了具有极点约束的模糊控制律。同时对于执行机构故障引起的安装矩阵不确定性，应用鲁棒最小二乘方法，实现控制力矩到执行机构输出力矩的容错控制分配。最后仿真验证了本文研究的模糊控制和容错控制分配方法的可行性，仿真结果表明该方法在执行机构故障情况下仍然可以实现姿态镇定，并且具有良好的动态特性。

[1]张娴,程月华,姜斌.轨控期间挠性卫星姿控系统的容错控制[J].航天控制,2011,29(1):41-47.ZHANG Xian,CHENG Yue-hua,JIANG Bin.Adaptive backstepping fault-tolerant control for flexible satellite attitude control system during orbit control[J].Aerospace Control,2011,29(1):41-47.

[2]王剑非,姜斌,冒泽慧.基于LSSVM的卫星姿态控制系统故障诊断[J].控制工程,2008,15(3):334-341.WANG Jian-fei,JIANG Bin,MAO Ze-hui.LSSVM based fault diagnosis for satellite attitude control system[J].Control Engineering of China,2008,15(3):334-341.

[3]樊雯,程月华,姜斌.基于模糊滑模的卫星姿态控制系统故障诊断[J].东南大学学报:自然科学版,2010,40(增刊):238-243.FANWen,CHENG Yue-hua,JIANG Bin.Fault diagnosis in attitude control system of satellite based on fuzzy sliding mode [J].Journal of Southeast University:Natural Science Edition,2010,40(Sup):238-243.

[4]王玉惠,吴庆宪,姜长生,等.具有极点约束的空天飞行器再入姿态的H∞模糊保性能控制[J].信息与控制,2008,37(3):298-304.WANG Yu-hui,WU Qing-xian,JIANG Chang-sheng,et al.H∞fuzzy guaranteed cost control with pole constraints for aerospace vehicle’s re-entry attitude[J].Information and Control.2008,37(3):298-304.

[5]FU Yan-ping,CHENG Yue-hua,JIANG Bin,et al.Fault tolerant control with on-line control allocation for flexible satellite attitude control system[C].International Conference on Intelligent Control and Information Processing,2011.

[6]Ghaoui L E,Lebret H.Roubust solution to least squares problemswith uncertain data[J].SIAM Journal on Matrix