基于FDTD的环形孔缝电磁耦合规律研究
2014-03-16孙延鹏安小鹤孙红鹏孙立威
孙延鹏,安小鹤 ,孙红鹏,孙立威
(1.沈阳航空航天大学 电子信息工程学院,辽宁 沈阳110136;2.沈阳飞机设计研究所 辽宁 沈阳 110035)
电子技术的迅速发展显著提高了各类电子系统的性能,却也带来了更加复杂的电磁环境。为防止电磁脉冲对电子系统造成损害,屏蔽腔常被用来屏蔽电磁辐射以保护电子设备。电子设备需要显示数据以及与外界电路传输信号等,腔体上就必然存在如舱门、铆钉缝等规则与不规则形式的孔缝。电磁脉冲由缝隙或孔洞耦合进入腔体对电子设备造成危害,从而影响电子系统的功能。因此,对各类孔缝与电磁脉冲的耦合问题的研究也变得更加重要。
小孔的耦合理论在1944年被H.A.Bethe提出[1],后来R.F.Harrington利用矩量法(MOM)对孔缝的耦合进行了研究[2]。学者们已经应用了多种方法对带有孔缝腔体的耦合规律做了研究,如时域有限差分方法(FDTD)[3],有限元法[4]等。由于电磁脉冲通过孔缝的耦合问题是瞬态的电磁场问题,FDTD方法常被用来对其进行模拟数值分析。当前针对孔缝耦合的研究中,研究对象大多是正方形、矩形之类的规则孔缝[5-6],而对实际中普遍存在的如铆钉缝、舱门缝之类的环形孔缝等不规则孔缝的研究则很少涉及。本文利用三维FDTD方法分析了电磁脉冲对方形环、圆环及矩形环的耦合特性。
1 计算模型与理论
1.1 腔体模型
屏蔽腔体模型如图1所示,材质为理想导体。屏蔽腔体为边长20 cm的正方体,腔体壁厚度为2mm。腔体位于入射电磁波的远场区域。
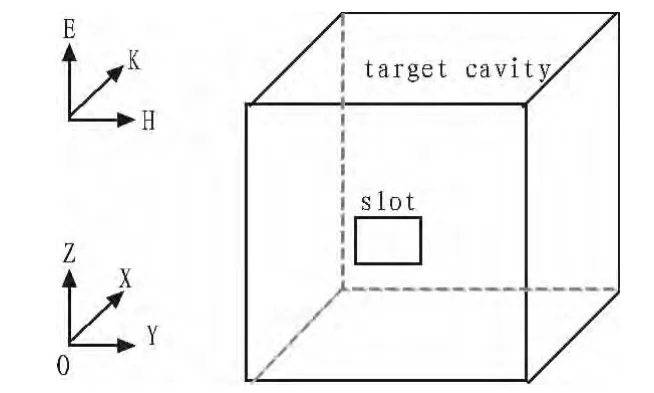
图1 腔体模型Fig.1 Shielded cavitymodel
本文中所采用的环形孔形状分别为圆环,方形环及矩形环。孔缝几何中心位于面中心处,电磁脉冲沿轴方向垂直于面射向腔体。为比较不同形状环形孔缝对于电磁耦合的影响,各种环形孔面积大小一致。由于舱门缝、铆钉缝等环形孔缝一般都在mm量级,因此选取环形孔缝环宽均为2 mm,面积为200mm2。环形孔缝模型如图2所示。
1.2 三维FDTD计算原理
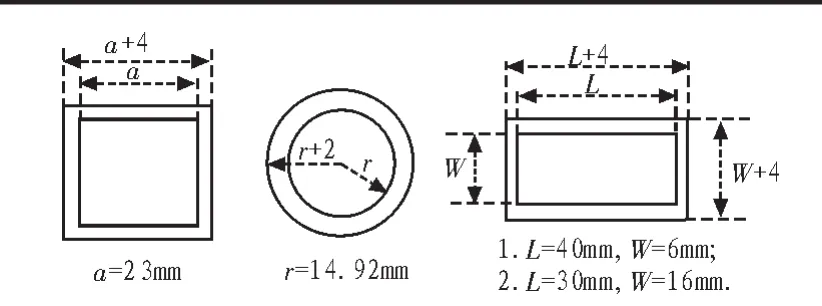
图2 环形孔缝模型Fig.2 Annular aperturemodel
Maxwell方程组是电磁场问题中的基本方程[7],三维FDTD方法是利用Yee元胞对三维空间模型划分网格,然后对微分形式的麦克斯韦方程进行二阶中心差分离散,从而得到时域上的递推公式,然后利用给定电磁场初值及边界条件,求解出空间中各个时刻的电磁场数值。直角坐标系下微分形式的Maxwell方程为
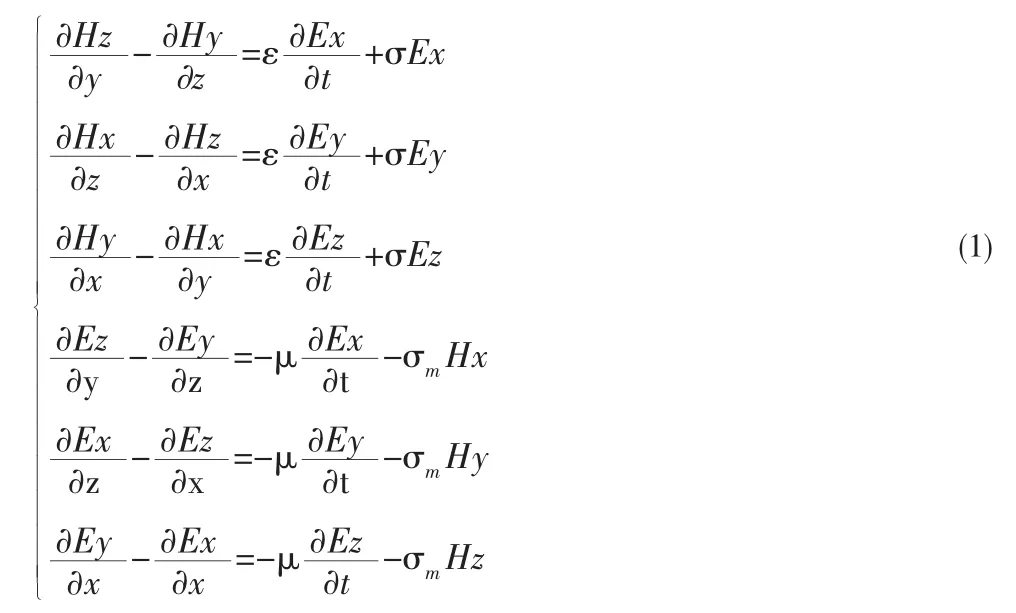
其中ε为介质中的介电常数,μ为介质磁导系数,σ与σm分别为介质的电导率与导磁率。、Ex、Ey和Ez及Hx、Hy和Hz分别表示三维条件下电磁场在直角坐标系中各个方向的电场与磁场分量。

式(2)及(3)中、△x、△y及△x为所划分三维空间网格在x、y及z方向上的网格长度,为在时间上离散的时间步长。利用此迭代方程组,设置PML吸收边界条件,结合给定的电场初值,可求得各个时刻各个位置的电场及磁场大小。为了使所求解结果收敛稳定,时间步长与网格大小应满足Courant条件:

对空间中各个点处时域电场进行快速傅里叶变换可得电场随频率的变化特性,由此将屏蔽系数定义为:
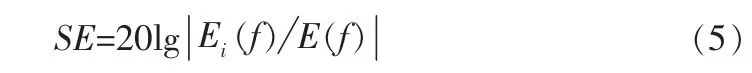
Ei(f)与 E(f)分别为对电子系统加屏蔽体与不加屏蔽体时同一点处的随频率变化的电场强度。
矩形谐振腔的谐振波长及频率为[8]:
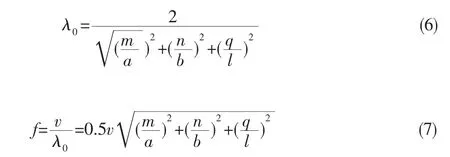
上式中谐振腔的尺寸为 a×b×l;m、n和q分别为场量在x、y和z轴上分布半波的数目,m n q取值不同,则其所对应的的谐振波模式也不同。
1.3 激励源
目前,电磁脉冲激励源有多种类型,如快前沿电磁脉冲、超宽带(UWB)电磁脉冲等[9]。相对于另外其他电磁脉冲,超宽带脉冲具有极宽的频带,且不使用载波,耗电量低,其对电子系统的危害较大。因此,本文用高斯函数来模拟超宽带脉冲作为本文的激励源,其表达式为:

式中E0为脉冲峰值,t0与τ分别决定了脉冲出现最大值的时间及脉宽大小。 本文选取 E0=1 000 V/m,τ=9.4×10-11,t0=1.23×10-10。其脉冲宽度约为85 ps,其频带极宽,能很好的表征超宽带脉冲。设入射脉冲极化方向为垂直,电场为z方向。
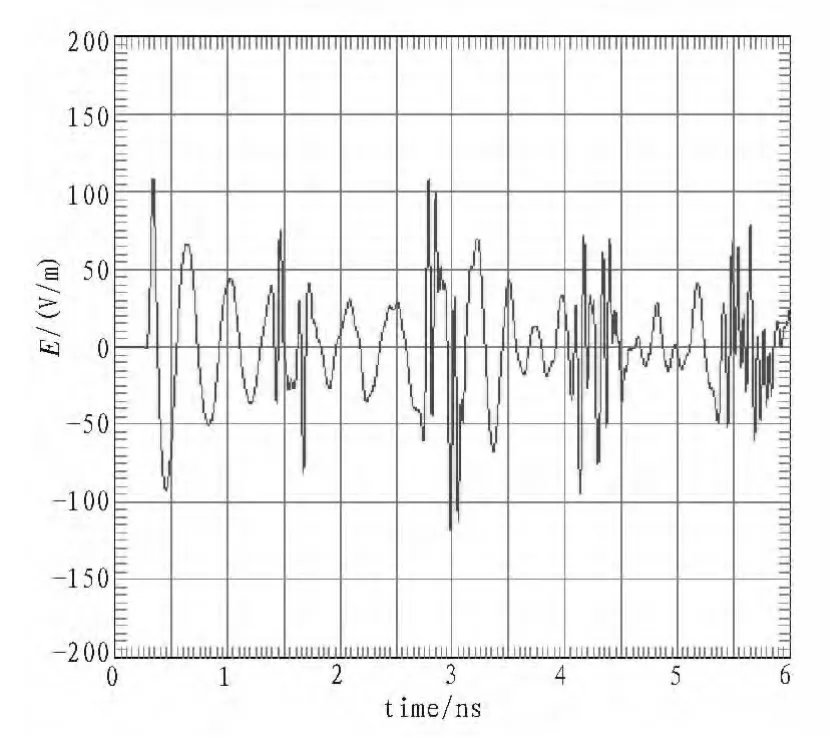
图3 带圆环腔体内距孔缝3 cm处电场Fig.3 Electric field of the place 3 cm to circular annular aperture in the cavity
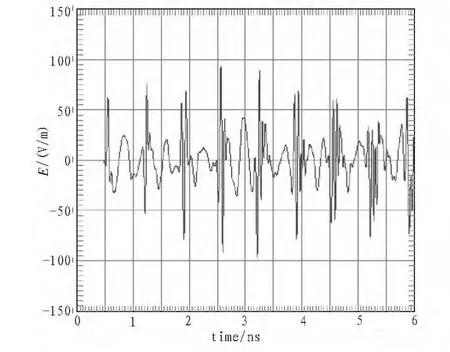
图4 带圆环腔体中心耦合电场Fig.4 Electric field of the center of the cavity with circular annular aperture
2 实验结果及分析
在环形孔缝的面积保持一致的情况下,对不同脉宽的电磁脉冲与不同形状的环形孔缝的耦合规律进行了仿真分析。
2.1 圆环与电磁脉冲的耦合规律
图3、图4分别是带圆环腔体中心与腔体环形孔缝轴线上距孔缝3 cm处时域电场波形。观察图3、图4,由于腔体壁对电磁脉冲的反射,电磁脉冲通过环形孔缝在腔体内部发生有规律的振动,耦合电场波形振荡周期分别约为1.13 ns和0.67 ns,此与数值计算的脉冲分别由腔体内3 cm处及腔体中心处传播至腔体壁再反射回来的时间一致。由此可知,图中首个脉冲即为耦合电场的主脉冲,随后的脉冲为主脉冲经过腔体壁反射回来的脉冲。电场主脉冲之后的一段脉冲的电场强度明显增大是由于腔体内部反射脉冲的叠加。但同时电磁波在腔体内部传输时会通过孔缝向外传播辐射,因此在随后的耦合电场幅度会有所衰减。电磁波在传播过程中会消耗能量,造成衰减,因此图3中耦合主脉冲的电场幅度比图4中的大。
2.2 方形环与电磁脉冲的耦合规律
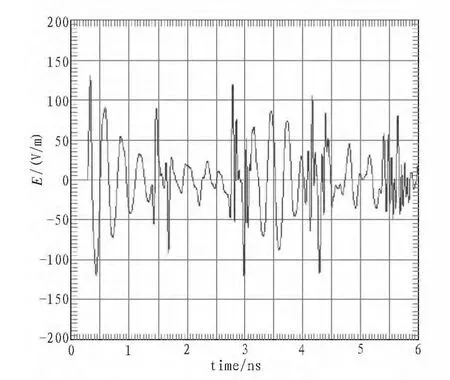
图5 带方形环腔体内距孔缝3 cm处电场Fig.5 Electric field of the place 3 cm to square annular aperture in the cavity
图5是带方形环腔体内距孔缝3 cm处时域电场波形。对比图5与图3,方形环的耦合规律与圆环的规律非常相似,但通过方形环的脉冲耦合电场幅度略大于圆环。由此可知,带圆环的腔体的屏蔽效果要略强于带方形环的腔体。
对腔体中心时域电场进行快速傅里叶变换,得到电场在频域的变化波形,如图6所示。图中第一个谐振频率点约在1.07 GHz频率位置,与公式(7)所计算出的一致。在各个谐振频率点处频域电场峰值达到最大,因此腔体在谐振点处屏蔽蔽效果很差。在3~6GHz高频率段,频域电场强度比低频部分要大,可知高频成分较易通过方形环孔缝,在高频段腔体的屏蔽效能非常差。

图6 带方形环腔体中心频域电场Fig.6 Electric field in frequency domain of the center of the cavity with square annular aperture
2.3 不同纵横比矩形环的耦合规律
为了解纵横比对矩形环孔缝与电磁脉冲耦合规律的影响,选取3种面积相同但纵横比不同的矩形环孔缝,其长宽为L=40 mm,W=6 mm;L=30 mm,W=16 mm;L=23mm,W=23mm,面积200mm2,如图 2所示。图7、图8分别为在入射脉冲电场垂直极化与水平极化情况下腔体内距孔缝3 cm处不同长宽比矩形环与电磁脉冲的耦合电场波形。由图可知,在电场极化方向垂直于矩形环长边时,随着长宽比越大,则耦合进入腔体的能量越大,电磁脉冲越容易耦合进入腔体;而在电场极化方向平行于矩形环长边时,随着长宽比越大,耦合进入腔体的能量却越小。对于23×23的方形环及圆环,垂直极化与水平极化情况下电场耦合能量相同,说明对于正对称形状的孔缝,电场极化方向不影响其耦合规律。
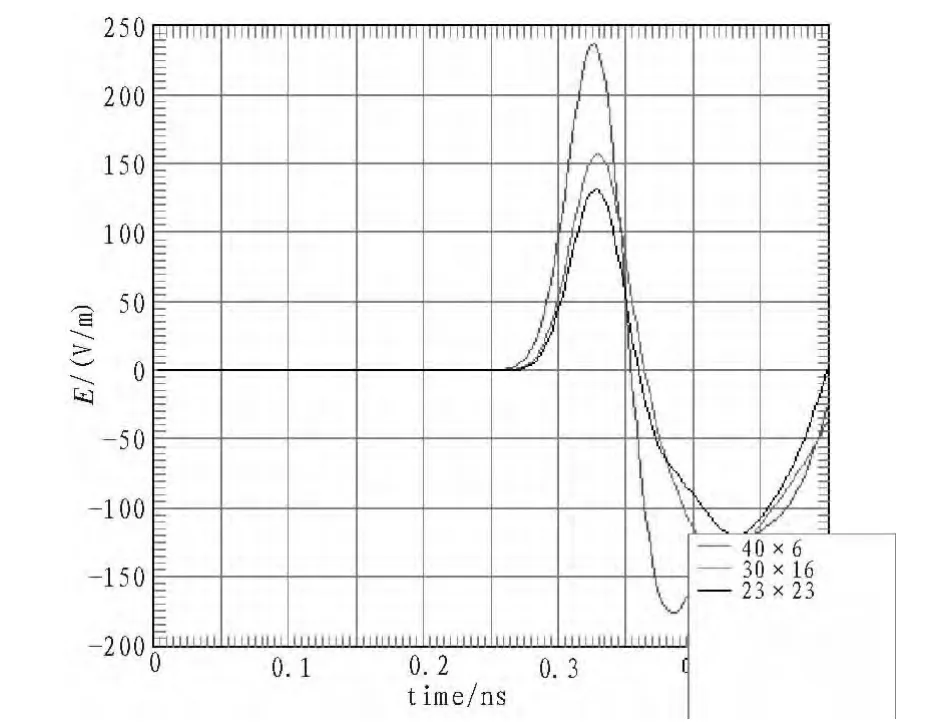
图7 垂直极化时不同长宽比矩形环腔体内部距孔缝3 cm处对比Fig.7 Comparison figure of the electric field in the place 3cm to the aperture with different respect ratio when the electric is perpendicular to the long side of the aperture

图8 水平极化时不同长宽比矩形环腔体内部距孔缝3cm处对比Fig.8 Comparison figure of the electric field in the place 3cm to the aperturewith different respect ratiowhen the electric is parallel to the long side of the aperture
2.4 入射波脉冲宽度对耦合规律的影响
选取脉冲宽度分别为 220 ps、330 ps、470 ps及550 ps的高斯脉冲射向方形环孔缝,其腔体内中心点处电场波形如图9所示。由图可知,当脉宽为220 ps时,其通过方形环的耦合电场强度最大,而当脉宽为550 ps时,其耦合电场最小。由此可知,当入射脉冲的脉宽越小时,电磁波就越容易与环形孔缝发生耦合。

图9 不同脉宽脉冲入射时腔体内中心时域电场Fig.9 Electric field of the center in the cavity when pulse width is different
2.5 垂直极化时不同入射角度影响
选取圆环环孔缝为研究模型,以高斯脉冲为激励源,在电场垂直于孔缝长边情况下,以入射波方向与小孔所在平面法线方向夹角定义入射角度, 分别选取 0°、30°、45°、60°及90°入射。为方便观察,截取1 ns波形进行分析,如图10所示。由图可知,在入射夹角为0°时电场内部耦合能量最大,而随着角度增大,电场强度逐渐减小,90°时最小。因此,在电场垂直极化情况下,入射脉冲与孔缝所在平面法线方向夹角越小,则耦合能量越大,腔体的屏蔽效果也就越差。

图10 垂直极化时不同入射角度脉冲耦合电场比较Fig.10 Comparison of the electric field of the incident pulse with different incident angle coupling into the annular aperture when the electric is perpendicular to the long side of the annular aperture
3 结论
本文采用三维FDTD[10-11]方法对带有环形孔的腔体与电磁脉冲的耦合规律进行了研究,分析了不同类型环形孔与不同脉宽电磁脉冲的耦合规律。研究发现,电磁脉冲与环形孔耦合现象明显,其通过环形孔在腔体内部发生有规律的振动。利用腔体能很好的屏蔽电磁波,但矩形腔体谐振频率点处的屏蔽效果非常差,在实际应用中应使各类电子设备工作频率远离谐振频率。对于孔缝面积一致的3种环形孔缝(方形环,矩形环和圆环),在垂直极化情况下,电磁脉冲通过方形环与圆环耦合的能量明显小于矩形环,圆环略小于方形环。入射脉冲高频成分较易通过方形环孔。当入射波极化方向与矩形环短边平行时,矩形环孔缝的纵横比越大,则电磁波就越容易与矩形环耦合从而进入腔体内部;而当入射波电场极化方向与矩形环短边垂直时,矩形环孔缝的纵横比越小,电磁波越容易与矩形环耦合进入腔体内部。当入射脉冲的脉宽越小时,电磁波就越容易与环形孔缝发生耦合。电场极化方向垂直于矩形环长边时,随着入射脉冲方向与孔缝所在平面法线夹角越小,耦合进入腔体的能量越大,对腔体内部设备的危害也就越大。本文所得环形孔缝的耦合规律结论对于提高电子[12]系统的工作性能具有重要意义。
[1]Bethe H A.Theory of diffraction by small holes[J].Phys.Rev,1944,66(10):163-182.
[2]Harrington R F,Mautz JR.A generalized networkformulation for aperture problems[J].IEEE Trans on Antennas and Propagation,1976,26(3):870-874.
[3]Georgakopoulos SV,Birtcher CR,Balanis C A.HIRF penetration through apertures:FDTD Versus Measurements[J].IEEE Trans on Electromagnetic Compatibility,2001,43(3):282-294.
[4]Nuno L,Balbastre JV,Castane H.Analysis of general lossy inhomogeneous and anisotropic waveguides by the finiteelementmethod(FEM)using edge elements[J].IEEE Trans on Microwave Theory and Techniques,1997,45(3):446-449.
[5]肖金石,刘文华,张世英,等.超宽带电磁脉冲对腔体孔缝耦合效应的数值模拟[J].强激光与粒子束,2010,22(12):2959-2963.XIAO Jin-shi,LIUWen-hua,ZHANG Shi-ying,etal.Numerical simulation on coupling effects of ultrawide band electromagnetic pulse into slots in a cavity[J].High Power Laser and Particle Beams,2010,22(12):2959-2963.
[6]周金山,刘国治,王建国.矩形孔缝耦合特性实验研究 [J].强激光与粒子束,2003,15(12):1228-1232.ZHOU Jin-shan,LIU Guo-zhi,WANG Jian-guo Experimental studies on coupling characteristics of rectangular slot[J].High Power Laser and Particle Beams,2003,15(12):1228-1232.
[7]葛德彪,闫玉波.电磁波时域有限差分方法 [M].西安:西安电子科技大学出版社,2002.
[8]高建平.电磁波工程基础 [M].西安:西北工业大学出版社,2008.
[9]刘顺坤,傅君眉,周辉,等.电磁脉冲对目标腔体孔缝耦合效应数值研究 [J].电波科学学报,1999,14(2):202-206.LIU Shun-kun,FU Jun-mei,ZHOU hui,etal.Numerical studies on coupling effects of EMP into slots[J].Chinese Journal of Radio Science,1999.14(2):202-206.
[10]覃宇建,王为,周东明,等.基于TDIE-FDTD混合算法的电磁环境效应分析[J].现代电子技术,2013(21):157-162.QIN Yu-jian,WANGWei,ZHOU Dong-ming,et al.Analysis of electromagnetic environmenteffect based on TDIE-FDTD hybrid algorithm[J].Modern Electronics Technique,2013(21):157-162.
[11]黄斌科,张爽.FDTD方法分析THz波段金属平板的屏蔽特性[J].电子科技,2013(2):129-132.HUANG Bin-ke,ZHANG Shuang.Analysis of shielding characteristics ofmetal slab at THz frequencies using FDTD method[J].Electronic Science and Technology,2013(2):129-132.
[12]王建国.真空电子器件的粒子模拟方法[J].现代应用物理,2013(3):251-262.WANG Jian-guo.Particle simulationmethod of vacuum electronic devices[J].Modern Applied Physics,2013(3):251-262.
