基于并行动态无功优化蚁群算法的应用

周鑫,刘柱揆,许守东

(云南电网公司电力研究院,昆明 650217)

基于并行动态无功优化蚁群算法的应用

周鑫,刘柱揆,许守东

(云南电网公司电力研究院,昆明 650217)

为考虑负荷变动下动态无功优化控制变量全天动作次数的限制,针对其多目标、强时空耦合的特点,以全天电能损耗最小、变压器分接头和电容器投切次数最少为目标函数,通过改进调节变量动作的时间约束,提出一种更加实用的新模型。利用并行算法计算不同目标函数,并通过多种信息素交换方可得到多组的较优解,增加了算法的灵活性和实用性。本文蚁群算法在寻优过程中不仅计及整个网络电能损耗的减少,而且改进了蚁群间信息素交换规则,因此能够较快地找到对电能损耗影响较大的节点,提高搜索速度。通过IEEE14、IEEE30系统仿真计算验证了该模型及算法的有效性和可行性。结果表明该文模型及算法能够有效的调节及分配控制变量的动作次数,对调节时机的选择也更为准确。

动态无功优化;并行蚁群算法;多目标

1 前言

电力系统动态无功优化中不仅需要考虑系统全天负荷的变动,还要满足控制设备动作次数的要求。所以,其是一个大规模、非线性、多时段的混合整数规划。由于问题本身的复杂性和矛盾性,电网在实际运行中往往是根据经验安排全天的动作时间及次数。因此,如何在保证电能质量的前提下通过合理控制变压器分接头和并联电容器投切,引起了众多研究人员的兴趣。

目前,电力系统动态无功优化目标函数主要为在满足动作次数的约束条件下使电网全天电能损耗最小[1-8]。在此基础上,文献 [9]针对电力市场下无功服务的特点,以有功网损电费和无功辅助服务费用的总和最小为目标,提出了计及无功费用的日无功计划数学模型。

在求解策略上主要通过数学方法及进化算法[10-15]仿真分析。文献 [11-12]应用内嵌离散惩罚机制的非线性原对偶内点法求解动态无功优化问题,较好的解决内点法求解时存在维数灾的问题。文献 [13]提出一种改进的禁忌搜索算法,将时间段的起始点和该段控制变量共同构成解向量,达到整体上优化的效果。文献 [14]根据设备的寿命将动作次数转化为经济成本,保证的经济效益,但这样调节可能无法有效的提高电网的电能质量,不能满足电网的实际需要。文献[15]将一天24h的负荷曲线按照剧烈程度分为相应的阶梯状分布曲线,各分段对采用静态无功优化,有效的减少了计算时间。但是静态分时段方法无法很好的从全局上考虑每次设备动作的效果,全局寻优能力较弱。

文中首先根据我国110 kV及以上变压器分接头全天动作次数需少于10次的规定[16-17],对模型进行了研究,提出一种具有时间约束的新多目标模型。然后针对该模型对多种群蚁群算法进行讨论,建立了一套新的搜索策略和信息交换规则,使蚁群能够更加容易的得到多个全局最优解,为实际系统的运行增加了灵活性。

2 多目标动态无功优化的数学模型

动态无功优化是一个多目标问题,单目标算法无法从整体上考虑动态无功优化的要求。为了提高电网运行的可靠性、安全性、灵活性。本文选取系统全天电能损耗最小和调节设备动作次数最少为目标函数,并改进了调节设备动作的时间约束,其目标函数及约束条件表示如下：

(1)目标函数

minF=(f1,f2) (1)

(2)约束条件[7]

PGi-PLi-Ui∑nj=1Uj(Gijcosδij+Bijsinδij)=0 (2)

QGi-QLi-Ui∑nj=1Uj(Gijsinδij-Bij-Bijcosδij)=0 (3)

QGimin≤QGi≤QGimax(4)

Vimin≤Vi≤Vimax(5)

QCimin≤QCi≤QCimax(6)

Timin≤Ti≤Timax(7)

式中：f1=min∑23i=0Ploss,t(Vt,Qt,Tt)Δt为系统全天电能损耗;f2=min∑23t=0(Tl,t⊕Tl,t+1|,|Cm,t⊕Cm,t+1|)为控制设备全天动作次数;PGi(QGi)、PLi(QLi)、Ui、Gij、Bij、δij分别为节点i的发电机有功(无功)出力、有功(无功)负荷、节点i电压、节点i与节点j间电导和电纳以及节点间的电压相角差;QGimin(QGimax)、Vimin(Vimax)、Qcimin(Qcimax)、Timin(Timax)分别为发电机注入无功、节点电压幅值、并联电容器无功容量、变压器变比的最小(最大)值。

电力系统动态无功优化主要是根据各时段负荷水平调节控制设备的状态,使系统的全天电能损耗达到最小。但考虑到电容器开关和OLTC分接头等离散控制变量的使用寿命,必须对它们的全天动作次数进行限制。由于不同时段间控制设备的调节效率,与该时段负荷变化率幅度相关[18]。但文献[18]对离散控制设备动作区间是优化初期就确定的,没有根据控制设备的动作情况对其进行调整,而且相关参数是通过仿真得到,对于不同系统需重新进行计算,增加了优化过程的难度和工作量。因此,本文提出动态调整离散控制设备动作区间约束条件的方法。

在对每个时段优化时,首先根据各控制设备剩余的调整次数及之后时段的负荷率差值,重新计算当前时段的控制设备可动作次数,如式(8)～(10)。

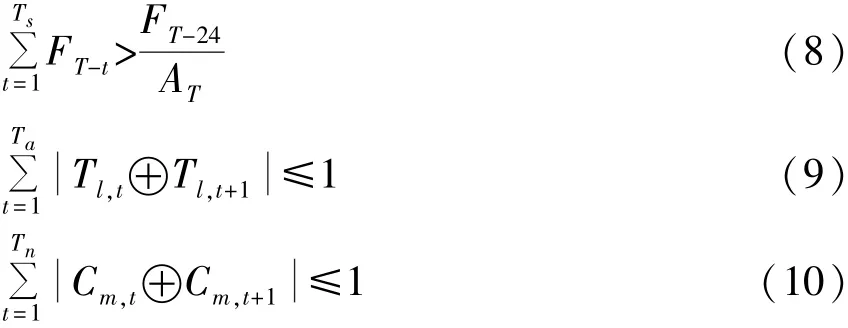
式中：FT-t为T-t时段的负荷率差值;Ts表示T时段无需动作时间,分别对应于式(9)、(10)中的Ta、Tn;AT为T时段离散控制设备总剩余可动作次数,每一时段优化后均对其进行计算;Tl,t为第l个变压器分接头t时段的档位值,式(9)表示只允许变压器分接头在Ta个相邻时段动作一次,本文认为分接头每调节一档即动作一次。Cm,t为第m个电容器开关t时段的状态,式(10)表示只允许电容器在Ts个相邻时段动作一次,本文采用实际变电站电容器“先投先切、后投后切”的原则[19],并对不同精度的目标设定不同的时间间隔。

3 蚁群算法求解策略

3.1 蚁群算法[20]

蚂蚁优化算法本身是一种迭代算法,但它并不是简单的迭代,当前的迭代总是利用以前迭代的信息,即模拟了信息正反馈原理。由于正反馈原理和启发式算法相互作用,使得蚁群算法有着较强的全局收敛性,并在解决TSP问题中的到了验证。

3.2 启发因子选择

为了反映各控制变量对总电能损耗变化的影响程度,本文选取电容器无功对电能损耗的灵敏度[21]及流过变压器的电流为能见度因子。

3.3 基于双种群蚁群算法的动态无功优化

本文在蚁群算法具有内在的并行性和加强学习的特点的基础上,结合动态无功优化的特点采用改进的双种群蚁群算法,运用不同的蚂蚁种群分别计算两个不同的目标函数,并根据所需可行解的个数自动调整约束条件的数值从而得到几组可行解,增加了运行地灵活性。

3.3.1 目标函数的转化

本文把动态无功优化问题设计成类似于TSP (Traveling Salesman Problem)问题的模式,并适当的处理约束条件,从而使该问题可以运用蚁群算法求解。蚂蚁优化算法中,每个优化方案均由一只蚂蚁走过的路径表示。每次优化的所有状态对应于TSP问题中的各个城市,而两个状态之间的决策对应于TSP中直接连接两个城市的路径。相应的目标函数式(1)中的f1、f2可以分别写成TSP问题模式：

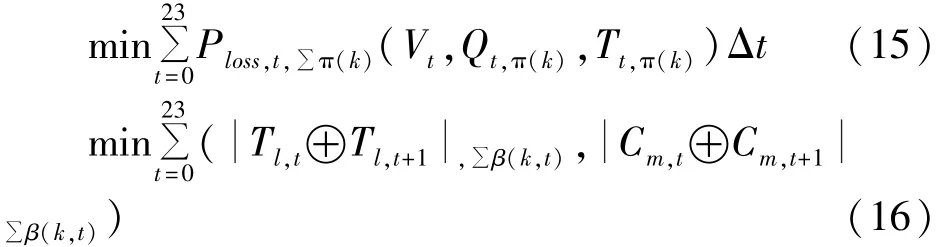
式中：π(k)代表每只蚂蚁在第k次调节控制设备时选择的状态集合;Qt,π(k)、 Tt,π(k)分别代表在t时段对应的补偿容量及变压器分接头的变比向量的状态集合;∑β(k,t)代表每只蚂蚁在t时刻第k次调节控制设备时设备的调节次数的状态集合。

3.3.2 信息素更新规则

本文采用与文献 [18]相同的单种群蚁群算法状态转移概论和搜索策略,并对种群间信息素交换方式进行改进,为了保持种群的多样性在更新过程中需要考虑每个控制变量的种群密度系数如式(21)、(22)所示[22];在一次搜索完成之后,则加强上次搜索的较优信息素浓度。假设现有n个控制变量。

式中：Dj,k表示控制变量j在第k次调节设备时的动作次数;fk为控制变量k的种群密度;(t)为蚂蚁第k次调节时节点t的信息素;ek表示多样性系数随搜索次数的增长影响度成指数增长;β、χ为常数。τij(t+n)表示完成一次搜索后节点的信息素;Di为控制变量在上次搜索过程中所动作的次数。

为了使不同种群在不同时间段能有效的收敛于最优解,本文采用信息素的横向交换和纵向更新规则[22],并对其进行改进。在每次搜索开始前读取以前时段的相应最优解的信息素浓度,并在搜索完成后,对不同种群之间相应的最优解进行信息交换。(22)

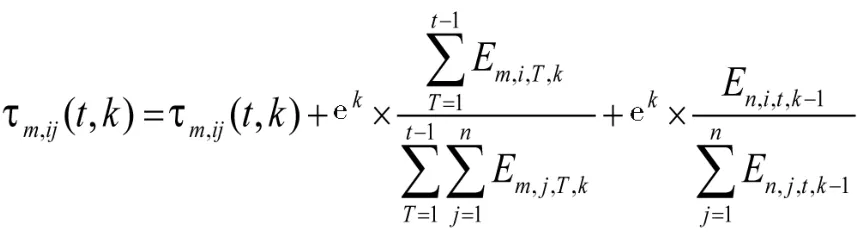
式中：τm,ij(t,k)为种群m在t时刻第k组可行解中控制变量 i的信息素初始浓度Em,i,T,k为种群m在t时刻以前控制变量i在第k组最优解中的动作次数;En,i,t,k-1为种群n在t时刻控制变量在第k-1组最优解中的动作次数。e为常数,表示两个种群的信息交换量随着寻优过程逐渐增加。

3.3.3 并行蚁群算法流程图

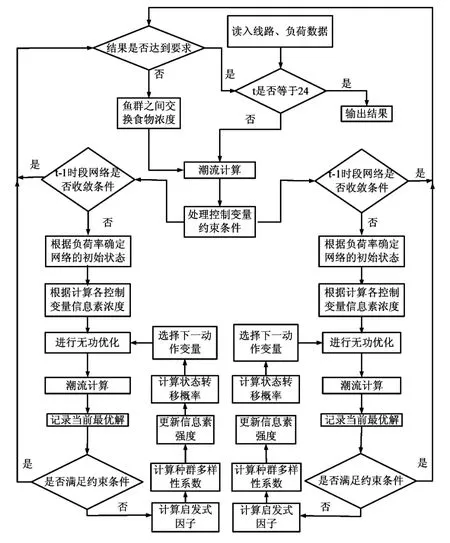
图1 并行蚁群算法的动态无功优化流程图

4 算例分析

文中计算程序采用Matlab7.0环境编制,采用IEEE14[23]、IEEE30[19]节点,对所建模型与算法进行仿真。全天24h负荷曲线如下图2所示：

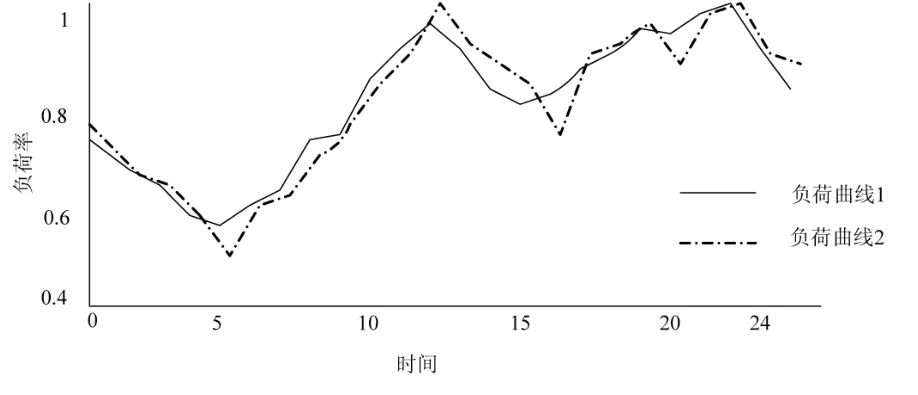
图2 系统负荷率分布曲线

4.1 调节设备动作时间约束的影响

以文中模型算法、文献 [23]模型算法、无时间约束模型为例,全天能耗最小为目标函数,对表1、表2分别采用负荷曲线1、2,对IEEE14测试系统进行仿真计算。

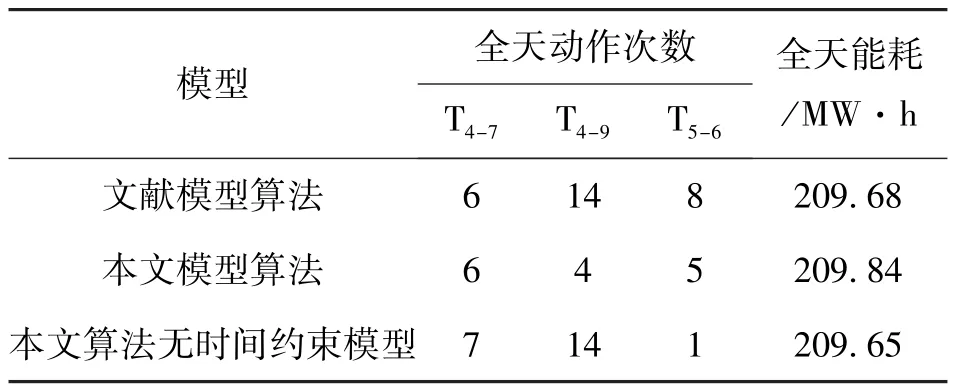
表1 IEEE14系统3种模型下的动态无功优化结果

表2 IEEE14系统2种模型下的动态无功优化结果

从表1中可以看出,若采用文献模型及算法, IEEE14系统3组变压器分接头全天动作次数分别为6、14、8。在多种群蚁群算法无时间约束模型条件下,变压器全天调节次数分别为7、14、1,动作总次数相比较少,但全天电能损耗略小,说明本文算法在动作时间及动作幅度的选择上更为准确,能够有效的收敛于全局最优解。

但结果仍无法满足系统实际运行中变压器全天动作次数需少于10次的要求,通过分析表1、表2可以得知,在两种负荷条件下,与文献模型、无时间约束模型相比,本文模型仿真结果全天电能损耗分别增加0.16 MW·h、0.19 MW·h、0.09 MW·h,而变压器的动作次数明显减少,各变压器调节时间和调节次数也更加均匀,可以有效减少变压器在短时间内产生的电弧,使其有充分的冷却时间,延长变压器寿命。

4.2 多目标结果的分析计算

采用文中提出的多目标模型的多种群蚁群算法以全天电能损耗最小、变压器分接头和电容器投切次数最少为目标函数,每个种群得到3组解为条件,对IEEE14、IEEE30测试系统进行仿真,部分计算结果见表3、表4。

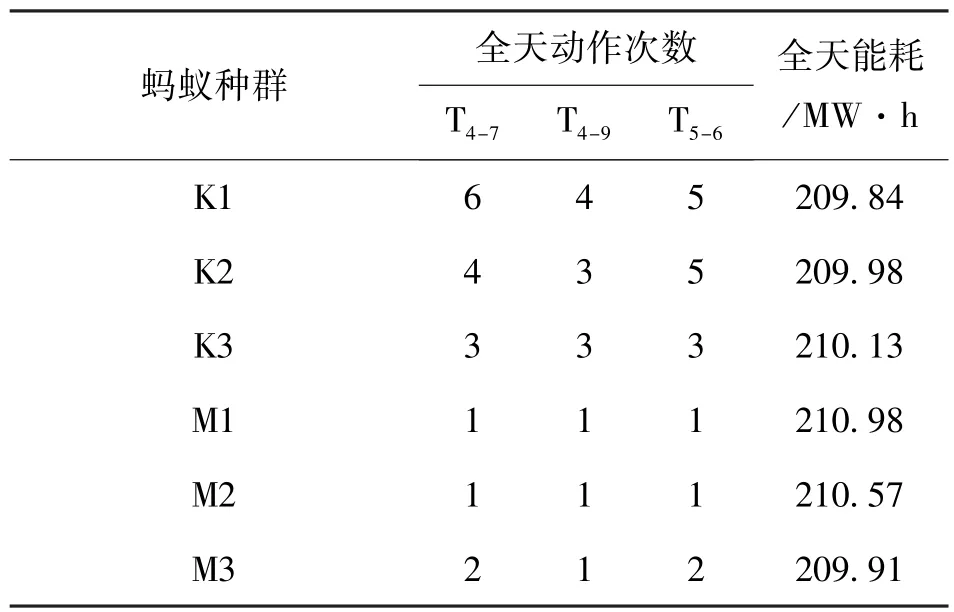
表3 多种群蚁群算法IEEE14优化结果

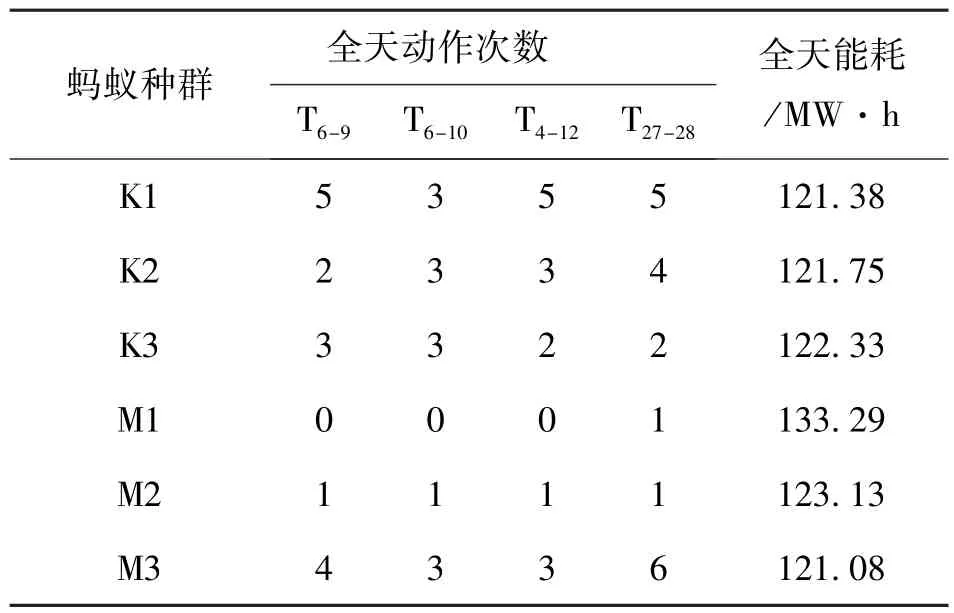
表4 多种群蚁群算法IEEE30节点优化结果

表3为IEEE14节点仿真计算结果,K、M分别代表蚂蚁种群1、2。从表3中可以得出种群1的优化结果随着变压器分接头的减少全天能耗也随之变化。种群2中M1、M2动作次数相同而全天能耗的不同。从M3与K2对比可以发现,M3的动作次数相对较少但效果较好。分析表4同样可以发现,M3与K1相比动作总次数少一次,优化效果却较好。通过分析有两点原因,1.电容器动作次数及补偿容量的不同;2.两个种群通过交换信息素互相学习加强了蚁群算法的全局寻优性能。在本文多目标算法中可以根据需要可以得到不同目标函数的几组近似解,从而能够为系统的实际运行提供了不同的方案。

5 结束语

本文建立了动态无功优化的新模型,提出了一种新的双种群蚁群算法,通过对 IEEE14、IEEE30系统进行仿真计算,结果验证了模型及算法的正确性、有效性,并得出如下结论：

1)模型考虑了动态调节设备的动作时间约束,能够有效的保证变压器全天的动作次数要求,并可以更加合理的分配分配变压器、电容器动作次数。

2)根据蚁群算法的并行性,采用双种群群算法蚁群算法计算多目标问题,为运行人员同时提供多组较优解,增加了算法的灵活性和全局寻优能力。

[1] 胡泽春,王锡凡.配电网无功优化的分时段控制策略[J].电力系统自动化,2002,26(6)：45-49.

[2] 王秀丽,李正文,胡泽春,等.高压配电网无功/电压的日分段综合优化控制 [J].电力系统自动化,2006,30 (7)：5-29.

[3] Youman Deng,Xiaojuan Ren.A Heuristic and Algorithmic Combined Approach for Reactive Power Optimization With Time-Varying Load Demand in Distribution Systems[J]. IEEE Transaction on Power Systems,2002,17(4)：1068 -1072.

[4] 王淳,程浩忠,陈恳.配电网动态无功补偿的整体优化算法 [J].电工技术学报,2008,23(2)：109-114.

[5] 赖永生,刘明波.电力系统动态无功优化问题的快速解藕算法 [J].中国电机工程学报,2008,28(7)：32-39.

[6] Liang R H,Cheng C K.Dispatch of main transformer ULTC and capacitors in a distribution system[J].IEEE Trans on Power Delivery,2001,16(4)：625-630.

[7] 蔡昌春,丁晓群,王宽,等.动态无功优化的简化方法及实现 [J].电力系统自动化,2008,32(5)：43-46.

[8] 任晓娟,邓佑满,赵长城,等.高中压配电网动态无功优化算法的研究 [J].中国电机工程学报,2003,23(1)：31-36.

[9] 舒隽,张粒子,刘易,等.电力市场下日无功计划优化模型和算法的研究 [J].中国电机工程学报,2005,25 (13)：80-85.

[10] Hus YY,Lu F C.A combined artificial neural network-fuzzy dynamic programming approach to reactive power/voltage control in a distribution substation[J].IEEE Transaction on Power Systems.1998,13(4)：1265-1271.

[11] 缪楠林,刘明波,赵维兴.电力系统动态无功优化并行算法及其实现 [J].电工技术学报,2009,24(2)：150 -157.

[12] 刘明波,朱春明,钱康龄,等.计及控制设备动作次数约束的动态无功优化算法 [J].中国电机工程学报,2004, 24(3)：34-40.

[13] 摄伟,刘健,周艳.考虑时段优化的地区电网无功电压优化控制 [J].电力系统自动化,2009,33(4)：31-35.

[14] 张勇军,俞悦,任震,等.实时环境下动态无功优化建模研究 [J].电网技术,2004,28(12)：12-15.

[15] 方兴,郭志忠.配电网时变无功优化方法 [J].电力系统自动化,2005,29(9)：40-45.

[16] 许有方.华中电网500 kV枢纽变电站的有载调压器和静止无功补偿器 [J].电网技术,2003,27(6)：68-70.

[17] 杨斌文,刘芳.有载分接开关的质量检测、运行管理与故障处理 [J].变压器,2009,46(2)：47-49.

[18] 周鑫,诸弘安,马爱军.基于多种群蚁群算法的多目标动态无功优化研究 [J].电网技术,2012,36(7)：231 -236.

[19] 颜伟,田甜,张海兵.考虑相邻时段投切次数约束的动态无功优化启发式策略 [J].电力系统自动化,2008,32 (10)：71-75.

[20] Dorigo M,Maniezzo V,Colorni A.Ant system：optimization by a colony of cooperating agents[J].IEEE Transactions on SMC,1996,26(1)：29-41.

[21] 陈珩.电力系统稳态分析 (第二版)[M].北京：中国电力出版社,1995.

[22] 崔逊学.多目标进化算法及其应用 (第一版)[M].北京：国防工业出版社,2006.

[23] LIU Fang,C.Y.Chung,K.P.Wong.Hybrid Immune Genetic Method for Dynamic Reactive Power Optimization[J]. Power System Technology,2006.PowerCon 2006,Oct 22-26.2006：1-6.

To consider the control variables limits in a day of the dynamic reactive power optimization which load changes,according to the characteristic of the a space-time close coupled a new model for dynamic reactive power optimization is proposed,which the objective functions is minimum power loss throughout the day and the minimum switching operations,by limits of regulation time.In order to get different target groups of the better solutions,many kinds of way are used to change the pheromone.The colony optimization search strategy of ACOA is improved,they can find compensation buses that have a greater impact on network on network losses and improve the search speed.Test on IEEE 14bus、IEEE 30bus systems demonstrate the efficiency of the proposed model and algorithm. The results show that the model and algorithm can effectively control the regulation and distribution of the number of variables.

Dynamic Reactive Power Optimization;Dual-Ant Colony algorithm;Multi-objective

TM74

B

1006-7345(2014)01-0098-05

2013-12-03

周鑫 (1984),男,硕士,工程师,云南电网公司电力研究院,主要从事励磁及保护工作 (e-mail)zhouxin8421@126.com。

Dynamic Reactive Power Optimization on the Basis of Dual-Ant Colony algorithm

ZHOU Xin,LIU Zhukui,XU ShouDong

(Yunnan Electric Power Research Institute,Kunming 650217)