继电保护装置更换优化

王睿琛,薛安成

(1.云南电力调度控制中心,昆明 650011;2.华北电力大学,北京 102206)

继电保护装置更换优化

王睿琛1,薛安成2

(1.云南电力调度控制中心,昆明 650011;2.华北电力大学,北京 102206)

从可靠性经济的角度对继电保护装置的最小维修模型建模,并基于该模型计算最优更换周期。具体地,采用泊松分布拟合和Cramer-von Mises拟合优度检验确定继电保护装置的故障特性,采用对数正态分布拟合保护装置修复特性,从而构建最小维修模型;进一步,将单位生命周期费用应用于继电保护可靠性评估,制定以单位生命周期费用最小为目标的继电保护装置更换策略。依据现场保护装置实际运行数据,并考虑保护双重化的影响,求解最优更换周期,验证了该策略的可用性。

继电保护装置;最小维修;单位生命周期费用;最优更换周期

1 前言

大容量电力系统互联及大停电事故,使得继电保护装置可靠性愈发受到重视,也对保护装置的维护、检修也提出了更高要求。如何评估继电保护装置可靠性,确定其检修依据和更换策略,成为学者们关注的重要课题之一。

目前,继电保护检修周期研究已经取得了较多成果。其主要思想是基于Markov状态方程构建保护系统模型,并以稳态不可用率或年均经济损失最小为目标,从而获得最优检修间隔时间。具体地,文献 [1]提出 “潜在失效 (Hidden Failure)”概念,对保护装置的修复和检修作了初步研究。在此基础上,文 [2]建立了保护装置最简单的5状态Markov状态模型,以稳态不可用率最小为目标求解最优检修间隔时间。进一步,影响保护系统最优检修周期的各种因素如后备保护[3-4]、 微机保护自检功能[5-6]、 软件失效率[7]、被保护元件的故障情况[8]、保护双重化[9]和二次系统[10-11]等,逐一被考虑到保护装置的最优检修周期计算。此外,文献 [12]对目标函数作了改进,提出以保护年均经济损失最小为目标获得最优检修时间间隔。

理论上,依据获得的最优检修周期对保护装置进行周期定检能预防保护装置的故障,提高保护装置的可靠性。然而,上述基于状态空间转移的稳态状态概率算法需要假定每次对保护装置的检修都是有效且能使装置 “修复如新”,实际上保护装置的可靠性在使用一定时间后会下降。因此,上述假设使得结果偏于乐观。此外,实践表明,不适当的周期检修非但无效,甚至还会降低装置的可靠性。例如,不合适宜的超量检修容易引发不必要的人为故障。

因此,保护装置的可靠性和检修的经济性随着装置使用年限的增加而降低,一味地强调检修,对电网运行的经济性、可靠性和安全性造成威胁。所以,更换低可靠性或不值得维修的保护装置,从而弥补周期检修的不足,已经成为电力工业界保证装置运行有效性和维修经济性的共识。

鉴于目前针对保护装置的最优更换周期研究尚未见文献报道 (现有文献仅涉及检修周期)。本文提出一种基于现场运行数据,综合考虑保护装置可靠性和其维修经济性的最优更换策略。该策略包含两部分：依据继电保护装置可靠性构建的保护装置最小维修模型和依据该模型提出的以“单位时间生命周期费用”最小为目标函数的保护装置最优更换周期。根据现场保护装置实际运行情况形成数据,并考虑实际情况下保护双重化的影响,验证了该策略的可行性。

2 最小维修与最小维修模型

继电保护装置硬件模块具有分散集成的特点,其故障之后的维修,通常只涉及部分元件,例如对板卡、电源等的更换。此类仅仅修复、更换故障元件,不做整体更换的方式,称之为 “最小维修”。

对保护装置而言,修复后处于与故障前近似相同的状态,是一种 “修复如旧”的状态。相应地,基于最小维修方式下,对继电保护装置运行、维护特性建模,称之为保护装置的最小维修模型。

基于可靠性数学理论,最小维修数学涉及系统故障特性和修复特性两个方面。因此,继电保护装置最小维修模型的构建,如图1所示,包含装置故障特性建模和修复特性建模两个方面。具体的,对于故障特性建模,首先要进行故障时间间隔的趋势检验,其次是拟合优度检验,进而确定使用非其次泊松分布来表征故障特性;对于修复特性,首先确定合适的修复时间的概率分布函数;其次,进行模型的参数估计。

图1 构建保护装置最小维修模型

3 故障特性建模

保护装置的故障特性 (包含软件,硬件等各种故障的整体故障特性)表现为故障时间和故障次数之间的相互关系,可用故障强度函数ρ(t)表示[13]。受最小维修影响,保护装置的故障时间间隔不是独立同分布,保护装置状态可能随时间增长逐渐恶化,后继的故障时间间隔会表现出相关性或某种趋势。故将此过程看作是随机点过程,使用非齐次泊松过程[14]进行建模。

故障强度函数ρ(t)定义为故障次数对时间的导数,即

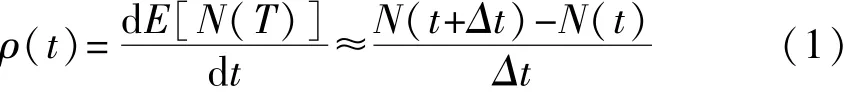
其中,N(t)为t时刻的故障次数。强度函数ρ(t)是可修复系统故障的绝对率值,ρ(t)Δt表示在Δt时间内发生故障的概率。

依据泊松公式,保护装置遵循非齐次泊松过程的强度函数可表示为

ρ(t)=abtb-1(a,b＞0) (2)

上式称为具有幂律过程的故障特性。对于故障强度函数ρ(t),若b＜1,则随时间增加保护装置状态逐渐变好,该情况可能会在保护装置投运的初期出现;若b＞1,则随时间增加变化保护装置变差,即在最小维修中装置所经历的过程。对于继电保护装置,其强度函数参数可由参数估计和概率检验获得。具体如下文所示。

此外,故障次数的期望值和瞬时平均无故障运行时间(MTBF,Mean Time Between Failure)分别为式 (3)、(4) 所示[13]

E[N(t)]≈∫0tρ(τ)dτ (3)

3.1 故障特性模型的参数估计

强度函数ρ(t)=abtb-1的参数a和b可用最大似然估计 (MLE)进行参数估算。

假设某保护装置从投运到t时间范围,n次连续的故障时刻t1＜t2＜…tn被记录,则估计值 b^、a^、ρ^分别由式 (5) ～ (7)表示

ρ^(t)=a^b^t^b-1(7)

3.2 故障特性模型检验

在估算故障强度函数的参数之后,需要进行故障特性模型检验。该检验主要包含两步,一是趋势检验,即检验故障时间间隔趋势,如果故障间隔存在趋势,故障强度函数就是合适的模型。二是拟合优度检验,即检验非齐次泊松过程 (和齐次泊松分布相比)是否适合模拟故障特性。本文采用Cramer-von Mises拟合优度的检验。

3.2.1 故障时间趋势的检验

对于强度函数ρ(t)=abtb-1,检验的假设为

H0：强度函数为常数 (b=1);

H1：强度函数不为常数 (b≠1)。

如果强度函数不是常数,说明故障时间存在趋势,不论保护装置状态存在增长或退化的趋势,均使用非齐次泊松过程来模拟。检验的统计量由下式计算：

这里,n为故障次数,检验统计量χ2为卡方(chisquare) 分布。 若当 χ2＜χ2crit,1-α/2或 χ2＞χ2crit,α/2时,则拒绝装置的故障率为常数,即接受该装置的故障强度函数不为常数。

确定装置的故障率不为常数之后,再在此基础上再进行Cramer-von Mises拟合优度的检验,以确定非齐次泊松过程是比齐次泊松分布更适合模拟故障特性的模型。

3.2.2 Cramer-von Mises拟合优度的检验

假设,

H0：用强度为abtb-1的非齐次泊松过程模拟装置的运行状态;

H1：上述过程不能模拟装置的运行状态。

首先,b的无偏估计量为

其次,Cramer-von Mises拟合优度检验统计量由下式计算：

当CM＞Cα(显著性水平α的临界值)时,拒绝原假设,即上述故障过程不可用非齐次泊松过程描述。

当CM＜Cα(显著性水平α的临界值)时,接受原假设,即上述故障过程可用非齐次泊松过程来描述。

4 修复特性建模

保护装置故障之后,需要退出运行对其进行维修。“停运时间”,一方面可以描述保护装置故障的复杂程度,另一方面也表征故障带来的损失。由于故障模式、元器件库存,以及维修人员技能水平差异等原因,停运时间具有随机特性。因此,“停运时间”是随机变量,可使用 “停运时间”的概率分布,通过拟合来构建保护装置修复特性模型。常用的分布函数的累积概率密度函数如 (11) ～(14)所示,

指数分布累积分布函数：

F(t)=1-exp(-λt) (11)

Weibull累积分布函数：

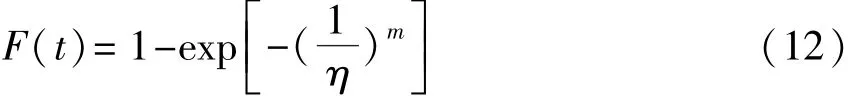
正态分布：

对数正态分布：

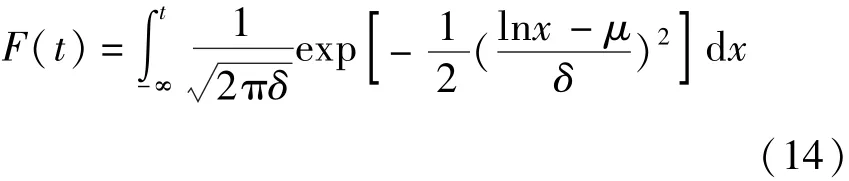
依据分布函数 (11)～(14),对停运时间采用线性回归拟合,选取拟合度最高的分布,本文引入可决系数R2来度量拟合度,可决系数表示为

yi表示离散点的纵坐标,y表示样本均值,^yi表示理论回归值。R2可以度量回归曲线的拟合程度,它在0～1之间取值,越接近1表示拟合程度越好。在维修模型中,选取拟合度最好的分布函数来模拟维修特性并进行参数估计。

进一步,平均修复时间MTTR(Mean Time to Repair)可以通过下式计算

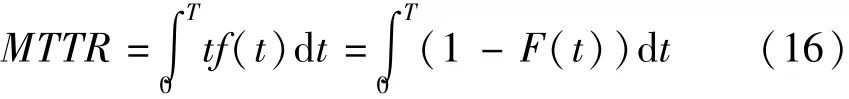
5 继电保护装置更换策略

保护装置在每次故障之后更换相应的故障元件,整个装置处于不断老化的状态。保护装置故障的持续增加,既影响其维修经济性,也降低其可靠性,故需要综合考虑经济性和可靠性,适时整体更换。下文考虑以单位生命周期费用最小为目标,综合考虑经济性和可靠性,获得保护装置最优更换周期。

保护装置从投运到t时刻,生命周期费用如下式表示,

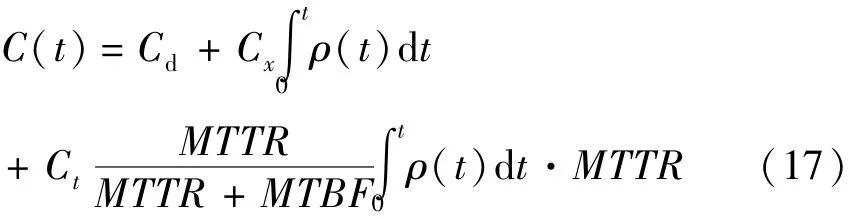
其中,

Cd——一台保护装置的单价,万元/台

Cx——每次故障后维修的平均费用,万元/次

Ct——因保护装置停运导致本线路退出运行损失的费用,万元/次·小时

考虑保护双重化配置,当两台保护装置同时停运时线路才退出运行MTTR/(MTTR+MTBF)表示另一台保护装置的不可用率,此时,线路停运,负荷失电。

因此,最小维修方式下,基于故障特性和修复特性,可获得保护装置单位时间的生命周期费用为

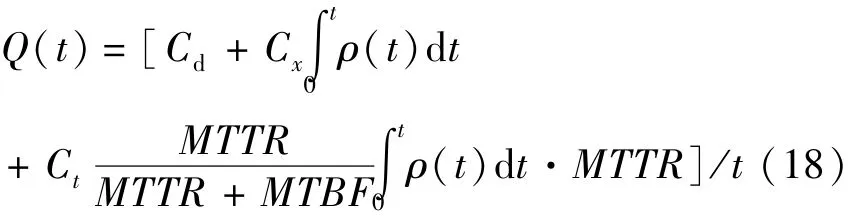
若考虑保护装置的最优更换周期满足 “单位生命周期费用”最小,则该最优更换周期满足

dQ/dt=0 (19)

进一步,根据 (19)可知,使单位时间费用最小的最优更换时间T,如下式所示。

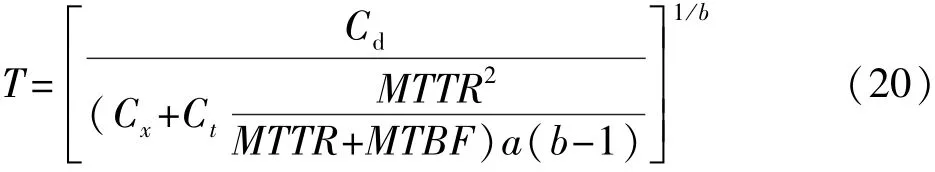
如果b≤1,则上式无解,即应当更换该套保护装置。

6 算例分析

本算例的保护装置运行和维护情况来源于变电站 “事件顺序记录系统 (SER)”及 “运行日志”,包括投运时间、故障时间和每次故障的停运时间。

该保护装置自投运起,一共运行了60000小时。其间保护装置一共故障12次,每次故障时刻(单位：小时)分别为2 234.2 13 842.5 22 752.6 33 246.8 39 416.7 46 467 49 528.4 50 852.3 56 048.1 57 240.7 58 000.1 58 432.5(小时);每次故障的停运时间 (单位：小时)为7.3 17.2 24 2.5 8 10 44.5 12 25.7 4.5 72 6.4。

6.1 故障特性建模

根据表1所示数据可得该套保护装置无故障运行时间间隔的趋势图,如图2所示。图2表明,在投入运行的7年中,该保护装置发生故障的时间间隔在缩短,故可以假设其故障时间服从幂律强度函数的非齐次泊松过程。

图2 保护装置无故障运行时间趋势图

根据 (5)、(6)式利用极大似然估计,可得^

b=1.59,^a=2.89×10-7

因^b＞1,故系统在退化。其趋势检验统计量为

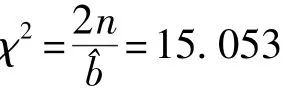
其自由度n=24。在显著性水平为10%时,卡方临界值近似为15.7和33.2。因χ2＜15.7,故拒绝幂律函数为常数 (b=1)的假设,即失效时间间隔存在下降趋势。同时,Cramer-von Mises优度检验可得CM=0.24,在显著性水平为10%时,临界值Cα为0.33,CM=0.24＜0.33,所以非齐次泊松分布可模拟装置运行状态。

6.2 修复特性建模

根据式 (11)～ (14)所示分布函数的线性回归函数,使用最小二乘法拟合停运时间,可得四种拟合的可决系数如表1所示。

表1 继电保护装置停运时间数据分布拟合优度

表1表明,正态分布可决系数最小,拟合优度最差;对数正态分布可决系数最接近1,拟合优度最好,如图3所示。因此,本文使用对数正态分布模拟保护装置的修复特性。

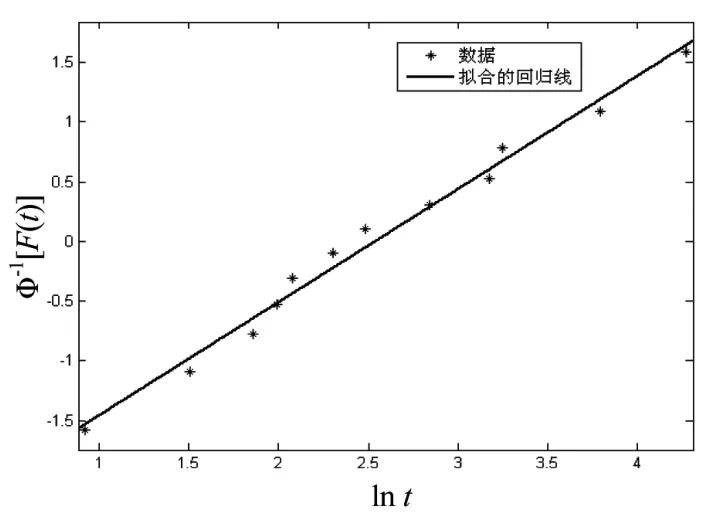
图3 停运时间数据的最小二乘拟合

极大似然估计获得对数正态分布的参数为t

^mel=12.67,s^=0.93

该分布下,平均停运时间为

MTTR=t^mel·exp(s^2/2)=19.5 h

6.3 最优更换时间

根据某公司提供数据,该保护装置售价为30万元/台,Cd=30万元。进一步,采用文献 [12]的价格数据,即Cx=0.5万元/次、Ct=10万元/次·小时,可得保护装置投运时间与单位生命周期费用关系,如图4所示。图4表明,保护装置的单位生命周期费用随使用时间的推移有先减小后增大的趋势。

进一步,根据式 (19)可得单位生命周期费用最小的保护装置最优更换周期：

T=105 680gh

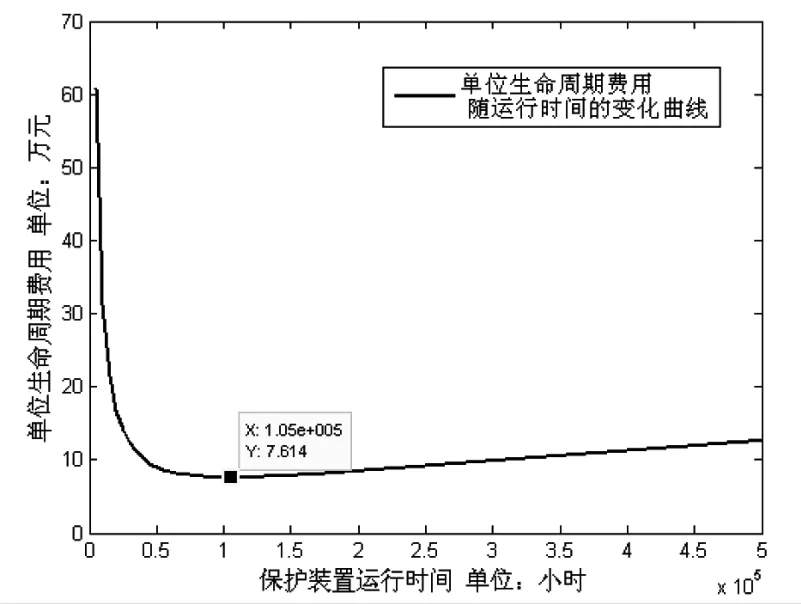
图4 单位寿命周期费用随使用时间的变化曲线

该保护装置最优更换周期约为12.07年。

据以上结果分析,该套保护装置的使用年限处于正常水平。

实际上,电力行业根据多年运行经验所获的标准规定[15],微机保护的使用年限一般不低于12年,对于运行不稳定,工作环境恶劣的装置可根据运行情况适当缩短使用年限。本文所获的更换周期与继电保护运行管理规程推荐的更换周期基本一致。

7 结束语

1)文中分析了继电保护装置的最小维修模型建模方法。对其所蕴含的故障特性和修复特性建模,采用泊松分布拟合和Cramer-von Mises拟合优度检验确定继电保护装置的故障特性;采用对数正态分布拟合保护装置修复特性。

2)提出了单位生命周期费用最小下的综合考虑保护可靠性经济的最优更换策略,并应用到最小维修模型的继电保护装置中,建立了基于最小维修模型的以单位生命周期费用最小为目标函数的保护装置最优更换周期模型。

3)基于保护装置现场运行数据的继电保护装置可靠性分析和最优更换周期结果,验证了方法的有效性。但是,由于缺乏现场保护装置运行的完整的生命周期数据,未能结合工程实际情况对该策略的有效性进行深入研究。

[1] S C Chay,M.Mazumdar.Determination of test intervals in certain repairable standby protective systems[J].IEEE Transactions on Reliability,1975,Aug：201-205.

[2] C Singh,A D Patton.Protection system reliability modeling：unreadiness probability and mean duration of undetected faults [J].IEEE Transactions on Reliability,1980,Oct：339 -340.

[3] P M Anderson,S K Agarwal.An improved model for protective -system reliability[J].IEEE Transactions on Reliability, 1992,42(3)：339-340.

[4] 孙福寿,汪雄海.一种分析继电保护系统可靠性的算法[J].电力系统自动化,2006,30(16)：32-35.

[5] Kumm J,Hou D.Predict the optimum routine test interval for protective relays[J].IEEE Transactions on Power Delivery, 1995,10(2)：659-665.

[6] 李永丽,李致中,杨维.继电保护装置可靠性及其最佳检修周期的研究 [J].中国电机工程学报,2001,21(6)：63-65.

[7] 王钢,丁茂生,李晓华,等.数字继电保护装置可靠性研究 [J].中国电机工程学报,2004,24(7)：47-52.

[8] R Billinton,M Fotuhi-Firuzabad,T.S.Sidhu.Determination of optimum routine test and self-checking intervals in protective relaying using a reliability model[J].IEEE Transactions on Power Systems,20012,17(3)：663-669.

[9] Anderson P.An improved reliability model for redundant protective system-Markov models[J].IEEE Transactions on Power Systems,1997,12(2)：573-578.

[10] A.Abbarin,M.Fotuhi-Firuzabad.Evaluation of redundancy and effect of protective components on protection system reliability[C].5th International Conference on Electrical and E-lectronics Engineering,Dec 2007,Bursa,TURKEY,ELECO2007.

[11] A Abbarin,M Fotuhi-Firuzabad.A novel routing test schedule for protective system using an extended component-based reliability model[C].International Conference on Electrical and Electronics Engineering,ELECO2009.

[12] 丁茂生,王钢,贺文.基于可靠性经济分析的继电保护最优检修周期 [J].中国电机工程学报,2007,27 (25)：44-47.

[13] 曹晋华,程侃,可靠性数学引论`[M].高等教育出版社,2006.

[14] Charles E Ebeling.可靠性与维修性工程概论 [M].清华大学出版社,2010.

[15] 继电保护装置运行管理规程.中华人民共和国电力行业标准 [S].DL/T587-2007.

近日,南瑞继保PCS系列产品通过中国电机工程学会鉴定,PCS系列产品体现了南瑞继保多年的技术积累和创新成果,基本涵盖了电网、电厂及新能源二次保护控制的核心应用。基于UAPC平台的发电机励磁系统、机组功率突降切机装置、远动装置、保护信息管理装置、SOPHIC实时监控软件平台和基于该平台的继电保护及故障信息管理系统、能源管控系统、新能源功率预测系统,全部通过了由相关行业和系统专家组成的鉴定委员会的鉴定。

此次鉴定的产品中,发电机励磁系统基于瞬时相位直测法的发电机转速快速测量技术、具有全域高阻尼特性的电力系统稳定器模型、整流元件级智能均流及故障保护技术和磁信号谐波传感器判断旋转整流二极管故障判断技术为国内外首创,发电机励磁系统整体技术达到国际领先水平。能源管控系统等其他7个产品,整体技术均处于国际先进水平,其中各产品均有多项技术属首创,达到国际领先水平。(信息来源：北极星智能电网在线)

Relay Replacement Strategy Based on the Least Unit Life-Cycle Cost with Minimum Maintenance Model

WANG Ruichen1,XUE Ancheng2,
(1.Yunnan Electric Power Dispatching and Controlling Center,Kunming 650011; 2.North China Electric Power University,Beijing 102206)

The minimum maintenance model for relay is constructed with the viewpoint of relay reliability and maintenance economy. Based on the proposed model,the optimal replacement strategy is proposed.Specifically,the Poisson distribution fitting and Cramer -von Mises goodness of fit test are used to determine the failure characteristics of protection devices;and the log-normal distribution is used to fit repair features of protection device.With the above failure and repair property,the minimum maintenance model is constructed.Furthermore,the“unit life-cycle cost”is applied in protection device reliability assessment to formulate the replacement strategy with the objective of least“unit life-cycle cost”.Finally,the optimal replacement cycle for a field operating relay is obtained with the proposed strategy,with the considering for double protection.The simulation results demonstrate valid of the proposed method.

protection device;minimum repair;unit life-cycle cost;optimal replacement cycle

TM58

B

1006-7345(2014)01-0053-06

2013-07-09

王睿琛 (1986),男,硕士,云南电力调度控制中心,从事电网调度工作。

薛安成 (1979),男,博士,副教授,华光电力大学,研究方向为电力系保护与控制。