无验潮测深系统精度分析
2014-03-16陈金湖
陈金湖
(广州南华工程管理有限公司,广东 广州 510230)
无验潮测深系统精度分析
陈金湖
(广州南华工程管理有限公司,广东 广州 510230)
三亚防波堤施工中采用无验潮测深系统对施工质量进行过程控制。根据其原理和特点,通过对仪器的系统误差、无波浪影响下测深系统的误差和在波浪影响下测深系统的误差的精度比对,测量精度满足规范要求。与传统测量模式相比,测量精度更高。
无验潮测深系统;精度比对;精度分析
无验潮测深系统是 RTK-GPS 定位技术的运用。在三亚防波堤工程施工中,引进了无验潮测深系统对施工质量进行过程控制,并承担水下工程施工质量验收工作,系统的测量精度直接影响到工程质量控制和对施工成果的评价。为确保测量精度,监理工程师对系统进行了精度比对和分析工作。
1 无验潮测深系统的原理和特点
无验潮测深系统由 RTK-GPS、测深仪、数据采集计算机组成。其原理为利用 RTK-GPS 的高精度三维定位技术和回声测深仪通过计算机同步测定水面某点的瞬时高程和水深值,推算该点的海底高程。RTK-GPS 通过与测量软件相结合,可以实现波浪补偿的功能。
相对传统的水深测量系统,无验潮测深系统最突出的特点是运用高精度 GPS 进行三维定位,无需建立临时验潮站和人工验潮,人工操作环节少,人为引起的错误和误差机率小,测量精度高。
2 无验潮测深系统精度的理论分析
2.1 仪器的系统误差
在测量过程中,构成系统的各类仪器、设备存在系统误差[1],分别表示为:测深仪的 系统误差ΔSi;GPS 的系统误差 ΔHi;连接 GPS 与测深仪换能器连杆的长度测量误差 ΔLi。
2.2 无波浪影响下测深系统的误差
在无波浪影响的情况下,海底面某点高程的瞬时测量值可表示为:
H=HGPS+L+S (1)
式中:HGPS为 GPS 测定的海面某点瞬时高程测量值;L为连杆长度的测量值;S为测深仪测定的海面某点瞬时水深值。
考虑测量过程中的仪器误差,对仪器引起的误差进行了修正,则有海底面某点高程的真值H0为:
H0=(HGPS+ ΔHi)+(L+ ΔLi)+(S+ ΔSi)=
H+(ΔHi+ ΔLi+ ΔSi)=H+ Δ (2)
也就是测深系统的误差为 Δ:Δ = ΔHi+ ΔLi+ΔSi。
可以看出,在无波浪影响的情况下,无验潮测深系统的测量精度取决于构成系统的仪器精度。同时,由于 RTK-GPS 的三维测量精度达到厘米级,本工程所用仪器的垂直精度为 3 cm+2 × 10-6× D,D 为测量距离,km;测深仪的测量精度为±( 0.4%+ 5 cm);连杆的测量精度用钢卷尺量可以达到毫米级,对于一个固定测区,ΔHi和 ΔLi是固定的,且其误差值相对于测深值可以忽略不计,故影响测量系统的误差取决于测深仪的测量精度,而经过校准后的测深仪精度可以满足规范的要求。
2.3 在波浪影响下测深系统的误差
在波浪影响下,测量系统将随着测量船一起发生左右、前后和上下的摇动,测量系统除固定的仪器误差外,将不可避免的发生由于摇动引起的误差,其误差发生过程是复杂的综合运动,分析如下:
1)各种仪器系统误差同样存在。
2)当系统在风浪条件下产生摇摆,瞬时测量中心轴线将以轴线上某一点A为圆心发生倾斜并与原轴线方向形成一夹角α,同时整个系统随着波浪发生上下位移,对系统的运动引起的误差进行分析,难度较大,但其运动对平面定位的影响不会超出规范允许范围,其在垂直方向的运动将对测深精度有比较大的影响,为方便分析,将系统的综合运动简化为A点的垂直运动和测量中心轴线以A点为中心旋转运动。
设波浪作用时,A 点高程变化量为 ΔD,测量中心轴线以A点为中心旋转一夹角α。分析测量过程,A点高程变化量ΔD将在测量过程由测深部分消除,故不考虑其影响。结合瞬时其他误差,从式 (2) 可以推导出式 (3):

则此时系统的误差为 Δ′:

从上面分析,系统在波浪作用下存在两项误差,其中 (ΔHi+ ΔLicos α + ΔSicos α) 主要是仪器误差引起,可以通过严格校准工作得到控制。对于[( L+S )( 1-cos α )]来说,该项主要是波浪作用下纵横摇摆发生角度α的倾斜引起的,在本工程中最大水深大于 30m,(L+S)的值近 40m,其引起的误差是不可忽视的;另外,(1-cosα)的值将随α的加大而明显增大,在某一瞬时,[( L+S )( 1-cos α)]的值随 α 的加大而增大且恒为正值,如图 1(图中设 L+S=40m),故 [(L+S)(1-cosα)]的值恒为正值,是影响系统精度的关键误差项目;而对于不同的时刻,即不同瞬时点,S 及 α 为无规律变化值,故 [(L+S)(1-cosα)]的值呈无规律变化,无法通过合理的方法克服,也无法确定合理的修正值。

图1 α 与[(L+S)(1-cosα)]关系图Fig.1 Relation between α and[( L+S )(1-cos α)]
综上所述,在波浪影响下作业,系统将存在不可忽略的误差,测量精度将下降,其误差为瞬时综合误差,随机出现,无规律,无法采用合理的方法消除。
3 无验潮测深系统的精度验证
通过理论分析,只得出定性的结论,未有定量的结果。鉴于防波堤垫层石的厚度仅为 1.5m左右,且对坡面质量要求高,从质量控制的角度出发,应对该系统在波浪影响下的测深精度进行验证,并通过试验统计分析找出该系统在风浪工况下的使用范围,以保证工程质量。
3.1 比对试验方案设计
比对试验区水深大于 30m,采用 SDH-13D回声测深仪( 精度 0.4%+5 cm )及 HD-5200 型RTK-GPS( 精度 3 cm+2 × 10-6× D)进行比对。
1) 试验项目。实时相位差分定位系统(RTK-GPS)的三维定位稳定性试验;测深仪的测深精度和稳定性;无验潮测深法在波浪条件下的测深精度。
2) 平面和高程控制。平面控制采用任意坐标系,高程控制采用当地理论深度基准面。采用业主提供的经承包人校核合格的控制点资料。GPS参数、坐标转换关系采用承包人的现用资料。
3) GPS 稳定性试验。在施工区附近已知高级控制点架设 GPS 接收机,连续观测 2 h 以上,从外业采集的数据分析GPS在本工程施工环境中的三维定位精度和稳定性。
4)测深仪的测深精度和稳定性试验。采用检查板比对法。测定 0~30m 范围内仪器差值,分析仪器的精度和稳定性。在海面较平静时,结合潮位预报,于高平潮或低平潮时段在拟定试验区域附近对测深仪进行测定。
5)验潮。设立临时验潮站进行潮位观测。比对试验区附近埋设工作点,按四等水准精度从高级水准点引测工作点高程。按图根水准精度测设水尺。水尺的设立按规范规定进行。验潮每 10min观测1次,内业整理采用绘制水位曲线图修正读数误差。
6) 无验潮测深法在波浪条件下的测深精度。考虑波浪条件下横摇、纵摇情况,测深按规范有关要求进行。
在施工区附近选择较平坦区域,采用定点同步比对,即测量船系在浮鼓上,处于相对自由状态,同时采用传统测量法和无验潮测量法进行测量。传统测量方法测出该点一系列海床面标高,进行相关校正后作为该点“参考真值”。
计算机同步读取无验潮测深法的一系列海床面高程瞬时值,与测量参考真值比较,得出瞬时测深误差。尽可能在此基础上进行扩大测量船两摇幅度的测深精度的理论分析,确定无验潮测深法在工程的适用范围。
3.2 比对成果和分析
3.2.1 比对试验成果
比对试验在 GPS 稳定性及测深仪比对合格的前提下进行,历时约1 h,试验同步采集测深仪的深度读数、GPS 的平面位置及水面高程读数和瞬时潮位,共采集数据 3 023 组,其中有效数据2 988 组,数据有效率为 98.8%。所有数据分布在以数据平面位置中心为圆心、半径 3.9m 的范围内,半径为 2.0m 内的数据占 78.8%,具体分布情况见表1。
根据设计图纸,该区海床面呈 1 ∶50 的自然坡度,平坦无局部隆起,则数据分布圆内海床面的高差小于 0.2m,满足规范对“图上 1mm 范围内水深点深度比对互差 ≤ 0.02H( 0.52m )”的要求,可以认为全部数据代表同一测点。

表1 数据分布半径比例Table1 Proportion of data distribution radius
3.2.2 参考真值
比对前,先采用加大加重的检查板对测深仪的测量精度进行比对调试,确保测深精度,在采集数据的同时在临时验潮站进行人工验潮,通过绘制潮位曲线,减小人工验潮读数误差,内业对采集的水深值进行有关改正后,结合潮位推算每组瞬时测点的海床面高程 Hi。设分布在数据中心点的周围的机率相等,受波浪影响的情况机率相同,则取 Hi平均值为该点海床面高程,此时可以消除海面波浪引起的水面高程误差和海床面自然坡降引起的误差;但与无验潮一样,测深同样存在摇摆引起的误差:Δ = (L+S)(1-cosα)-( ΔHi+ ΔLicos α + ΔSicos α )。
应该说,通过以上措施后,误差可简化为Δ= S( 1-cos α ),H 为 Hi的平 均值( H=25.96m ),如图 2 所示,设该海床面高程真值为 H0,则有 H0= H-Δ,故把平均值当海床面高程只是基本接近真值,其误差在规范允许的范围内,在一定程度上可以用来检验无验潮测深系统的测量精度。经过处理后,该点高程真值为 H0=25.96-Δ,Δ 值的变化规律难以确定,但恒有 H0<25.96,取 25.96 为参考真值,以检验无验潮测深系统的测量精度。
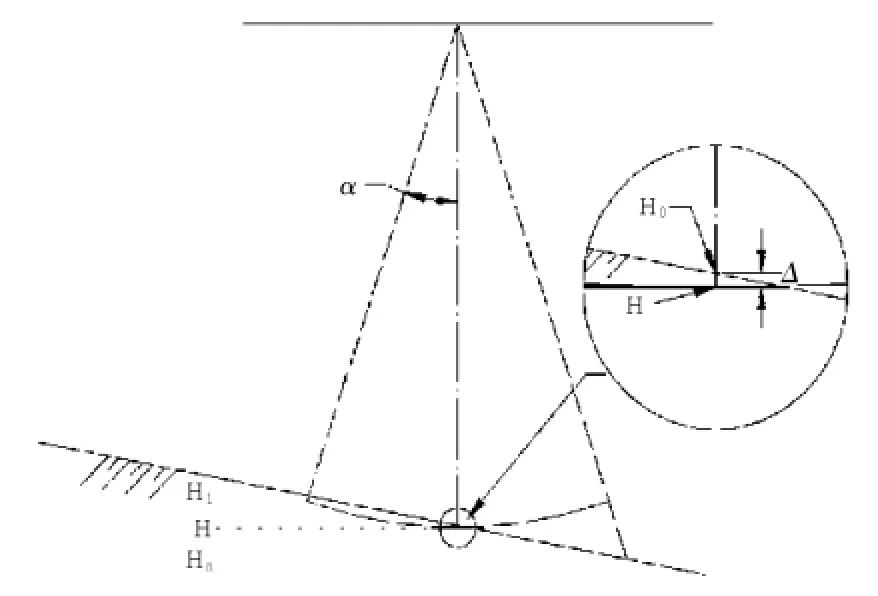
图2 高程真值与误差的关系Fig.2 Relation between the true valueand error of elevation
3.2.3 波浪分析
比对前,先在控制点上对 RTK-GPS 进行比对,确保水面高程的测量精度,对采集的数据运用 Excel电子表格的图表功能绘制波浪分析图(如图 3),分析各种波高的出现比例,经统计分析,在比对试验过程中,测区波浪情况如表 2 所示[2]。从波浪分析表可见,本次比对有 92.3%为波高0.6m 以下范围,波高 0.6m 以上仅为 8%左右,且其出现的比例很小,故本次比对只能代表无验潮测深系统在波高0.6m 以下的精度情况。
3.2.4 无验潮测深系统的比对结果分析

图3 波浪分析图Fig.3 W ave analysis diagram
采用由无验潮测深系统逐点测量值与参考真值作比较,即 Δ =H无-25.96,得出 2 988 个误差值,对其进行统计分析,误差值分布如表3所示,可以看出,96%的测点误差在规范规定的允许限差 0.02 H( 0.52m )之内,且误差在 0.3m 以内占74.6%,分析可以认为无验潮测深系统在 0.6m 波高的情况下,测量精度满足规范要求。

表2 波浪分析表Tab le2 W aveanalysis table

表3 测深误差统计表Tab le 3 Statistical table of sounding error
同时,还可以分析出无验潮测深系统测量值存在的另一情况,在 2 988 个测点中,存在 2 142个测点的值小于测量真值,即 Δ =H无-25.96<0,其比例为 72%,符合理论分析的结果,所以,无验潮测深系统测量精度满足规范要求,与传统测量模式比,其测量精度更高。
4 结语
通过简化模型和实证比对的方法对无验潮测深系统精度进行了分析,结果表明在 0.6m 波浪条件下,此系统具有较高的精度,能满足相关规范的要求。由于分析模型和比对方案设计存在一定的局限性,比对分析结果不能作为此系统在其他波高条件下测量精度的依据,故其精度和使用范围还有待于进一步的分析研究,以指导施工和推广。
[1] 卢军民,安延云,张东明,等.无验潮测深技术中影响水深测量精度的几个问题探讨[J].水运工程,2010(5):50-54. LU Jun-min,ANYan-yun,ZHANGDong-ming,etal.Some issues affecting the accuracy of non-tide sounding servey[J].Port&Waterway Engineering,2010(5):50-54.
[2] 胡志渠,李雁.RTK 无验潮测量技术用于港口水深测量[J].港工技术,2006(4):57-58. HU Zhi-qu ,LI Yan.Application of RTK surveying technique without tidal observation to depth sounding of port[J].Port Engineering Technology,2006(4):57-58.
[3] 张发栋,虞祖培.GPS 无验潮测深技术在水深测量中的应用[J].港工技术,2004(6):54-55. ZHANGFa-dong,YU Zu-pei.Application ofGPSno-tide sounding technique in sounding surveys[J].Port Engineering Technology,2004(6):54-55.
Accuracy analysis on the non tidal sounding system
CHEN Jin-hu
(Guangzhou Nanhua ProjectManagementCo.,Ltd.,Guangzhou,Guangdong510230,China)
No tide sounding system isused for the process control of construction quality in Sanyabreakwater construction.According to its princip lesand characteristics,through the precision comparison of the instrument system error,sounding system errorby nowavesaffectandmeasurementerror in thewaves influence,theaccuracy of the system canmeet regulatory requirements.Compared with the traditionalmeasurementmode,this system ishighermeasuring accuracy.
no tide sounding system; precision comparison; accuracy analysis
U652.62
A
2095-7874(2014)06-0069-04
10.7640/zggw js201406021
2014-02-17
2014-03-27
陈金湖 (1973 — ),男,广东澄海人,高级工程师,主要从事港口监理工作。E-mail:654829524@qq.com
