基于WEBENCH的巴特沃斯低通滤波器的设计

徐志国，杨 娟

(金陵科技学院电子信息工程学院，江苏 南京 211169)

几乎在所有模拟电子电路中都能看到有源滤波器，它们无处不在。音频系统使用滤波器进行频带限制和平衡，通信系统中采用滤波器调谐特定频率并消除其它频率，在数据采集系统有抗混叠滤波器，抗混叠滤波器实际上是一种低通滤波器[1]。常用的滤波器频率响应类型有巴特沃斯(Butterworth)、贝塞尔(Bessel)、契比雪夫(Chebychev)3种[2]，巴特沃斯(Butterworth)滤波器是一种具有最大平坦幅度响应的低通滤波器，它在通信领域里已有广泛应用[3]。与其它两种滤波器相比，巴特沃斯低通滤波器由于在衰减特性、相位特性和响应特性等方面具有特性均衡的优点，因此在实际使用中，巴特沃斯滤波器受到广泛使用[3]。

WEBENCH是TI公司的一款软件，它为滤波器的设计提供了最大的方便性和灵活性，可以快速地进行低通、高通、带通或者带阻滤波器的设计。WEBENCH在生成有源滤波器时，输入想要得到的滤波器的参数，TI的WEBENCH就会帮助寻找到正确的TI运算放大器，对外围电路中繁多的R、C值做出正确的选择，WEBENCH允许深度调节各种滤波器变量，优化滤波器，并具有SPICE模拟仿真功能。

1 Butterworth低通滤波器的特性

巴特沃斯滤波电路又叫最平幅度滤波电路，该滤波电路的特点是：在小于ωc(截止频率)的范围内，幅频响应具有最平幅度；在ω>ωc后，幅频响应曲线下降较快[4]。对于低通滤波电路来说，3 dB截止角频率ωc=ωH=ωn。

巴特沃斯低通滤波器的幅频特性为

(1)

写成

(2)

其中Auo为通带内的电压放大倍数，ωC为截止角频率，n称为滤波器的阶。从(2)式中可知，当ω=0时，(2)式有最大值1；ω=ωC时，(2)式等于0.707，即Au衰减了n=23 dB；n取得越大，随着ω的增加，滤波器n=8的输出电压衰减越快，滤波器的幅频特性越接近于理想特性。

当ω>>ωC时，

(3)

两边取对数，得

(4)

此时阻带衰减速率为：-20 ndB/十倍频或-6 ndB/倍频，该式称为衰减估算式。表1列出了归一化的、n为1～8阶的巴特沃斯低通滤波器传递函数的分母多项式。

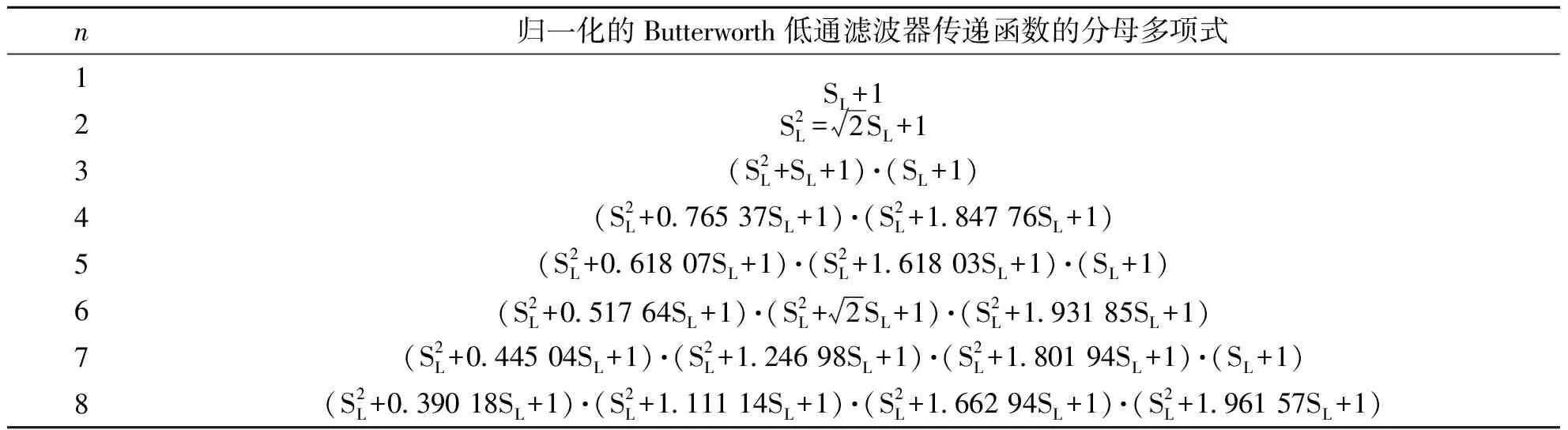
表1 归一化的滤波器传递函数的分母多项式

在表1的归一化巴特沃斯低通滤波器传递函数的分母多项式中，SL=S/ωC，ωC是低通滤波器的截止频率[5]。

(5)

(6)

(7)

(8)

2 Butterworth低通滤波器电路设计

巴特沃斯低通滤波器一般的设计步骤是先根据滤波器的指标要求确定滤波器的阶数n，然后选择具体的电路形式，再选择电路的运算放大器和算出电路中各元件的具体数值，最后完成电路安装和调试，满足指标要求。常用的有源二阶滤波电路有两种电路形式：无限增益多路负反馈二阶滤波电路和压控电压源二阶滤波电路[6]。压控电压源二阶滤波电路的特点是：滤波器是同相滤波器，其优点是拥有高输入阻抗，很低的输出阻抗，滤波器类似于一个电压源[7]。其优点是：电路性能稳定，增益容易调节。

设计一个有源低通滤波器，要求：fC=1 kHz，Auo=2，在f=10fc时，要求幅度衰减大于30 dB[8]。由衰减估算式：-20 ndB/十倍频，算出n=2。选择的低通滤波电路如图1所示。

图1 压控电压源二阶低通滤波器电路Fig.1 The circuit of two-order low-pass filter with voltage-controlled voltage source

(9)

滤波器的截止角频率

(10)

(11)

在上面几个式子中共有多个未知数，3个已知量，因此有许多元件组可满足给定特性的要求，这就需要先确定某些元件的值，再去确定其他元件的取值[9-12]。

3 基于WEBENCH的Butterworth低通滤波器设计

如何在众多的运算放大器中选择合适的一个并且计算外围元件参数来完成巴特沃斯低通滤波器的设计对一般的设计者也是个挑战，现在有了WEBENCH的帮助，只需输入想要得到的滤波器的参数，WEBENCH的滤波器设计环境就会帮助做出正确的选择，并计算出外围电路中的R、C的值。WEBENCH在生成有源滤波器时，可以调节各种滤波器变量来实现滤波器的优化。在如图2所示的窗口输入滤波器参数，截止频率fc=1 000 Hz，滤波器增益Auo=2 ，阻带频率fs=10 kHz，幅度衰减大于30 dB。

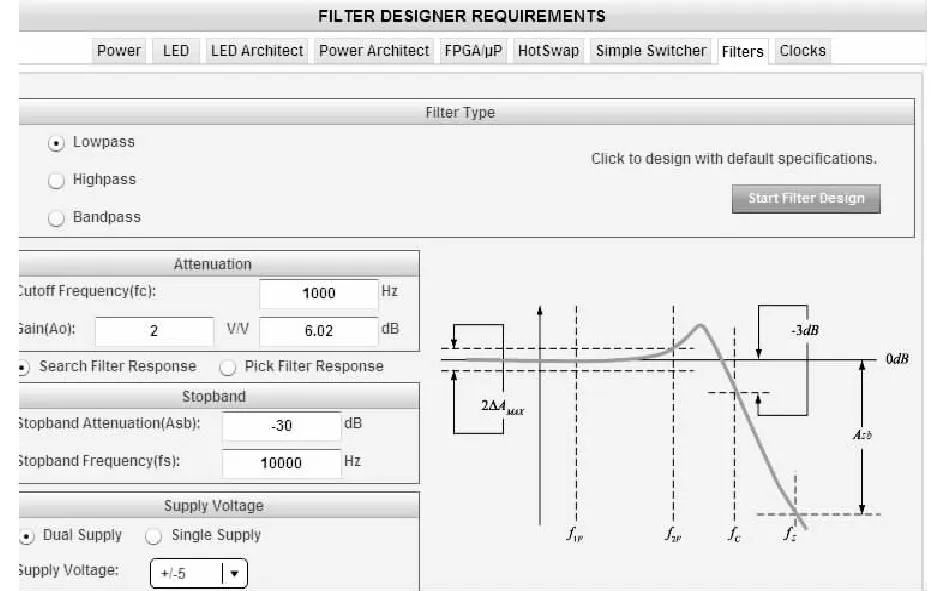
图2 WEBENCH滤波器设计参数设置Fig.2 The parameter setting of WEBENCH filter

图3是WEBENCH滤波器的设计界面，界面主要有设计优化选择、设计条件修改、方案筛选、方案的可视化对比、待选方案、方案性能曲线对比等部分组成。如图3所示，WEBENCH提供了7种方案待选，表格提供各种方案的性能参数，设计界面右下角是方案性能曲线对比，本例低通滤波器设计的频率响应类型选择Butterworth，软件计算出需要二阶滤波器[8]。

图3 WEBENCH滤波器设计界面Fig.3 The interface of WEBENCH filter

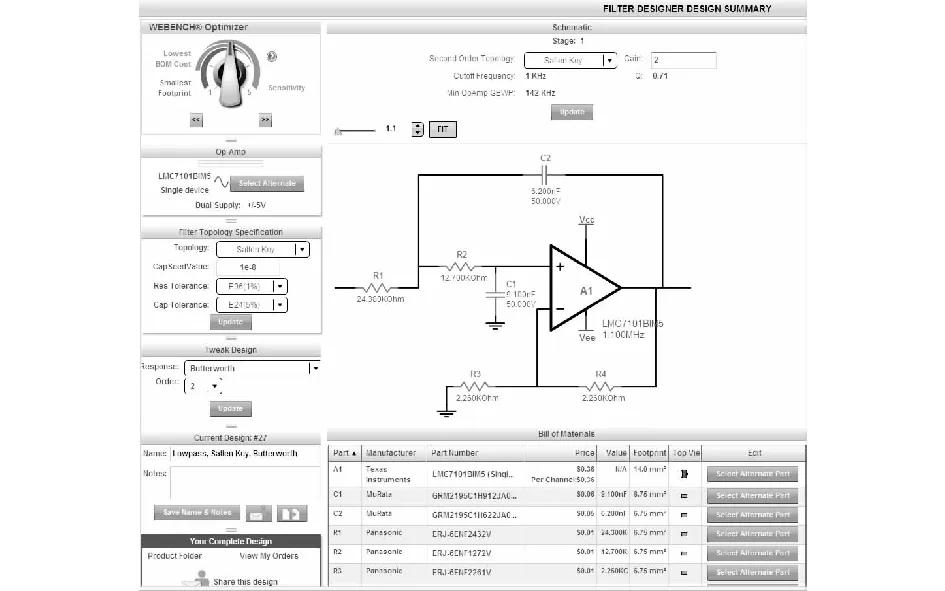
图4 WEBENCH滤波器设计仿真界面Fig.4 The simulation interface of WEBENCH filter

图4是进入仿真界面，可以看到由软件系统生成的二阶巴特沃斯低通滤波器原理图，下拉菜单项有正弦波仿真、阶跃仿真和闭环频率响应仿真项选择。原理图下方给出构成滤波器的元件大小、价格、封装等参数，并可根据需要选择其他元件。本例由WEBENCH自动选择运算放大器的型号为:LMC7101BIM5，R1=24.3 kΩ,R2=12.7 kΩ,R3=R4=2.26 kΩ,C1=9.1 nf,C2=6.2 nf。可以看出利用WEBENCH软件可以省却繁琐的运算放大器型号的选择和R、C的参数计算，便于快速地完成Butterworth低通滤波器的设计。

4 Butterworth低通滤波器仿真分析

为了验证本文设计的Butterworth低通滤波器的性能，运行仿真界面选择项的闭环频率响应，得到闭环频率响应曲线如图5所示，可以清楚地看到滤波器的-3 dB的截止频率为1 kHz，10 kHz以外的抑制在-30 dB以下，满足设计的要求。滤波器的阶跃响应如图6所示，可以看到滤波器的过冲，根据过冲的大小判断其稳定性。仿真结果表明，利用WEBENCH可以通过TI提供的运算放大器和无源组件创建出经过优化的Butterworth低通滤波器的设计。

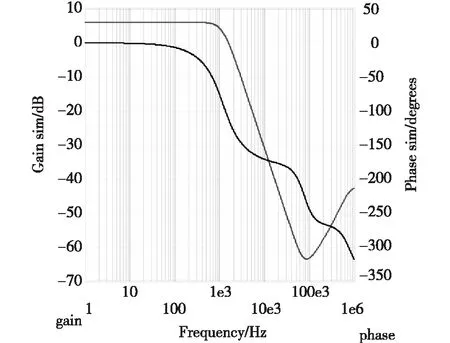
图5 闭环频率响应Fig.5 The frequency response of closed loop

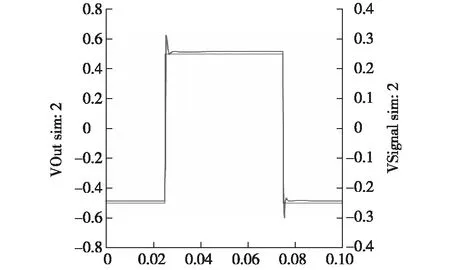
图6 阶跃响应Fig.6 Step response

5 结 语

本文在对Butterworth低通滤波器的特性进行了理论分析的基础上，根据给定的指标，采用Butterworth归一化低通原型的滤波器确定二阶Butterworth有源低通滤波器的电路设计。通过TI的WEBENCH滤波器设计器对低通滤波器进行了仿真，确定了Butterworth低通滤波器的运算放大器和外围元件参数。通过分析滤波器闭环频率响应曲线和阶跃响应曲线，验证了设计方案的正确性。研究表明利用TI的WEBENCH滤波器设计器软件，可以快速高效地设计出低通、高通、带通或带阻滤波器，方法对实际滤波器的设计具有一定的参考价值。

[1] 宋军,赵明忠.一种分析和设计抗混叠滤波器的方法[J].现代电子技术,2008(19):67-68，71

[2] 彭宏丽.基于FilterLab软件的低通滤波器的设计[J].科技情报开发与经济,2011(09):201-202

[3] 吴文婷.基于ANSOFT DESIGNER的低通巴特沃思滤波器的设计与优化[J].重庆工学院学报：自然科学版,2007(08):59-61

[4] 罗珊,孙峥,蒋新胜,等.模拟有源滤波器MAX275的原理及应用[J].国外电子元器件,2005(01):73-74

[5] 李彦哲,关恩明,张显民.巴特沃兹有源低通滤波器设计[J].黑龙江科技信息,2010,27:15

[6] 谭家杰,游开明,唐建锋,等.基于EWB高阶有源滤波器设计研究[J].衡阳师范学院学报,2007(03):55-58

[7] 丁筱玲,刘敏,李洁,等.交流发电机性能测试系统抗干扰电路的设计[J].实验室科学,2010(04):48-51

[8] 林祥金,张志利,朱智.Butterworth有源抗混叠滤波器设计[J].电子测量技术,2008(02):66-69,72

[9] 李钟慎.高阶Butterworth低通滤波电路的快速设计[J].工业仪表与自动化装置,2007(04):27-29,35

[10] 林开司,张露,林开武.巴特沃斯低通滤波器优化设计与仿真研究[J].重庆工商大学学报:自然科学版,2014(06):58-62

[11] 龚作豪,沈君凤.巴特沃斯低通滤波器的仿真设计[J].信息通信,2014(07):40-41

[12] 姜峰.数字功率均衡放大器的设计[J].金陵科技学院学报,2010(04):17-22