矩阵乘积加权广义逆几个等式的推广

万文婷

(荆楚理工学院数理学院，湖北 荆门 448000)

矩阵的广义逆在数值分析、概率统计、现代控制理论、网络理论、信息安全、测绘学等方面都有着很重要的应用，是矩阵理论的重要研究内容。关于普通的矩阵广义逆的研究由来已久且趋于成熟，近年来，作为其推广形式的加权广义逆成了矩阵理论研究的热点。文献[1-5]研究了加权广义逆的结构形式、性质、解法及应用等各类问题。而本文以矩阵的秩为工具，结合矩阵的加权广义逆存在时的相关结论，讨论了加权广义逆矩阵的性质中关于矩阵乘积的加权广义逆的表达式，从而改进和推广了文献[3-4]中一些已有的结果，这项工作在优化问题的加权信赖方法中有着极为重要的现实应用。

用Cm×n表示复数域C上m×n复矩阵集合，AH和r(A)分别表示矩阵A的共轭转置和秩，I表示单位矩阵。

1 基本概念及相关引理

定义1[4]设矩阵A∈Cm×n，M,N分别为m,n阶可逆矩阵，若存在矩阵X满足下列4个等式:

AXA=A,XAX=X, (MAX)H=MAX, (NXA)H=NXA,

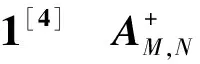
r(AHMHA)=r(AN-1AH)=r(A)。

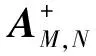
其中(AN-1AH)(1)及(AHMHA)(1)均可任取(A(1)指满足等式AA(1)A=A的广义逆[1])。

引理3[5]AB(AB)(1)A=A的充要条件为r(AB)=r(A)，

B(AB)(1)AB=B的充要条件为r(AB)=r(B)。

引理4[6]设A,B,C分别为m×n，n×s，s×m矩阵，

1) 若r(CA)=r(A)，则r(CAB)=r(AB)，

2) 若r(BC)=r(B)，则r(ABC)=r(AB)。

2 主要结果

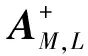
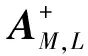
(AB)HMHAB=BHAHMHAB，ABN-1(AB)H=ABN-1BHAH均为Hermitian。

又由r(AHMHA)=r(A)及定理条件，据引理4知r(AHMHAB)=r(AB)=r(AH)，

再由引理4，有r(BHAHMHAB)=r(BHAH)=r(AB)，

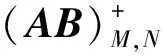
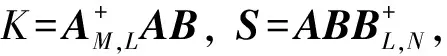
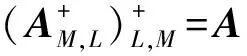
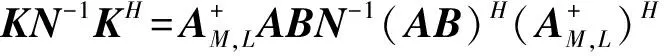
又r(AB)=r(AK)r(K)r(AB)，故r(K)=r(AB)。

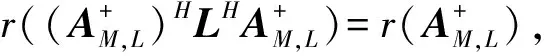
而r(AB)=r(ABN-1(AB)H)=r(AKN-1KHAH)r(KN-1KH)r(K)r(AB)，

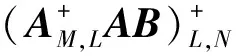
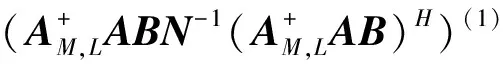
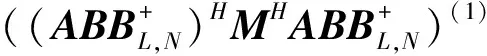
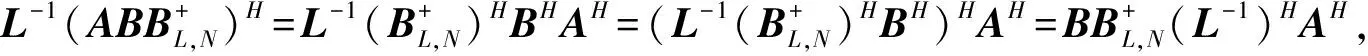
据引理2，有

由引理3，得

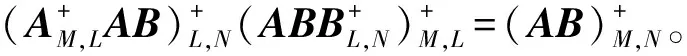
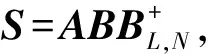
接下来，类似于定理1中(1)的证明，在证明过程中只需取

证明 令定理1中L=I即得1)、2)。

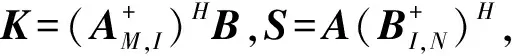
r(AB)=r(ABN-1(AB)H)=r(AAHKN-1KHAAH)r(KN-1KH)r(K)=

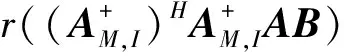
BHB((AB)HMHAB)(1)BHB，据引理2，有

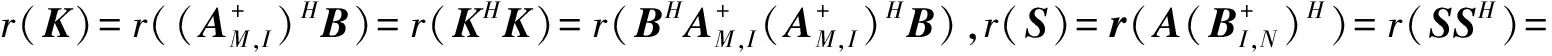
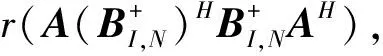
由引理3得

因此得

定理3设A∈Cm×l，B∈Cl×p，C∈Cp×n，M，N，L，P分别为m阶，n阶，l阶及p阶可逆阵。

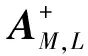
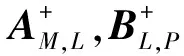
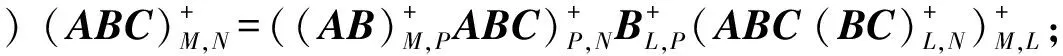
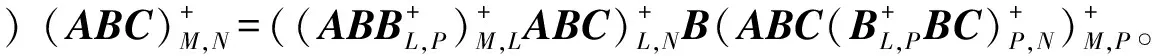
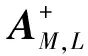
由定理条件知r(A)=r(ABC)r(AB)r(A),故r(AB)=r(A)=r(B)，同理r(BC)=r(B)=r(C)。

1)、2)的证明方法与定理1中1)的证明方法类似。 在证明过程中，只需取

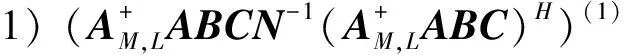
证明 令定理3中L=I，P=I即得1)、2)、3)。

而4)、5)、6)可仿照定理1和定理2中的相关证明直接进行验证。

注: 定理2和定理4推广了文献[4]中的一些已有的结果。

3 结 语

本文在权矩阵M，N为可逆矩阵的条件下，讨论了关于矩阵乘积的加权广义逆的一些恒等式。 由于矩阵乘积的加权广义逆在求解奇异线性方程的加权最小二乘问题和奇异矩阵的加权扰动分析中有着广泛的应用，因此，本文所得的结果将有助于上述各类问题的探讨与研究。

[1] 陈永林.广义逆矩阵的理论与方法[M].南京:南京师范大学出版社,2005

[2] 刘晓冀.矩阵的加权Moore-Penrose逆[J].数学物理学报,2006,26A(7):993-998

[3] Tian Yongge, Cheng Shizhen. Some Identities for Moore-Penrose Inverses of Matrix Products[J]. Linear and Multilinear Algebra, 2004,52(6):405-420

[4] 袁玩贵,廖祖华,邵益新.权为可逆阵的加权广义逆矩阵的几个恒等式[J].南京师大学报：自然科学版,2010,9(3):22-25

[5] AdiBen-Israel, Thomas N.E Greville. Generalized Inverses: Theory and Applications[M]. 2nd ed. New York: Springer-Verlag, 2003

[6] 樊恽,钱吉林等.代数学辞典[M].武汉:华中师范大学出版社,1994