基于纤维梁单元的薄壁圆钢管再生混合柱受压承载力随机分析*

赵新宇 吴波† 杨勇，2

(1.华南理工大学亚热带建筑科学国家重点实验室，广东广州510640; 2.西安建筑科技大学土木工程学院，陕西西安710055)

科学高效地回收利用建筑领域产生的大量废弃混凝土，对于促进建筑业可持续发展、实现节能减排战略目标具有重要意义.目前，国内外对废弃混凝土回收利用的研究主要集中在再生骨料混凝土领域［1-4］.有别于此，文献［5］中提出了钢管再生混合构件的概念，将废弃混凝土的回收利用从骨料层次提升到了大尺度块体或节段层次;文献［6-7］报道了中厚壁和薄壁圆钢管再生混合短柱的轴压试验结果;文献［8］对薄壁圆钢管再生混合中长柱的轴压和偏压受力行为进行了试验研究;文献［9］介绍了圆钢管再生混合柱的工程应用实例.总体上看，在钢管内填筑较大尺度的块体型或节段型废弃混凝土并与现浇混凝土混合形成的钢管再生混合柱，不仅具有与全现浇钢管混凝土柱相似的力学性能，同时还大大简化了废弃混凝土的循环利用过程.

建立准确高效的数值计算模型是研究和预测薄壁圆钢管再生混合柱非线性力学性能的重要环节.目前，钢-混凝土组合结构的数值计算模型主要有3种［10-11］:三维实体单元模型、集中塑性单元模型和纤维梁单元模型.对于薄壁圆钢管再生混合柱而言，由于其柱内废弃混凝土的几何形状不规则、空间分布不均匀、新旧混凝土的力学性能存在差异、新旧混凝土界面力学行为尚未明确等原因，建立与实际完全一致的薄壁圆钢管再生混合柱三维实体单元模型仍存在较大困难，需引入一定的假设对其进行简化处理.集中塑性单元模型构成相对简单、计算效率较高，但其引入了较多假定，计算时难以追踪构件在加载过程中塑性区域的时变情况，且其仍未能较好地解决轴力与弯矩的相互耦合问题［12］，因此本研究也不予采用.

纤维梁单元模型是一种可反映杆系结构分布塑性的梁柱单元模型［10-14］.纤维梁单元的基本假定为截面上每根纤维处于单向受力状态，基于平截面假定和单轴材料应力-应变关系，对各纵向纤维(包括混凝土纤维和钢材纤维等)进行数值积分即可求得整个截面的轴力和弯矩，因此纤维梁单元可以考虑构件轴力与弯矩的非线性耦合效应，也能够反映构件的塑性长度变化问题.纤维梁单元模型近年来受到了高度关注［15-17］，在结构随机分析领域也得到了一定的应用.Lee等［18］使用传统的(即确定性的)刚度法纤维梁单元模型，并结合中心点法建立了随机纤维梁单元计算模型，然后运用Monte Carlo方法对混凝土框架构件和结构进行了承载力随机分析;李杰等［19］在混凝土随机力学的研究框架下，根据概率密度演化方程，结合位移控制的纤维梁单元程序ZeusNL，发展了混凝土框架结构体系可靠度分析方法.

考虑到纤维梁单元具有较高的计算效率和精度，文中选择其作为计算工具，对薄壁圆钢管再生混合柱的受压承载力进行数值计算分析.首先，基于纤维梁单元的计算框架，在积分点截面引入随机生成和投放废弃混凝土块体的技术，建议了薄壁圆钢管再生混合柱受压承载力的一种随机数值分析方法，并对该方法的有效性进行验证;然后，运用该方法考察了柱子长径比、钢管壁厚、废弃混凝土取代率，以及新、旧混凝土强度差等参数对薄壁圆钢管再生混合柱受压承载力的影响.

1 计算模型

1.1 纤维梁单元模型

根据插值方式不同，纤维梁单元可分为刚度法、柔度法和混合法模型［20］.柔度法模型沿杆长对截面力进行插值，具有单根构件所需单元数量较少、能较好模拟构件弱化段等优点.经比较，文中选用柔度法纤维梁单元模型对薄壁圆钢管再生混合柱进行计算模拟.柔度法纤维梁单元的有限元列式及非线性迭代求解过程详见文献［21］，文中不再赘述.

薄壁圆钢管再生混合柱内新、旧混凝土纤维的受压应力-应变关系采用韩林海［22］提出的模型:

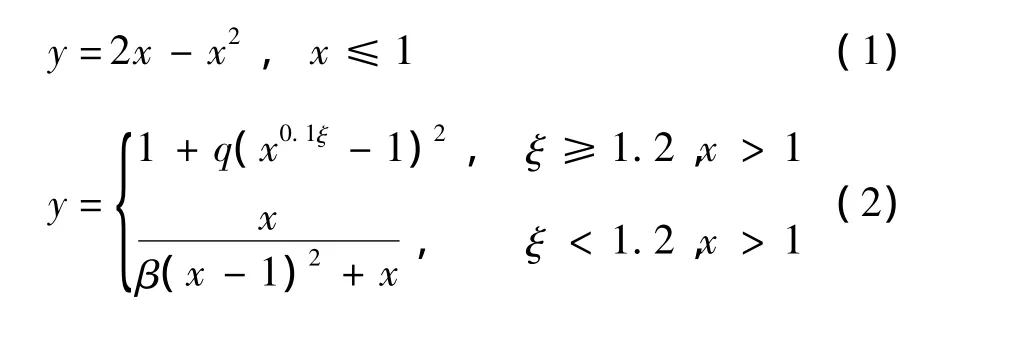
式中:

σc和εc分别为混凝土应力和应变;σc0和εc0分别为混凝土峰值应力和应变;ξ=(Asfy)/(Acfck)为钢管混凝土套箍系数，其中As和Ac分别为钢管面积和钢管内混凝土面积，fy和fck分别为钢材屈服强度和混凝土棱柱体轴心抗压强度;f'c为混凝土圆柱体轴心抗压强度;εcc、β、q为计算过程中间值;με为微应变符号.

忽略混凝土的受拉作用对于计算薄壁圆钢管混凝土柱的压弯承载力可能会偏于保守，文中计算时考虑混凝土受拉对截面抗弯的贡献.混凝土纤维的受拉本构采用双折线模型，抗拉强度，极限拉应变取10倍峰值拉应变，具体见文献［18］;钢材采用理想弹塑性模型，不考虑其硬化作用.混凝土纤维及钢材纤维的单轴本构模型如图1所示.

图1 混凝土与钢材纤维的单轴本构模型Fig.1 Uniaxial constitutive models of concrete and steel fibers

1.2 废弃混凝土块体的随机生成和投放

由于薄壁圆钢管再生混合柱内的新、旧混凝土混合体受到外侧钢管的约束，其界面缺陷可在一定程度上得到抑制.为简化起见，文中假定薄壁圆钢管再生混合柱内新、旧混凝土完全粘结，柱截面变形满足平截面假定，计算时不再单独考虑新、旧混凝土界面作用.

为分析废弃混凝土在截面上的不均匀分布对薄壁圆钢管再生混合柱受压力学性能的影响，文中采用了在纤维梁单元积分点截面上随机生成和投放废弃混凝土块体的技术，即将废弃混凝土块体简化为二维圆形区，按一定规则随机生成废弃混凝土圆形区后，再对其在钢管围成的圆形平面区域内进行随机投放，从而获得废弃混凝土块体在柱截面上随机分布的纤维网格，最后再利用纤维梁单元进行非线性计算.随机产生的混凝土纤维网格及纤维梁单元如图2所示.

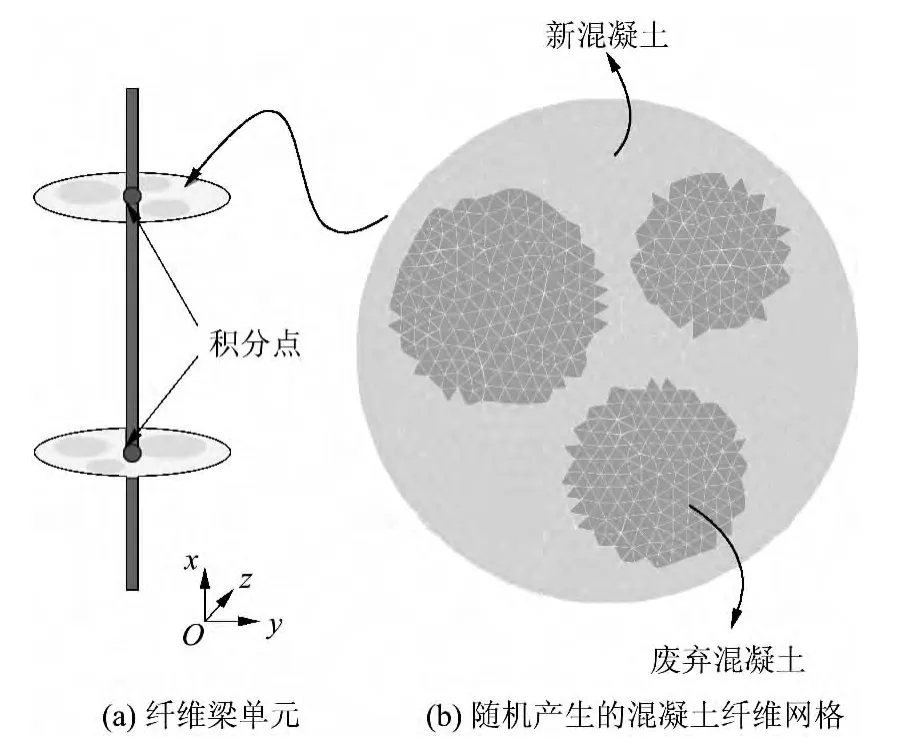
图2 纤维梁单元与随机产生的混凝土纤维网格Fig.2 Fiber beam element and randomly-generated fiber discretization of concrete

混凝土细观计算力学中，当在二维平面内生成随机骨料时，常假设骨料粒径分布服从某种分布［23］，如由富勒三维骨料级配曲线转化而成的瓦拉文二维骨料级配公式［24-26］.对于废弃混凝土块体，其性质和尺寸分布均不同于一般的混凝土骨料.根据试验观察，同时为简化起见，文中假定废弃混凝土圆形区直径服从正态分布，其均值为0.4Dint，标准差为0.1Dint，同时规定其最小值为0.2Dint，最大值为0.6Dint(Dint为圆钢管内径).此外，假定废弃混凝土圆形区的总面积等于柱截面混凝土总面积与废弃混凝土取代率(η)的乘积.

按上述规则随机生成废弃混凝土圆形区，记录各个圆形区的直径，再对其进行随机投放.具体步骤如下:

(1)采用Delaunay(狄洛尼)算法将投放区域(即积分点截面上钢管围成的圆形区域)划分为三角形网格，作为投放废弃混凝土圆形区的背景网格，同时记录各网格的编号和中心点坐标.为提高计算速度，网格尺寸不宜过小;但网格太大又达不到计算精度.经大量试算，发现三角形网格的特征尺寸取0.02Dint左右较为合适.

(2)对废弃混凝土圆形区按从大到小顺序进行排列，然后依次进行投放.采用随机数发生器生成一个随机数，该随机数的范围限定在三角形网格的编号范围内.投放某一废弃混凝土圆形区之前应先判断该随机数对应的三角形网格的中心能否作为待投放圆形区的圆心，判断条件为:在该位置放入待投放圆形区后，应使待投放圆形区圆心至投放区域边界的距离大于待投放圆形区半径，待投放圆形区圆心至任一已投放圆形区圆心距离大于两者半径之和.通过这两个判断条件，可保证待投放圆形区始终位于投放区域内，且不与已投放圆形区位置发生冲突.需要注意的是，有可能在投放某一圆形区时，投放区域内所有三角形网格都不满足以上判断条件，这一情况在废弃混凝土取代率较高、废弃混凝土圆形区较大时容易发生，此时应回溯至上次投放并重新执行该次投放.

(3)当所有废弃混凝土圆形区投放完成后，根据各个三角形网格中心点坐标，判断其属于废弃混凝土块体还是新混凝土.若三角形网格中心位于任一废弃混凝土圆形区之内，则认为该三角形网格(即纤维)是废弃混凝土，反之则认为其是新混凝土.

通过以上3个步骤，生成可考虑废弃混凝土圆形区在纤维梁单元积分点截面上随机分布的纤维网格，再按常规方法进行纤维梁单元计算.典型的随机生成的混凝土纤维网格见图2(b).

1.3 计算程序及验证

根据上述方法，采用C++语言编制了基于柔度法的、可考虑材料与几何双重非线性的纤维梁单元程序.几何非线性采用C.R.(共转)坐标列式，非线性方程组求解采用完全Newton-Raphson方法和位移控制加载，以方便得到荷载-位移曲线的下降段.程序编制时广泛采用C++标准模板库(STL)和“准”标准模板库(Boost)中的向量操作、排序、查找、时间中断设置、随机数生成等库函数［27］，以提高程序执行效率.

为验证程序计算的正确性，同时评价废弃混凝土在截面上的不均匀分布对薄壁圆钢管再生混合柱受压力学性能的影响，选用文献［8］的部分试验结果与程序计算结果进行对比.所选试件的基本参数如表1所示，试件的计算简图见图3.

表1 所选试件的基本参数1)Table 1 Basic parameters of selected specimens

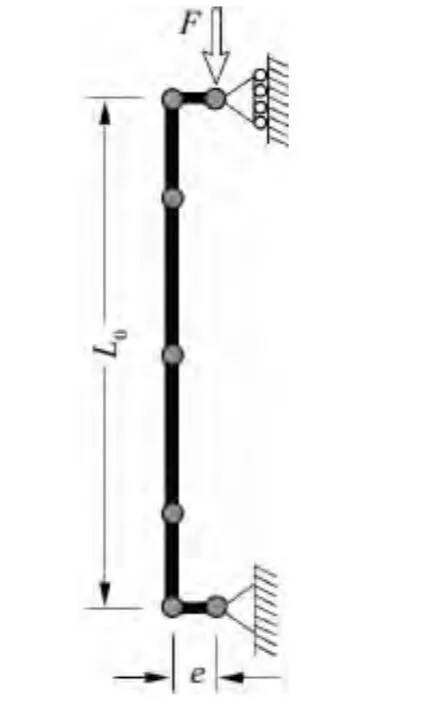
图3 试件计算简图Fig.3 Calculation sketch of specimens

计算时所有试件沿全柱高采用1个单元，单元上设置5个Gauss-Lobatto积分点(含试件上下两个端点).轴压试件计算时施加千分之一柱长的初始偏心距以考虑初始缺陷.对表1中的各试件采用Monte Carlo方法进行计算模拟，模拟次数为2000次［18］，每次模拟时均在纤维梁单元积分点截面上随机生成和投放废弃混凝土块体.试件计算结果与文献［8］中试验结果的对比如图4所示.图中“COV”为计算受压承载力的变异系数.

从图4中可以看出:

(1)总体来看，计算结果与实验结果吻合较好.试件计算承载力的最大、最小值基本能包络实测承载力，这表明考虑废弃混凝土在截面上的不均匀分布能更好地预测薄壁圆钢管再生混合柱的受压承载力.

图4 计算结果与文献［8］中试验结果的对比Fig.4 Comparisons of calculated results with measured results from Ref.［8］

(2)在其他参数相同的情况下，随着偏心距的增大，计算承载力的变化幅度和变异系数变化不大，但随着钢管壁厚的减小，计算承载力的变化幅度有所增加，这表明随着钢管壁厚的减小，废弃混凝土在截面上的不均匀分布对薄壁圆钢管再生混合柱的受压承载力影响增大.

(3)计算结果所表现出的柱子的初始刚度与实测结果所表现出的柱子的初始刚度基本重合，这表明是否考虑废弃混凝土的不均匀分布对预测薄壁圆钢管再生混合柱的初始刚度影响不大.

(4)试验结果所表现出的柱子的延性总体要比计算结果所表现出的柱子的延性好，这表明薄壁圆钢管再生混合柱的延性一般不低于计算预测值.另外还可以看出，是否考虑废弃混凝土在截面上的不均匀分布对预测薄壁圆钢管再生混合柱的峰值后弱化行为有一定影响，且随着钢管壁厚的减小该影响逐渐增大.

2 参数分析

以下主要考察柱子长径比、钢管壁厚、废弃混凝土取代率，以及其新、旧混凝土强度差对薄壁圆钢管再生混合柱受压承载力的影响.计算时取柱子外径D=400mm;计算长度L0=2000，4000，6000，8000，10000，12000mm;钢管壁厚t=2，4，8 mm;废弃混凝土取代率η=25%，33.3%，40%;新、旧混凝土强度等级C30/C35、C30/C40和C30/C45(“/”前、后分别为旧、新混凝土强度等级);钢材屈服强度fy= 350MPa.为方便起见，以编号“R#-T#-M#-C#/#”代表某一柱子，其中R、T、M分别表示柱子长径比、钢管壁厚和废弃混凝土取代率.以编号R10-T2-M33-C30/40为例，表示该柱子长径比为10、钢管壁厚为2mm、废弃混凝土取代率为33.3%、新、旧混凝土强度等级分别为C40和C30.

借鉴文献［28］，计算时对每个柱子取不同的偏心距e，然后按文中方法进行随机模拟，得到对应某一偏心距的柱子受压承载力的变化范围(即承载力的最大、最小值)，将这些值依次连接形成该柱子受压承载力随偏心距变化的带状曲线，通过这些带状曲线考察不同参数对柱子受压承载力的影响.

2.1 长径比对薄壁圆钢管再生混合柱受压承载力的影响

长径比对薄壁圆钢管再生混合柱受压承载力的影响如图5所示.由图5可见:偏心距较小时，长径比对薄壁圆钢管再生混合柱受压承载力的影响较为显著，后者随前者增大持续减小;随着偏心距的增加，不同长径比的薄壁圆钢管再生混合柱的受压承载力逐渐相等并趋于零;随着长径比的增加，柱截面内废弃混凝土的不均匀分布对薄壁圆钢管再生混合柱受压承载力的影响有所减小(即曲线带宽减小)，这主要是因为随着柱子长度的增加，其破坏模式逐渐变为弹性失稳，此时混凝土强度对承载力影响不大;随着偏心距的增加，柱截面内废弃混凝土的不均匀分布对薄壁圆钢管再生混合柱受压承载力的影响呈减小趋势，这主要是因为偏心距很大时(偏心距=∞即为纯弯状态)，柱子承载力将主要由钢管贡献，而混凝土对强度的贡献不大.

图5 长径比对薄壁圆钢管再生混合柱受压承载力的影响Fig.5 Influence of length-to-diameter ratio on compressive capacity of thin-wall circular steel tubular columns filled with DCBs and FC

2.2 钢管壁厚对薄壁圆钢管再生混合柱受压承载力的影响

钢管壁厚对薄壁圆钢管再生混合柱受压承载力的影响如图6所示.由图6可见:钢管壁厚对薄壁圆钢管再生混合柱受压承载力的影响显著，后者随前者增大持续增大;随着钢管壁厚的增加，柱截面内废弃混凝土的不均匀分布对薄壁圆钢管再生混合柱受压承载力的影响有所减小，这主要是因为钢管壁厚增加，其对承载力贡献的比例增大，而混凝土的贡献比例则随之减小.

图6 钢管壁厚对薄壁圆钢管再生混合柱受压承载力的影响Fig.6 Influence of steel tube thickness on compressive capacity of thin-wall circular steel tubular columns filled with DCBs and FC

2.3 废弃混凝土取代率对薄壁圆钢管再生混合柱受压承载力的影响

废弃混凝土取代率对薄壁圆钢管再生混合柱受压承载力的影响如图7所示.由图7可见:废弃混凝土取代率在25%～40%范围内变化时，柱截面内废弃混凝土的不均匀分布对薄壁圆钢管再生混合柱受压承载力的影响相差很小.

图7 废弃混凝土取代率对薄壁圆钢管再生混合柱受压承载力的影响Fig.7 Influence of replacement ratio of demolished concrete on compressive capacity of thin-wall circular steel tubular columns filled with DCBs and FC

2.4 新、旧混凝土强度差对薄壁圆钢管再生混合柱受压承载力的影响

新、旧混凝土强度差对薄壁圆钢管再生混合柱受压承载力的影响如图8所示.由图8可见:当新、旧混凝土强度差不超过15MPa时，柱截面内废弃混凝土的不均匀分布对薄壁圆钢管再生混合柱受压承载力的影响相差不大.

图8 新、旧混凝土强度差对薄壁圆钢管再生混合柱受压承载力的影响Fig.8 Influence of strength difference between new and old concrete on compressive capacity of thin-wall circular steel tubular columns filled with DCBs and FC

3 结论

文中以柔度法纤维梁单元模型为计算工具，对薄壁圆钢管再生混合柱进行计算模拟，在近似考虑了柱截面上废弃混凝土强度分布的不均匀性对薄壁圆钢管再生混合柱受压力学性能影响的基础上，分析了柱子长径比、钢管壁厚、废弃混凝土取代率，以及新、旧混凝土强度差等参数对薄壁圆钢管再生混合柱受压承载力的影响，得到如下结论:

(1)是否考虑柱截面内废弃混凝土的不均匀分布对预测薄壁圆钢管再生混合柱的初始刚度影响不大;

(2)是否考虑柱截面内废弃混凝土的不均匀分布对预测薄壁圆钢管再生混合柱的受压弱化行为有一定影响，且随着钢管壁厚的减小该影响逐渐增大;

(3)废弃混凝土取代率在25%～40%之间变化，或新、旧混凝土强度差不大于15MPa时，废弃混凝土不均匀分布对薄壁圆钢管再生混合柱受压承载力的影响相差不大;

(4)偏心距较小时，随着钢管壁厚或长径比减小，废弃混凝土不均匀分布对薄壁圆钢管再生混合柱受压承载力的影响有所增大;

(5)随着偏心距增加，废弃混凝土不均匀分布对薄壁圆钢管再生混合柱受压承载力的影响呈减小趋势.

［1］ Hansen T C.Recycling of demolished concrete and masonry，RILEM Report No.6［R］.Technical Committee 37-DRC Demolition and Reuse of Concrete，RILEM.Lond on:E＆FN SPON，1992.

［2］ 肖建庄.再生混凝土［M］.北京:中国建筑工业出版社，2008.

［3］ Limbachiya M，Meddah M S，Ouchagour Y.Performance of portland/silica fume cement concrete produced with recycled concrete aggregate［J］.ACI Materials Journal，2012，109(1):91-100.

［4］ Xiao J Z，Li W G，Fan Y H，Huang X.An overview of study on recycled aggregate concrete in China(1996—2011)［J］.Construction and Building Materials，2012，31 (6):364-383.

［5］ 吴波，刘琼祥，刘伟，等.钢管再生混合构件初探［J］.工程抗震与加固改造，2008，30(4):120-124. Wu Bo，Liu Qiong-xiang，Liu Wei，et al.Primary study on recycled-concrete-segment filled steel tubular members［J］.Earthquake Resistant Engineering and Retrofitting， 2008，30(4):120-124.

［6］ 吴波，刘伟，刘琼祥，等.钢管再生混合短柱的轴压性能试验［J］.土木工程学报，2010，43(2):32-38. Wu Bo，Liu Wei，Liu Qiong-xiang，et al.Experimental study on the behavior of recycled-concrete-segment/lump filled steel tubular stub columns subjected to concentrically axial load［J］.China Civil Engineering Journal，2010，43(2):32-38.

［7］ 吴波，刘伟，刘琼祥，等.薄壁钢管再生混合短柱轴压性能试验研究［J］.建筑结构学报，2010，31(8):22-28. Wu Bo，Liu Wei，Liu Qiong-xiang，et al.Axial behavior of thin-walled steel stub columns filled with demolished concrete segment/lump［J］.Journal of Building Structures，2010，31(8):22-28.

［8］ 吴波，赵新宇，张金锁.薄壁圆钢管再生混合中长柱的轴压与偏压试验研究［J］.土木工程学报，2012，45 (5):65-77. Wu Bo，Zhao Xin-yu，Zhang Jin-suo.Tests on slender circular thin-walled steel tubular columns filled with demolished concrete lumps under concentrically/eccentrically compressive loadings［J］.China Civil Engineering Journal，2012，45(5):65-77.

［9］ 吴波，赵新宇.混凝土再生混合构件的基本力学性能研究及应用［C］∥混凝土结构与材料新进展(第四届结构工程新进展国际论坛文集.北京:中国建筑工业出版社，2010.

［10］ Spacone E，El-Tawil E.Nonlinear analysis of steel-concrete composite structures:state of the art［J］.Journal of Structural Engineering，ASCE，2004，130(2):159-168.

［11］ Portolés J M，Romero M L，Filippou F C，et al.Simulation and design recommendations of eccentrically loaded slender concrete-filled tubular columns［J］.Engineering Structures，2011，33(5):1576-1593.

［12］ 陈滔.基于有限单元柔度法的钢筋混凝土框架三维非弹性地震反应分析［D］.重庆:重庆大学土木工程学院，2003.

［13］ Aval S B B，Saadeghvaziri M A，Golafshani A A.Comprehensive composite inelastic fiber element for cyclic analysis of concrete-filled steel tube columns［J］.Journal of Engineering Mechanics，ASCE，2002，128(4):428-437.

［14］ JBM de Sousa Jr，Caldas R B.Numerical analysis of composite steel-concrete columns of arbitrary cross section［J］.Journal of Structural Engineering，ASCE，2005，131(11):1721-1730.

［15］ Valipour H R，Foster S J.Nonlinear static and cyclic analysis of concrete-filled steel columns［J］.Journal of Constructional Steel Research，2010，66(6):793-802.

［16］ Tort C，Hajjar J F.Mixed finite-element modeling of rectangular concrete-filled steel tube members and frames under static and dynamic loads［J］.Journal of Structural Engineering，ASCE，2010，136(6):654-664.

［17］ Thai H T，Kim S E.Nonlinear inelastic analysis of concrete-filled steel tubular frames［J］.Journal of Constructional Steel Research，2011，67(12):1797-1805.

［18］ Lee T H，Mosalam K M.Probabilistic fiber element modeling of reinforced concrete structures［J］.Computers＆Structures，2004，82(27):2285-2299.

［19］ 李杰，范文亮.钢筋混凝土框架结构体系可靠度分析［J］.土木工程学报，2008，41(11):7-12. Li Jie，Fan Wen-liang.System reliability analysis of RC frames［J］.China Civil Engineering Journal，2008，41 (11):7-21.

［20］ Limkatanyu S，Spacone E.Reinforced concrete frame element with bond interfaces(I):displacement-based，force-based，and mixed formulations［J］.Journal of Structural Engineering，ASCE，2002，128(3):346-355.

［21］ Souza de R M.Force-based finite element for large displacement inelastic analysis of frames［D］.Berkeley: Department of Civil and Environmental Engineering，University of California，2000.

［22］ 韩林海.钢管混凝土结构——理论与实践［M］.北京:科学出版社，2007.

［23］ Bažant Z P，Tabbara M R，Kazemi M T，et al.Random particle model for fracture of aggregate or fiber composites［J］.Journal of Engineering Mechanics，ASCE，1990，116(8):1686-1705.

［24］ 刘光廷，王宗敏.用随机骨料模型数值模拟混凝土材料的断裂［J］.清华大学学报:自然科学版，1996，36 (1):84-89. Liu Guang-ting，Wang Zong-min.Numerical simulation study of fracture of concrete materials using random aggregate model［J］.Journal of Tsinghua University:Sci＆Tech，1996，36(1):84-89.

［25］ 宋玉普.多种混凝土材料的本构关系和破坏准则［M］.北京:中国水利水电出版社，2002.

［26］ 马怀发，陈厚群，黎保琨.混凝土试件细观结构的数值模拟［J］.水利学报，2004，10(2):27-35. Ma Huai-fa，Chen Hou-qun，Li Bao-kun.Meso-structure numerical simulation of concrete specimens［J］.Journal of Hydraulic Engineering，2004，10(2):27-35.

［27］ 罗剑锋.Boost程序库完全开发指南——深入C++“准”标准模板库［M］.北京:电子工业出版社，2010.

［28］ Mirza S A，Skrabek B W.Statistical analysis of slender composite beam-column strength［J］.Journal of Structural Engineering，ASCE，1992，118(5):1312-1332.