基于遗传算法的有源电力滤波器直流母线电压控制

韩学栋，王海华

(江苏省电力设计院，江苏南京211102)

将式（10）代入式（9）中，可得：

如今电力电子装置已遍布人们的生产生活中，但其自身所具有的非线性使得电网的电流和电压发生畸变，这些非线性设备的数量和容量的日益增大将对电网的正常运行以及电力设备的安全造成影响和危害。为抑制非线性设备谐波污染，出现了诸多解决谐波问题的方法，有源电力滤波器（APF）是其中一种较好的谐波抑制技术[1-4]。对于APF来说，若直流侧电压产生较大的波动，会导致APF不能正常工作，并且还可能危及设备的可靠运行。因此，控制电路除了使APF的输出能快速准确跟踪指令电流变化之外，还需要使主电路直流侧电压保持稳定。遗传算法是模拟自然界遗传机制和生物进化论而成的一种并行随即搜索最优化方法[5]，文中将结合遗传算法实现APF中PI控制器调节系数的优化设计，以实现直流侧母线电压的稳定控制。

1 APF原理及其数学模型

1.1 APF的原理及特点

APF是一种动态抑制谐波和补偿无功的电力电子装置，能对不断变化的负载谐波电流进行实时补偿，其工作原理如图1所示。

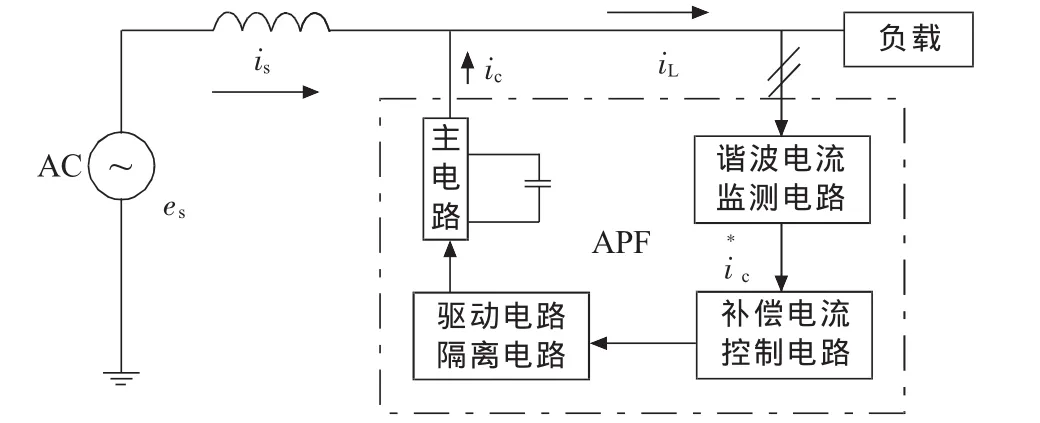
图1 APF基本工作原理

当需要补偿负载所产生的谐波电流时，APF检测出补偿对象负载电流iL的谐波分量，将其作为补偿电流的指令信号，由补偿电流发生电路产生的补偿电流ic即与负载电流中的谐波分量ilh大小相等，也就是说，电源只向负载提供基波电流，而谐波电流由APF的补偿电流发生电路提供，从而使得交流电源电流is中只含基波，不含谐波，这样就达到了抑制电源电流中谐波的目的[6-8]。

在理想情况下，APF输出的补偿电流中不含有基波有功分量，直流侧母线电压恒定不变，补偿装置功率平衡。但实际情况中，当开关器件功耗引起直流母线电压的降低、网侧电压畸变且负载不对称、谐振过电压通过逆变器及续流二极管向直流侧电容充电以及APF检测环节的延时等一系列因素都将引起补偿装置的功率不平衡[9-11]。

1.2 APF的数学模型

根据有功功率平衡原理确定补偿器的近似数学模型，对系统稳态和动态特性进行分析，并为下一节运用遗传算法确定PI参数提供被控对象的数学模型。

该数学模型的建立基于以下假设：

（1）只有电流的基波分量影响平均功率的平衡，而谐波分量不影响功率平衡；

（2）电网电压平衡且不包含谐波；

（3）逆变器输入端缓冲电感的电阻和电感，以及系统线路的电阻和电感采用集中参数R，L表示，所有损耗都集中在R上。

系统结构如图2所示。假设系统结构对称，在不考虑谐波的情况下，三相可简化为一相进行分析，以下对a相进行数学模型的推导，将a相电网电流写成向量的形式：

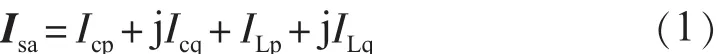
式中：Icp，ILp分别为APF补偿电流中的有功电流有效值和负载有功电流有效值（A）；Icq，ILq分别为APF补偿电流中的无功电流有效值和负载无功电流有效值（A）。

当负载一定时，由于无功功率仅在有源滤波器与负载之间进行交换，可以认为稳态时jIcq=-jILq，所以电

由式（3—5）、（7）、（8）可得：

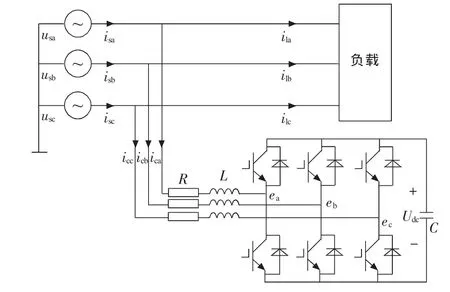
图2系统结构

网电流为：

由上式可知，输入补偿之路的平均有功功率Pc可以表示为：

式中：PR为等效电阻R上损耗的功率；Pind为支路电感的储能功率；Pcap直流侧电容储能功率。其中：

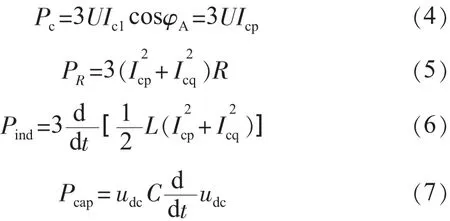
式中：udc为直流侧电容电压。

当负载确定后，即ILq确定，由于ILq与Icq大小相等，方向相反，所以Icq为常数。此时，对Pind的影响取决于 Icp，故式（6）可改写为：

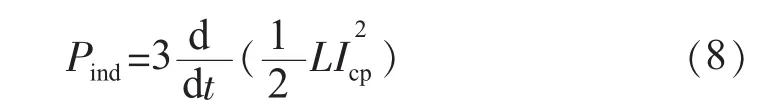
式中Icp和udc可改写成稳态值与变化量之和的形式：

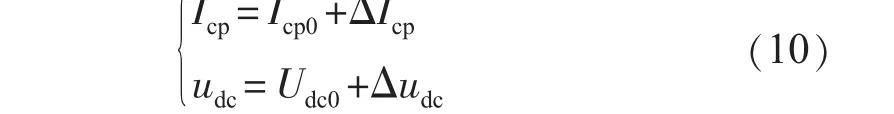
将式（10）代入式（9）中，可得：

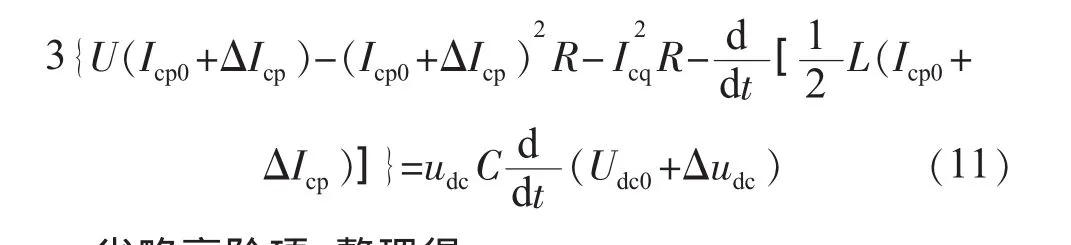
省略高阶项，整理得：由式（9）可以

得到稳态方程：

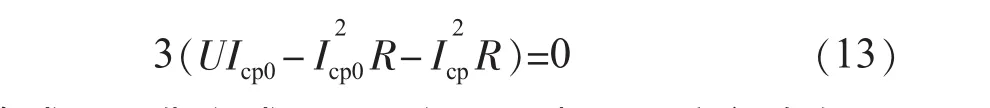
将式（13）代入式（12）可得 Δudc与 ΔIcp之间有如下关系：

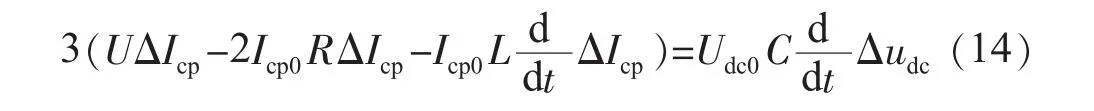
由式（14）得到频域下APF的传递函数：

式中：

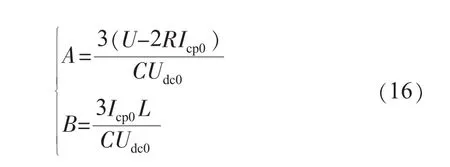
式（15）为APF的近似数学模型，由此模型可通过遗传算法确定系统的PI参数。

2基于遗传算法的PID整定原理

遗传算法具有对参数编码进行操作、可多点并行操作、通过目标函数进行适配值的计算、寻优规则由概率决定等优点。

2.1遗传算法的计算原理

遗传算法在操作时首先确定参数范围，再根据精度的要求，对其进行二进制编码。由此编码得到的字串为遗传算法可以操作的对象，同时，通过计算机随之产生初始种群，种群大小视计算的复杂程度而定。

计算过程中如果着重追求系统的动态性能，得到的参数可能使控制信号偏大，进而导致系统不稳定。鉴于适应函数与目标函数相关，在目标函数确定后，可直接将其作为适配函数进行参数寻优，以防止得到的参数造成系统不稳。

2.2遗传算法的操作

首先通过适配函数求得适配值，进而求每个串对应的复制概率。复制概率与每代字串个数的乘积为该串在下一代中应复制的个数。复制概率大的在下一代中将有较多的后代，相反则被淘汰。其次进行单点交叉，交叉概率为Pc，最后以概率Pm进行变异。

初始种群通过复制、交叉及变异得到了新一代种群，该代种群经解码后代入适配函数，观察是否满足结束条件，若不满足，则重复以上操作直到满足为止。操作过程如图3所示。

利用上述遗传算法的操作过程实现PI调节系数kp，ki的最优解析。

2.3 APF的传递函数

欲通过遗传算法进行PI参数的整定，需确定APF具体的传递函数。传递函数的形式如式（15）所示，A与B 的表达如式（16）所示。 式（16）中：

图3遗传算法流程

（1） U为一相电压有效值，系统中U=220 V；

（2） R为输出电路的等效电阻，系统中R=1 Ω；

（3） Icp0为a相补偿电流有功分量的稳定值分量，系统中Icp0=1.27 A；

（4） C为直流侧电容值，系统中C=700 μF；

（5）Udc0为直流侧电压的稳定值分量，系统中Udc0=1200 V；

（6） L为APF输出电感，系统中L=3 mH。

计算可得：A=776.62，B=0.016 3。 所以，APF 的传递函数为：

采样时间为1 ms，输入指令为一阶跃信号。

3仿真分析

为获取满意的过渡过程动态特性，采用误差绝对值时间积分性能指标作为参数选择的最小目标函数。为了防止控制量过大，在目标函数中加入控制输入的平方项。选用下式作为参数选取的最优目标：

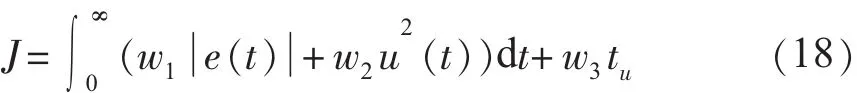
式中：e（t）为系统误差；u（t）为控制器输出；tu为上升时间；w1，w2，w3为权值。为了避免超调，采用了惩罚功能，即一旦产生超调，将超调量作为最优指标的一项，此时最优指标为：

式中：w4为权值，且w4＞＞w1。APF的仿真系统如图4所示。

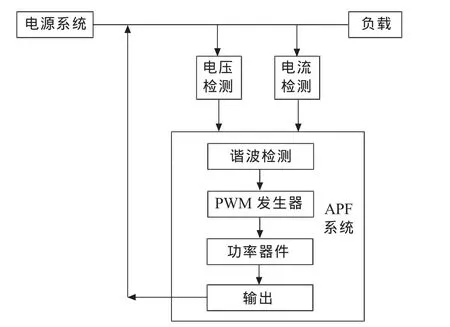
图4有源滤波仿真系统

根据图3所示的遗传算法流程图以及式 （19），在MATLAB中进行编程。遗传算法中使用的样本个数定为30，交叉概率和变异概率分别为Pc=0.9，Pm=0.033。根据经验值，参数kp的取值范围为[0，1]，ki的取值范围为[0，1]，取 w1=0.999，w2=0.001，w3=2.0，w4=100。 采用实数编码方式，经过100代进化，获得的优化参数为：kp=0.061，ki=0.053。

性能指标J=219.749 6，代价函数的优化过程和采用整定后的PI控制阶跃响应如图5、图6所示。

图6 PI的阶跃响应曲线

将经遗传算法计算出的kp，ki值代入到APF仿真系统模型中，对直流侧电压进行PI稳定控制，可得直流侧电压的仿真响应曲线，如图7所示。同时，针对相同的APF仿真系统模型，对其PI调节器参数进行传统方式的调节，在经过多次修正更改PI值后，得出直流侧电压的仿真曲线，如图8所示。

图7基于遗传算法的直流侧电压响应曲线

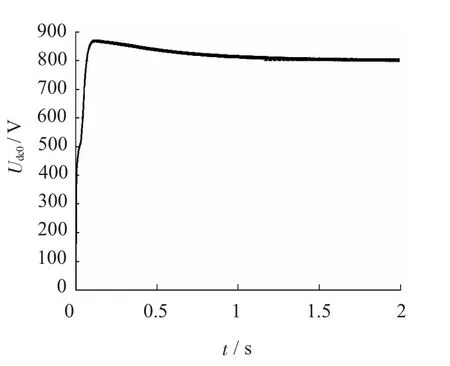
图8基于传统算法的直流侧电压响应曲线

由图7可知，其直流侧电压的响应曲线在0.07 s时达到预设电压值800 V，超调量为25.5/800=3.2%，调节时间为0.11 s，然后进入稳定状态，APF直流侧电压稳定在800 V。在传统PI调节的方式下，由图8可知，直流侧电压响应在1.5 s左右才达到预设电压值，且其超调量约为8.4%，由此可知，基于遗传算法的仿真系统具有更好的动态性能，且在PI参数的整定时间上少于传统方法。

4结束语

介绍了并联电压源型APF的工作原理，指出了影响其直流侧电压稳定的几个因素，推导了电压源型有源电力滤波器的数学模型，介绍了遗传算法的原理并给出了遗传算法的操作流程图，在此基础上，以一个具有并联电压源型APF的系统为例，通过遗传算法优化计算出了该系统中APF的PI调节器的调节系数，通过MATLAB/simulink仿真得出了在优化后的PI调节参数下直流侧电压响应曲线，验证了该方法的合理性，为遗传算法在PI整定方面的研究提供了借鉴。

[1]钟 山，杨 晟，赵争鸣.有源电力滤波器技术与发展综述[J].变频器世界，2011（1）：45-49.

[2]张汉梅.有源电力滤波器综述[J].装备应用与研究，2011（12）：67-69.

[3]孙文华，陈 龙，袁晓冬.冶金企业集中接入配网的谐波影响及对策分析[J].江苏电机工程，2013，32(3)：46-49.

[4]彭海燕，王 宏.有源电力滤波器的原理介绍及应用[J].华北电力技术，2010（1）：35-37.

[5]刘金琨.先进PID控制及其MATLAB仿真[M].北京：电子工业出版社，2006：130-157.

[6]杜太行，胡相彬，赵 川，等.有源电力滤波器补偿电流控制与主电路参数设计[J].低压电器，2010（6）：51-56.

[7]车蓉蓉，徐 蓉.一种单相电路谐波及无功电流实时检测方法[J].江苏电机工程，2013，32(4)：41-43.

[8]于晶荣，滕召胜，章 兢，等.有源电力滤波器预测电流控制与稳定性分析[J].电工技术学报，2009，24(7)：164-170.

[9]庄伟雄，何益宏.有源电力滤波器直流侧电压控制系统的仿真[J].系统仿真学报，2012，24(5)：979-983.

[10]谢 斌，戴 珂，张树全，等.并联型有源电力滤波器直流侧电压优化控制[J].中国电机工程学报，2011，31(9)：23-29.

[11]李智华，刘 振，吕振彬.有源电力滤波器直流侧电压的模糊自适应控制[J].电源技术，2010，34(6)：582-585.