信号模型简化对雷达仿真误差的影响

徐群凤,李建勋,朱 峰

(1.上海交通大学电子信息与电气工程学院,上海200240;2.上海机电工程研究所,上海201109)

0 引言

在防空导弹武器系统仿真中,为了逼真地呈现探测的目标及其环境,考核其在干扰环境条件下系统的工作性能,需要对武器系统配置的雷达进行数学仿真。即通过在计算机上建立数学模型,模拟战场环境下雷达电磁信号环境和雷达系统,来仿真评估雷达的性能及其对整个武器系统的影响。相对于雷达功能仿真,信号仿真包含幅度和相位信息,可复现复杂的电磁环境和雷达处理的全过程,但雷达信号仿真系统的运算量大。本文仿真的雷达原型为相控阵雷达,采用LFM信号。在建模时,为保证仿真系统在计算机上运行的实时性,采用单频信号(窄脉冲无调制信号)代替实际雷达的LFM信号,以省略脉冲压缩时间[1]。对于相控阵雷达,LFM信号中不同频移会引起方向图的移动,单频信号波束指向则固定。电磁波在传播过程中,照射海面产生具有多普勒频谱的海杂波[2],同样,LFM信号通过海面反射回雷达目标回波,其频谱分量也远比单频信号复杂。因此,有必要对信号简化可能引起的仿真误差进行分析。

1 LFM信号及其匹配滤波模型

在视频信号仿真中,雷达发射的LFM信号形式为[3]

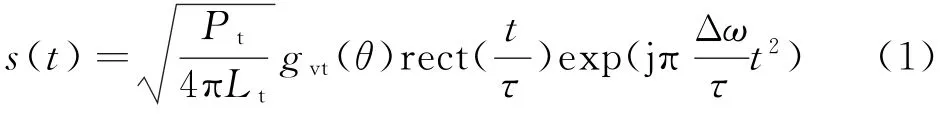
式中,Pt为发射机峰值功率;Lt为发射综合损耗;gvt(θ)为发射天线方向图(电压增益);Δω为调频带宽;τ为脉冲宽度。

匹配滤波是以输出最大信噪比为准则的最佳线性滤波器,根据最佳接收信号理论可知,为了在接收装置输出端获取最大信噪比,匹配滤波器的幅度特性应与信号谱密度一致,而相位特性曲线与信号相位特性相反。基于实现角度考虑,仿真中采用频域FFT法,实现LFM信号的匹配滤波。

首先,生成信号采样为

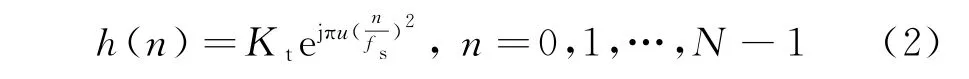
式中,u为调频斜率;fs为采样频率;N=fsτ为脉冲采样点数;Kt为匹配滤波函数系数。然后,将h(n)进行FFT变换,得到H(k),H(k)的共轭即为所需匹配滤波器的频域响应。雷达接收端输入信号sr(t)的FFT变换为Sr(k),最终输出为

将上述So(k)进行逆FFT变换即可得到输出序列so(n)。

2 对距离探测威力的影响

对于采用电扫描天线的雷达,波束最大值指向θ是信号波长λ,即频率f的函数。当移相器相移值ΔΦB固定时,波束指向为

当信号频率改变时,波束指向随之改变,改变量为

当雷达信号采用LFM信号时,脉冲内信号频移带动方向图移动,如图1所示。

由图1可以看出,如果信号接收方向与方向图中心位置重合,则接收信号的幅度变化很小;如果信号接收方向偏离方向图中心,则信号幅度的相对变化也随之增大。导致接收脉冲的包络形状大

致按直线定律产生变化,如式(6)所示。

式中,c为脉冲顶部斜率。信号幅度谱如图2中虚线所示,实线表示脉冲顶部水平的信号频谱,两种信号的相位谱相同。

图1 LFM信号5个频率上的方向图

图2 接收信号频谱

由匹配滤波理论可知,接收脉冲的波形偏离矩形会导致匹配滤波器输出端信号能量的损耗,对雷达探测威力产生影响。将图2中两种信号输入匹配滤波器,经计算,输出的脉冲信号幅度是一致的。分析是由于图2中顶部水平与顶部倾斜信号的平均幅度相同,而顶部水平信号相当于LFM信号通过图1中间频率对应方向图产生的接收端输入,该频率为LFM信号的中心频率。由此可得出如下结论：当仿真时用LFM信号中心频率的单频信号代替LFM信号时,对探测距离无影响。

首先是“三端发力”。源头端主动调结构减少磷石膏的排放量；中端把磷石膏作为重要的资源来管理，打造良好的品质，为下游利用创造良好的条件；末端就是把磷石膏利用这篇文章做好。

3 对海面目标回波特性的影响

为了仿真舰载三坐标雷达系统探测低空飞行目标,需要建立雷达目标回波信号模型[4]。当雷达探测低空掠海飞行的目标时,从目标反射回的雷达电磁波一部分以直射波的形式回到雷达接收机;还有一部分电磁波会投射到海面产生反射波,其中一部分反射波可从不同的仰角方向传播到雷达位置,如图3所示。

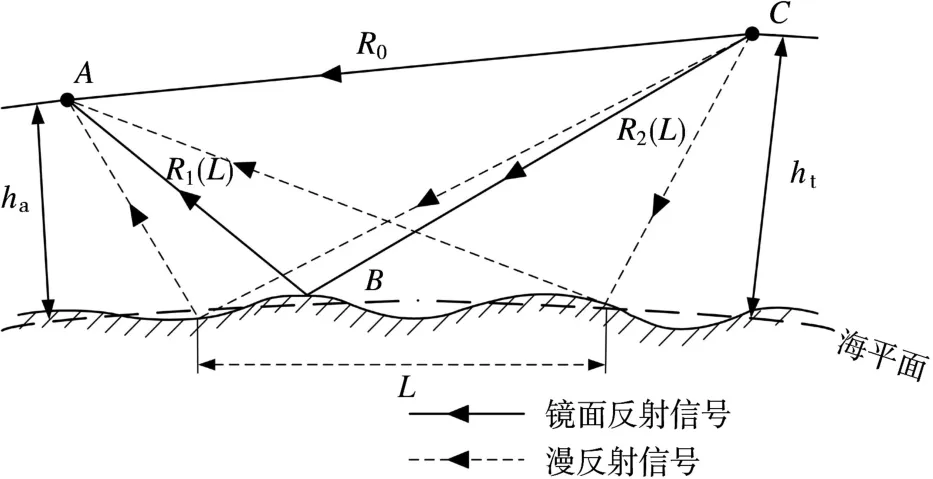
图3 目标回波组成

从海面反射回的目标回波信号分为镜像反射信号和漫反射信号。相对于镜像反射,漫反射随着入射余角、海浪起伏特性等变化而产生幅度和相角的变化,造成频谱展宽现象。LFM信号的宽带特性,使其从海面反射回的目标回波具有比单频信号更复杂的频谱,下面对此进行分析。

式中,M为LFM信号带宽范围内取样的频率点数目;A i为在频率ωi上来自目标信号的复振幅;L,R0,R1,R2含义见图3。第一项是以直线传播路径到达接收点的目标信号;第二项是从海浪表面反射回接收点的所有信号,从海表面反射回波以频率分量形式可表示为。A i0为频率ωi上的镜面反射回波,a ij为频率ωi上的漫发射回波分量。通过计算镜像反射和漫反射路程可得各分量值。

镜面反射点与雷达的水平距离G1可通过解下列方程式[5]获得：

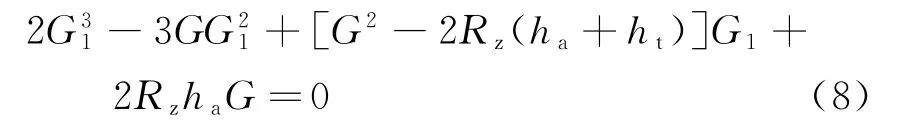
式中,Rz=8 500 km为修正为正常无线电波折射后的地球有效半径;ha为雷达天线距海面的高度;ht为目标距海面的高度;G为目标距雷达的水平距离。

对经海面多路径反射回雷达的信号频谱进行仿真计算,计算参数选取为在3级海情下(浪高取值为0.6 m),天线高度为20 m,目标高度为10 m,波长为15 cm,随着目标与雷达的距离不同,部分仿真结果如图4所示。图中横坐标表示漫反射相对于镜像反射的相角,纵坐标表示归一化幅度。由图中可以看出,当目标距离越近时,频谱展宽现象越明显,这是由于雷达目标距离越近时,不同反射路径的距离差变大引起的。

图4 海面反射目标回波的立体谱

图5 LFM信号匹配滤波器输出

图6 示出了中心频率为ω0的单频信号的输出,以及LFM信号通过匹配滤波器的输出。从图中可以看出,在直到视距的距离范围内,输出的信号幅度是没有差别的。

图6 LFM信号和单频信号的输出比较

4 结束语

在利用PC机实现雷达的信号仿真中,实时性是设计的重要因素。在针对某相控阵雷达探测海面低空飞行目标建立回波模型时,本文采用单频信号代替LFM信号,并分析了其对探测威力和传播特性仿真的影响。可得出如下结论：信号模型的简化将引起回波包络和频谱的变化,但对探测仿真结果无影响。仿真系统通常是实际系统某种程度的近似,本文的误差分析思想在构建系统仿真模型、评估仿真系统近似程度时具有一定的借鉴作用。

[1]于宵晖,罗鹏飞.线性调频脉冲压缩雷达视频回波模型[J].雷达科学与技术,2010,8(2)：101-103,108.YU Xiao-hui,LUO Peng-fei.Research on Simulation of LFM Pulse Compression Radar Return[J].Radar Science and Technology,2010,8(2)：101-103,108.(in Chinese)

[2]丁昊,李建忠,安昕,等.实测海杂波数据的多普勒谱特性[J].雷达科学与技术,2012,10(4)：400-408.DING Hao,LI Jian-zhong,AN Xin,et al.Doppler Spectra Property of Measured Sea Clutter Data[J].Radar Science and Technology,2012,10(4)：400-408.(in Chinese)

[3]王雪松,肖顺平,冯德军,等.现代雷达电子战系统建模与仿真[M].北京：电子工业出版社,2010：209-216.

[4]钟娟,刘以安,吴少鹏,等.舰载雷达低空目标回波信号仿真研究[J].雷达与对抗,2004(3)：1-5.

[5]SKOLNIK M I.雷达手册[M].王军,林强,米慈中,等译.北京：电子工业出版社,2003：49.