数值模拟在研究透水混凝土性能影响因素中的运用

魏勇，左文銮，张宏明，陈雷，范建峰

（南通众润混凝土有限公司利废技术开发中心，江苏 南通 海安 226600）

数值模拟在研究透水混凝土性能影响因素中的运用

魏勇，左文銮，张宏明，陈雷，范建峰

（南通众润混凝土有限公司利废技术开发中心，江苏 南通 海安 226600）

采用两水平析因试验设计 (Two-level factorial design) 和响应曲面法 (RSM) 定量研究了水灰比 (W/C)、骨料级配 (G)及水泥用量 (C) 对透水混凝土的空隙率 N0、有效空隙率 Ne、透水系数 K 及抗压强度 (f7d，f28d) 的影响，并建立了相应的数学模型。结果表明：在其他条件相同的情况下，随着水灰比 (W/C) 的增大，透水混凝土的空隙率 N0、有效空隙率 Ne及透水系数 K减小；随着石子级配 (G) 的增大，透水混凝土的空隙率 N0、有效空隙率 Ne及透水系数 K 增大；水泥用量 (C) 越多，透水混凝土抗压强度 (f7d，f28d) 越高。运用所得模型进行配合比优化，能得到满足要求的透水混凝土配合比。。

透水混凝土；两水平析因设计；响应曲面法；配合比优化

0 引言

近些年来，随着我国城镇化步伐的加快，绝大多数的城镇道路被各种不透水的混凝土所覆盖，使雨水等形成的地面水流只能通过城市地下排水系统排除，这对地下排水系统是个巨大考验，时常就有城市道路大面积积水给居民出行带来不便的报道。同时，由于不透水的混凝土的存在，地下水得不到及时的补充，水位线下降，造成大面积的干旱。其实解决问题的方法也很简单，只需将不透水的混凝土改成透水的问题就解决了。

100多 年前，英国就有透水混凝土的应用记载[1]。上世纪六七十年代，美国[1]、日本[2]先后对透水混凝土的性能进行了研究，陆续推出了一系列的国家级标准，并在一些工程中应用。相比国外，我国透水混凝土的研究起步较晚，上世纪90年代研究才逐步展开。已在一些工程中得到到了运用，但与发达国家相比还相差较远，仍然有很多理论研究与实际应用的问题有待解决。已有很多报道研究了水胶比、骨料及水泥用量三者对透水混凝土性能的影响，例如 M. Sonebi[3]采用两水平(最大值和最小值)析因设计（Two-level factorial design）方案研究了水灰比大小，骨料数量及水泥用量对透水混凝土各种性能的影响；徐仁崇[4]利用田口试验设计方法研究了水泥用量、石子级配及水灰比对透水系数和 28d 抗压强度的影响，但这些研究都缺少骨料级配这一类型因素在所建模型中对透水混凝土性能的定量影响研究。因此，本论文工作重点是要用数值模拟的方法定量研究骨料级配与另外两因素(水泥用量、水灰比)，对透水混凝土的空隙率、有效空隙率、透水系数及抗压强度的影响，并希望通过建立的模型获得所需要求下各石子级配配制透水混凝土的最佳配合比。

1 试验

1.1 原材料

水泥：采用盘固水泥集团有限公司生产的 P·II52.5 水泥，其主要技术指标如表 1 所示。

表 1 P·II52.5 水泥的主要技术指标

粗骨料：采用江苏省无锡市宜兴的碎石，将其筛分成2.36 ～4.75mm 和 9.5～16.0mm，石子的基本性能参数如表 2所示。

表 2 石子的基本性能参数

减水剂：采用江苏苏博特新材料股份有限公司生产的 SBTJM®-10 (缓凝、泵送)混凝土高效减水剂，减水率16.5%。

水：自来水。

1.2 试验方法

1.2.1 透水混凝土试块的制备

将碎石筛分成 2.36～4.75mm 和 9.5～16.0mm 足够的量，分别储存以待试验用；按配比称取上述碎石与 50% 的水预先搅拌 30s，其后倒入水泥再搅拌60s，最后将剩余的50% 的水及减水剂一起加入搅拌 60s；将拌合物分两层装入(100×100×100)mm 的试模中，每层用捣棒从四周向中心插捣 15 下，抹平表面后将试模放入标准养护箱中养护 2d，拆模后将试块移入标准养护室中继续养护至龄期。

1.2.2 透水混凝土性能测试

新拌透水混凝土的坍落度的测试按照 GB/T 50080－2002《普通混凝土拌合物性能试验方法标准》中关于坍落度测试的方法进行，本测试的目的为了保证拌合物状态相近，即以能够保持坍落度筒形状，骨料表面有光泽的状态为准，如图 1所示。

图 1 透水混凝土拌合物坍落度测试

空隙率和有效空隙率的测定按照量体积法[5]进行，先用游标卡尺量出规整试块的几何参数，然后计算试块的体积，最后按计算式 (1)、(2) 及 (3)[5]分别计算空隙率及有效空隙率。

式中：

n0——规整试块的空隙率，%；

ne——规整试块的有效空隙率，%；

ρs——多孔混凝土的体积密度，kg/m3，ρs= m2ν；

ρt——多孔混凝土的理论密度，kg/m3；

m1——在水中测得的试件浸水 24h 后的质量，kg；

m2——在 60℃ 的烘箱中烘 24h 后的质量，kg；

v——用游标卡尺测得的规整试块的体积，m3；

ρw——水的密度，kg/m3；

Pc——水泥与集料质量比；

ρc——水泥的密度，kg/m3；

ρ——集料的表观密度，kg/m3。

透水系数的测定采用固定水位高度法[6]，将成型面作为透水测试面，其余 4 个面用水泥浆密封，测量水经过透水混凝土试块由 180mm 降至 0 所用的时间 t，透水系数可由计算式 (4) 计算得到:

式中：

v ——透水系数；

h ——水位线高度，取 180mm；

t ——水通过透水混凝土试块所用的时间，s。

透水混凝土抗压强度的测试按照 GB/T 50081—2002 《普通混凝土力学性能试验方法标准》中关于混凝土抗压强度测试的方法进行。

1.3 试验设计

本论文采用两水平(最大值和最小值)的析因设计 (Twolevel factorial design)[7]的试验方案来研究各透水混凝土因子(水灰比、骨料级配、水泥用量)对透水混凝土的空隙率、有效孔隙率、透水系数及抗压强度的影响。其中透水混凝土性能影响因子水灰比、水泥用量为数值型变量，骨料级配为类型变量，因此试验次数为 23+2=10 次。具体的试验编码及参数设计如表 2、3 所示。

表 2 试验的设计参数

表 3 试验透水混凝土配合比

2 试验结果与讨论

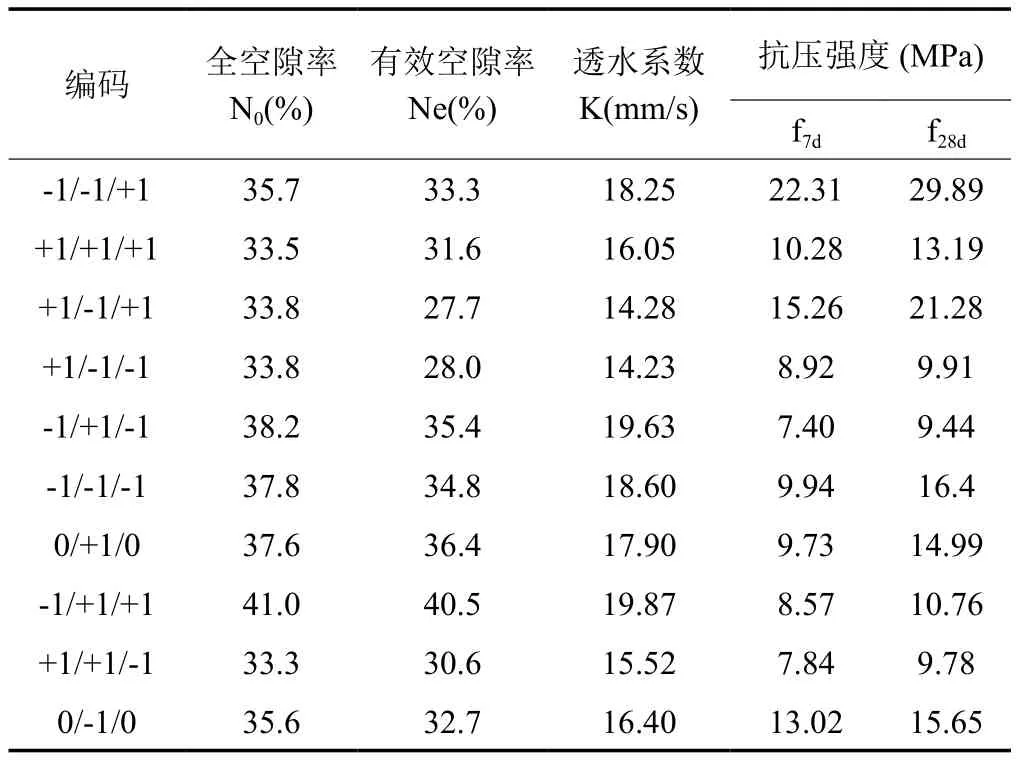
表 4 透水混凝土的性能参数

2.1 回归方程

析因试验设计的模k型回归方程表达式为:

式中：

y ——响应值；

αk0，αi，αij—— 各独立变量的响应回归系数；的线性效应；的交互作用；

ε——随机误差。

首先，假设与混料设计相关的用于多元线性回归分析的系数符合正态分布的假设。用模型拟合透水混凝土的空隙率N0，有效空隙率 Ne，透水系数 K，抗压强度（f7d，f28d），其用编码值（Coded Value）表示的回归方程为：

由上述回归方程可知方程的拟合系数 R2均高于 0.87，说明模型能较好的反应各因子对观察变量的影响，同时也进行了方差（ANOVA）显著性分析。F 值（F Value）是方差显著性分析中的一个重要指标，F 值越大，p 值（p-value）越小，正确的概率越高。一般认为，p＜0.01 表明结果非常显著，p＜0.05 表明结果比较显著，p＜0.1 表明结果显著。模型各参数的方差显著性分析如表 5 所示。在置信水平为 0.90 的情况，下表 5 中各参数、模型及残差的正态概率图（图略） ，均表明拟合效果较好。

表 5 模型各参数的方差显著性分析

2.2 响应曲面线分析透水混凝土性能

从此以后，那帮穿半头鞋子的人就再没有来和祥轩找过事。张满春也因此在和祥轩立住了脚根。为了答谢，和祥轩老板破例给了张满春一笔不菲的犒赏，外加一份店里的层银。因为他知道，张满春既然能把那帮人治下，也就可以指使他们卷土重来。为何不好好稳住他呢。这才是和祥轩最大的利润。

采用响应曲面法（Response Surface Methodology，RSM）分析透水混凝土的空隙率 N0，有效空隙率 Ne，透水系数 K，抗压强度（f7d，f28d）。通过回归方程 (6)～(10) 得到响应面等高线图。

2.2.1 透水混凝土的空隙率N0

由表 5 可知，透水混凝土的空隙率 N0大小显著受水灰比 (W/C)、石子级配 (G) 的影响；由公式 (6) 可知，影响透水混凝土的空隙率 N0大小顺序为：水灰比 (W/C)＞石子级配 (G)（-2.29∶0.69），石子级配 (G) 对透水混凝土的空隙率 N0大小的贡献比水灰比 (W/C) 小约 70%。因此，影响透水混凝土的空隙率 N0大小的最主要因素是水灰比 (W/C)。从图 2、3可看出，在其他条件相同的情况下，随着水灰比 (W/C) 的增大，透水混凝土的空隙率 N0减小。例如，当石子级配固定为2.36～4.75mm，水泥用量为 320kg/m3，水灰比从 0.25 增大到0.35 时，透水混凝土的空隙率 N0从 37.8% 降至 33.8%；同样当石子级配固定为 9.5～16.0mm，透水混凝土的空隙率 N0从38.2% 降至 33.3%。然而在其他条件相同的情况下，随着石子级配 (G) 的增大，透水混凝土的空隙率 N0增大。例如，当固定水泥用量为 340kg/m3，水灰比从 0.25 增大到 0.35 时，石子级配为 2.36～4.75mm 的透水混凝土的空隙率 N0从 35.6% 降至 33.8% 小于石子级配变为 9.5～16.0mm 的透水混凝土的空隙率 N0从 41.0% 降至 33.5%。这说明随着水灰比的增大，水泥浆体体积的增大，水泥浆体逐渐填充到石子空隙中去，使透水混凝土的空隙率 N0减小；同时石子的级配越小，石子的空隙率越小，透水混凝土的空隙率 N0也越小。不同石子级配(G) 的情况下，水灰比 (W/C) 与水泥用量 (C) 对透水混凝土的空隙率 N0的影响如下图 2、3 所示。

图 2 透水混凝土的空隙率 N0等高线(石子级配 G：2.36～4.75mm)

图 3 透水混凝土的空隙率 N0等高线(石子级配 G：9.5～16.0mm)

2.2.2 透水混凝土的有效空隙率 Ne

由表 5 可知，透水混凝土的有效空隙率 Ne大小显著受水灰比 (W/C)、石子级配 (G) 的影响；由公式 (7) 可知，影响透水混凝土的有效空隙率 Ne大小顺序为：水灰比 (W/C)＞石子级配 (G) (-3.26∶1.8)，石子级配 (G) 对透水混凝土的有效空隙率 Ne大小的贡献比水灰比 (W/C) 小约 45%。从图 4、5 可看出，在其他条件相同的情况下，随着水灰比(W/C)的增大，透水混凝土的有效空隙率 Ne减小。例如，当石子级配固定为 2.36～4.75mm，水泥用量为 340kg/m3，水灰比从 0.25增大到 0.35 时，透水混凝土的有效空隙率 Ne从 33.3% 降至27.7%；同样当石子级配固定为 9.5～16.0mm，透水混凝土的有效空隙率 Ne从 40.5% 降至 31.6%。然而在其他条件相同的情况下，随着石子级配 (G) 的增大，透水混凝土的有效空隙率 Ne增大。例如，当固定水泥用量为 320kg/m3，水灰比从 0.25 增大到 0.35 时，石子级配为 2.36～4.75mm 的透水混凝土的有效空隙率 Ne从 34.8% 降至 28.0% 小于石子级配变为 9.5～16.0mm 的透水混凝土的有效空隙率 Ne从 35.4% 降至30.6%。这说明随着水灰比的增大，水泥浆体体积的增大，水泥浆体逐渐填充到石子空隙中去，使透水混凝土的有效空隙率 Ne减小；同时石子的级配越小，石子的空隙率越小，透水混凝土的有效空隙率 Ne也越小。不同石子级配 (G) 的情况下，水灰比 (W/C) 与水泥用量 (C) 对透水混凝土的有效空隙率 Ne的影响如下图 4、5 所示。

图 4 透水混凝土的有效空隙率 Ne等高线(石子级配 G：2.36～4.75mm)

图 5 透水混凝土的有效空隙率 Ne等高线(石子级配 G：9.5～16.0mm)

2.2.3 透水混凝土有效空隙率 Ne与空隙率 N0的关系

由上述 2.2.2 与 2.2.3 节的讨论，水灰比 (W/C) 与石子级配 (G) 对透水混凝土空隙率 N0与有效空隙率 Ne影响规律相似，揭示透水混凝土空隙率 N0与有效空隙率 Ne同样存在某种关系。混凝土中的空隙包括连通空隙、半连通空隙及封闭空隙，而有效空隙包括连通空隙和半连通空隙[5]。因此，透水混凝土有效空隙率 Ne与空隙率 N0存在线性相关。图 6 所示，透水混凝土有效空隙率 Ne与空隙率 N0存在很高的线性正相关，表明透水混凝土的空隙率 N0越大，有效空隙率 Ne也越大。

图 6 透水混凝土空隙率 N0与有效空隙率 Ne的相关性

2.2.4 透水混凝土的透水系数 K

由表 5 可知，透水混凝土的透水系数 K 大小显著受水灰比 (W/C)、石子级配 (G) 的影响；由公式 (8) 可知，影响透水混凝土的透水系数 K 大小顺序为：水灰比 (W/C)＞石子级配(G)(-2.03∶0.72)，石子级配 (G) 对透水混凝土的有效空隙率 Ne大小的贡献比水灰比 (W/C) 小约 65%。从图 7、8 可看出，在其他条件相同的情况下，随着水灰比 (W/C) 的增大，透水混凝土的透水系数 K 减小。例如，当石子级配固定为 2.36～4.75mm，水泥用量为 320kg/m3，水灰比从 0.25 增大到 0.35 时，透水混凝土的透水系数 K 从 18.60mm/s 降至14.23mm/s；同样当石子级配固定为 9.5～16.0mm，透水混凝土的透水系数 K 从 19.63mm/s 降至 15.52mm/s。然而在其他条件相同的情况下，随着石子级配 (G) 的增大，透水混凝土的透水系数 K 增大。例如，当固定水泥用量为 340kg/m3，水灰比从 0.25 增大到 0.35 时，石子级配为 2.36～4.75mm 的透水混凝土的透水系数 K 从 18.25mm/s 降至 14.28mm/s 小于石子级配变为 9.5～16.0mm 的透水混凝土的透水系数 K 从19.87mm/s 降至 16.05mm/s。这说明随着水灰比的增大，水泥浆体体积的增大，水泥浆体逐渐填充到石子空隙中去，使透水混凝土的透水系数 K 减小；同时石子的级配越小，石子的空隙率越小，透水混凝土的透水系数 K 也越小。不同石子级配 (G) 的情况下，水灰比 (W/C) 与水泥用量 (C) 对透水混凝土的透水系数 K 的影响如下图 7、8 所示。

图 7 透水混凝土的透水系数 K 等高线(石子级配 G：2.36～4.75mm)

图 8 透水混凝土的透水系数 K 等高线(石子级配 G：9.5～16.0mm)

2.2.5 透水系数 K 与有效空隙率 Ne的关系

由上述 2.2.2 与 2.2.4 节的讨论，水灰比 (W/C) 与石子级配 (G) 对透水混凝土透水系数 K 与有效空隙率 Ne影响规律相似，揭示透水混凝土透水系数 K 与有效空隙率 Ne同样存在某种关系。有效空隙包括连通空隙和半连通空隙，而有效空隙是能够通过水、排出水的空隙[5]。因此，透水混凝土透水系数K 与有效空隙率 Ne存在线性相关。图 9 所示，透水混凝土透水系数 K 与有效空隙率 Ne存在很高的线性正相关，表明透水混凝土的有效空隙率 Ne越大，透水系数 K 也越大。

图 9 透水混凝土有效空隙率 Ne与透水系数 K 的相关性

2.2.6 透水混凝土的抗压强度(f7d，f28d)

由表 5 可知，透水混凝土的抗压强度 (f7d，f28d) 大小显著受石子级配 (G)、水泥用量 (C) 的影响；由公式 (9)、(10) 可知，影响透水混凝土的抗压强度 (f7d，f28d) 大小顺序为：水泥用量(C)＞石子级配(G)，石子级配 (G) 对透水混凝土的抗压强度 (f7d，f28d) 大小的贡献比水泥用量 (C) 小约 5%～8%。图10、11 不同石子级配下，透水混凝土的 7d 抗压强度等高线；图 12、13 不同石子级配下，透水混凝土的 7d 抗压强度等高线。

从图 10～12 中可以看出，在其他条件相同的情况下，水泥用量越多，透水混凝土抗压强度越高，这一结论与普通混凝土相同。而石子级配不同，透水混凝土的强度变化规律不同。在其他条件相同的情况下，石子级配为 2.36～4.75mm配制的透水混凝土强度明显高于 9.5～16.0mm 的。因此，在其他条件相同的情况下，石子级配为 2.36～4.75mm 配制的透水混凝土空隙率 N0、有效空隙率 Ne及透水系数 K 小于9.5～16.0mm 配制的透水混凝土的(比较图 2、3，图 4、5，图 7、8)，但石子级配为 2.36～4.75mm 配制的透水混凝土结构比 9.5～16.0mm 配制的透水混凝土紧密，抗压强度 (f7d，f28d) 高于 9.5～16.0mm 配制的透水混凝土(比较图 10、11，比较图 12、13)。

图 10 透水混凝土的 7d 抗压强度等高线(石子级配 G：2.36～4.75mm)

图 11 透水混凝土的 7d 抗压强度等高线(石子级配 G：9.5～16.0mm)

图 12 透水混凝土的 28d 抗压强度等高线(石子级配 G：2.36～4.75mm)

图 13 透水混凝土的 28d 抗压强度等高线(石子级配 G：9.5～16.0mm)

2.3 优化试验方案

在试验结果分析及模型拟合的基础上，利用软件 Design-Expert 进行试验优化，在满足透水系数 K、抗压强度 (f7d，f28d) 最大，水泥用量 (C) 最少的情况下，得到两种不同石子级配 (G) 的最佳配合比方案，具体数据见表 6。

表 6 两种不同石子级配 (G) 的最佳配合比方案

3 结论

本论文采用两水平（最大值和最小值）的析因设计的试验方案能较好的模拟各透水混凝土因子（水灰比、骨料级配、水泥用量）对透水混凝土的空隙率、有效孔隙率、透水系数及抗压强度的影响。现将上述讨论所得结论陈述如下：

（1）在其他条件相同的情况下：随着水灰比 (W/C) 的增大，透水混凝土的空隙率 N0、有效空隙率 Ne及透水系数 K减小；随着石子级配 (G) 的增大，透水混凝土的空隙率 N0、有效空隙率 Ne及透水系数 K 增大，但抗压强度 (f7d，f28d) 减小；水泥用量 (C) 越多，透水混凝土抗压强度越高。

（2）透水混凝土有效空隙率 Ne与空隙率 N0之间、透水系数 K 与有效空隙率 Ne之间存在很高的线性正相关。

（3）利用软件 Design-Expert 进行试验优化，得出满足透水系数 K、抗压强度 (f7d，f28d) 最大及水泥用量 (C) 最少的情况下，得到两种不同石子级配 (G) 的最佳配合比方案：水灰比 0.25，石子级配 2.36～4.75mm，水泥用量 330.54 kg/m3；水灰比 0.34，石子级配 9.5～16.0mm，水泥用量327.86kg/m3。

[1] Malhotra V M．Advances in concrete technology[J]． Construction and Building Materials，1993,7(3):187．

[2] Nader G.，Shivaji D.．Development of no-fines concrete pavement applications[J]．Journal of Transportation Engineering，1995,121(3):283-288．

[3] Sonebi M., Bassuoni M T.．Investigating the effect of mixture design parameters on pervious concrete by statistical modeling[J]. Construction and Building Materials ，2013,38:147-154．

[4] 徐仁崇，刘君秀，曾冲盛，蔡振哲．采用 Design-Expert 软件优化透水混凝土配合比设计[J]．新型建筑材料，2010,7:17-20.

[5] 郑木莲．多孔混凝土排水基层研究[D]．西安:长安大学，2004.

[6] 张巨松，张添华，宋东升，等．影响透水混凝土强度的因素探讨[J]．沈阳建筑大学学报(自然科学版)，2006(5):759-763.

[7] Douglas C. Montgomery 著傅珏生，张健，王振羽，解燕译．试验设计与分析(第6版)[M]．人民邮电出版社，2009.

［通讯地址］江苏省南通市海安经济开发区花园大道 88 号南通众润混凝土有限公司（226600）

An application of numerical modeling on effect of performance of pervious concrete research

Wei Yong, Zuo Wenluan, Zhang Hongming , Fan Jianfeng
(Recycling Technology Development Center of Nantong Zhongrun Concrete Co.,Ltd, Jiangsu 226600,China )

In this paper, two-level factorial design and response surface methodology (RSM) were used, to study the effects of waterto-cement ratio (W/C), aggregate gradation (G) and cement content (C) on void ratio N0, effective porosity Ne, permeation coefficient K and compressive strength (f7d，f28d) of pervious concrete, and established the corresponding mathematical models. The research results show that: with the increase of water-to-cement ratio (W/C), void ratio N0,effective porosity Neand permeation coefficient K of pervious concrete decreased under the same conditions. However, with the increase of aggregate gradation (G), void ratio N0, effective porosity Ne and permeation coefficient K of pervious concrete increased. The more cement content (C), the higher compressive strength (f7d，f28d) of pervious concrete. The models in this study can facilitate optimizing the mixture proportions of pervious concrete for target performance.

pervious concrete; two-level factorial design; response surface methodology; mix optimization

魏勇（1986— ），男，硕士，主要从事混凝土质量控制与材料综合利用工作。