基于缝端损伤区域的混凝土材料Ⅱ型裂缝扩展角研究

陈殿华，王向东，邵 兵

(河海大学力学与材料学院，江苏南京 210098)

由于混凝土是由水泥、砂、骨料、水等材料组成的复合材料，所以在实际工程中混凝土结构难免会出现裂缝。为了确保混凝土结构的安全，裂缝的稳定性分析和扩展规律的研究是工程界普遍关心的问题［1-2］。

实验表明，混凝土结构缝端存在微裂纹区，称为损伤区域。随着外界因素的作用，损伤区域不断演化发展，导致裂缝向损伤区域内扩展，因此裂缝缝端损伤场及变化规律与裂缝扩展密切相关［3-4］。目前，对于单一型裂缝的损伤方程、损伤场计算等研究成果较多［5-6］。对于Ⅰ型、Ⅱ型和Ⅲ型等单一型裂缝及Ⅰ～Ⅲ复合型裂缝的扩展角研究大多是基于断裂力学的方法［7-8］。根据损伤理论和断裂理论［9-10］的经典判据，包括应力强度因子判据、能量判据等，可以从损伤的角度来研究裂缝扩展角。Ⅱ型裂缝扩展角相对比较复杂，所以本文基于Ⅰ型裂缝的损伤方程，推导出更适用于Ⅱ型裂缝的损伤演化方程，研究缝端损伤场的发展规律，将Ⅱ型裂缝缝端的损伤梯度出现极值时对应的角度确定为Ⅱ型裂缝的扩展角，并将该扩展角与经典判据得到的扩展角进行对比，以验证该方法的可行性。

1 单一型裂缝三维空间内缝端应变间的关系

材料相同的两块带缝混凝土试件，分别在Ⅰ型裂缝和Ⅱ型裂缝损伤的受力情况下，对处于纯剪状态的Ⅱ型裂缝试件采用第二强度理论分析，对处于单轴应力状态的Ⅰ型裂缝试件采用第一强度理论分析，得

由式(1)得

式中:τxz——切应力;ν——混凝土的泊松比，ν∈(0.16，0.18)［11］;nτ——剪切安全因子;σ——混凝土材料的许用拉应力;nσ——受拉形式下的安全因子。

假设外荷载产生的拉应力σ1与τxz按一定的比例分别对两块混凝土试件加载，根据胡克定律、G=为剪切模量;E为弹性模量)和式(2)，得

式中:γxz——Ⅱ型裂缝切应变;ε1——Ⅰ型裂缝线应变。

2 建立Ⅱ型裂缝的损伤方程

Loland［12］在对混凝土等脆塑性材料的试验结果进行研究后发现，当应力将要达到峰值应力时，应力应变关系已经不再是线性关系，表明在达到最大应力之前，材料内部已经存在损伤，在峰值应力之后，裂缝周围材料的损伤积累并发展。

将裂缝混凝土单轴拉伸试验进行数据拟合可以得到损伤方程［13］:

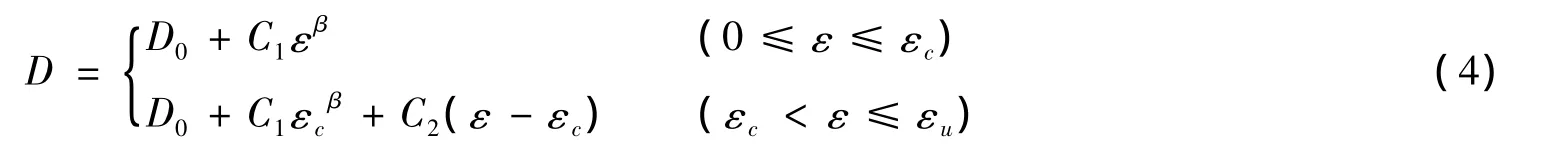
式中:D0——混凝土初始损伤;C1、C2、β——材料常数;εu、εc——极限拉应变、峰值拉应变。

根据式(3)和式(4)，可得适用于Ⅱ型裂缝用切应变表示的损伤方程:

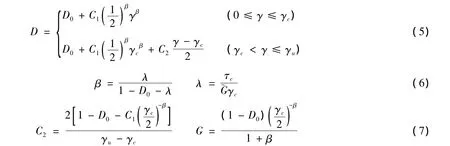
式中:γu、γc——极限切应变、峰值切应变。

根据G和E的关系，本文采用文献［14］中由E研究得到的D0=0.05和峰值损伤Dc=0.18，其他参数为τc=2.1 MPa，γc=2×10-4，γu=10-3，τu=2.6 MPa，G0=1.4×104MPa，~G=1.3×104MPa。

由式(6)(7)可以得到λ=0.75，β=4，C1=2×1015，C2=938。

将材料常数代入式(5)得

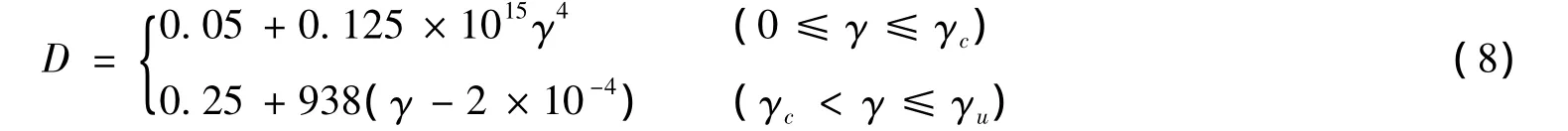
由式(8)得到结论:随着混凝土材料受损程度的不断变大，应变量逐渐变大。

3 混凝土Ⅱ型裂缝损伤区域分析

Ⅱ型裂缝尖端应力场公式为

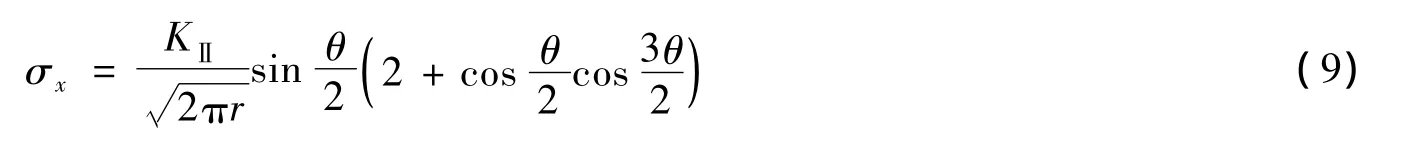
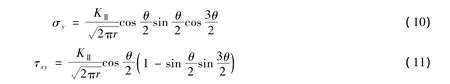
式中:r、θ——缝端极坐标;KⅡ——应力强度因子。定义缝端的微裂纹区为缝端损伤区，由式(9)(10)求出第一、第三主应力代入莫尔强度理论［11］，得到混凝土材料Ⅱ型裂缝试件裂缝尖端损伤区r的计算公式:

由式(12)得到Ⅱ型裂缝损伤演化规律如图1所示。

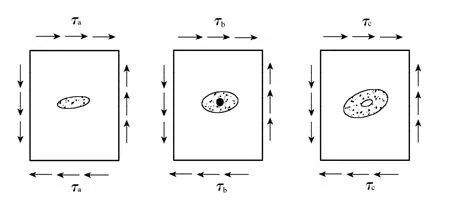
图1 Ⅱ型裂缝损伤演化示意图Fig.1 Damage evolution schema of modeⅡcrack

4 Ⅱ型裂缝损伤梯度及扩展角

4.1 计算

将τxy=G0(1-D)γxy带入式(9)～(11)，得，进行分析，得到缝尖损伤梯度的表达式为

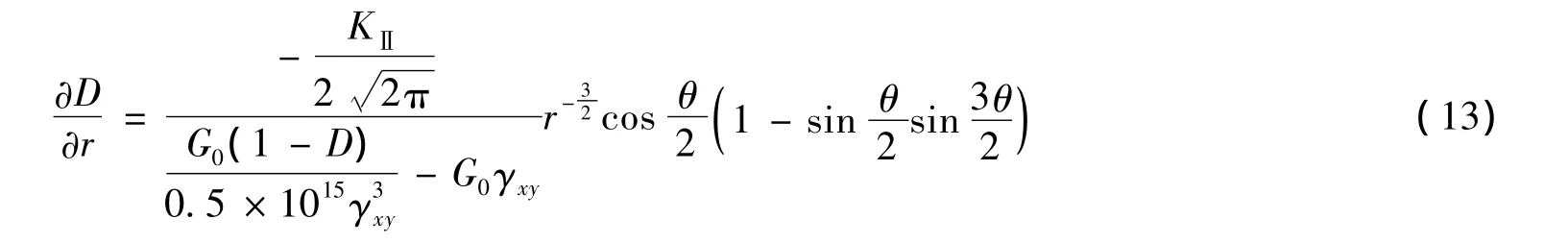
将式(12)带入式(13)，则缝尖损伤梯度与裂缝扩展角的关系可以表示为

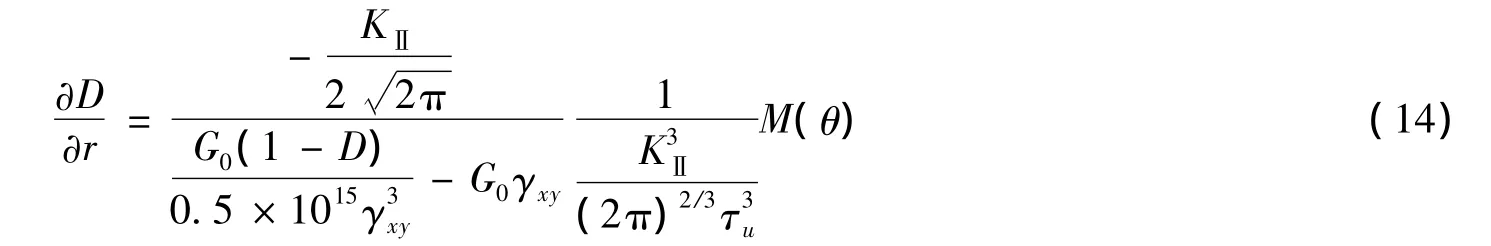
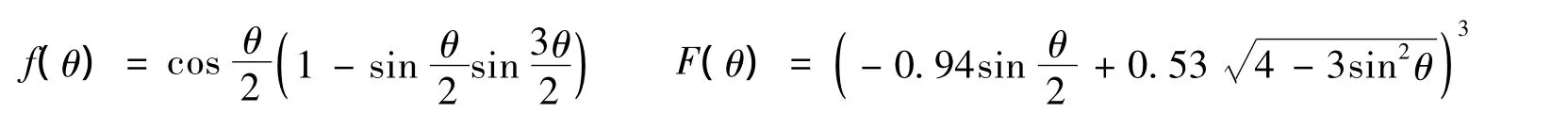
式中:τ——切向荷载在带缝混凝土表面产生的切应力。

裂缝的扩展是由于随着荷载的加大，材料所受的损伤也不断变大造成的，其扩展角必定是损伤梯度极大时对应的θ。由式(14)得到极大时，M(θ)必定出现极大值。通过软件计算，得到M(θ)～θ曲线图(图2)，最终得到M(θ)极大时对应的θ分别为:4°，16°，26°，29°，39°，43°，52°，65°，79°。

4.2 验证

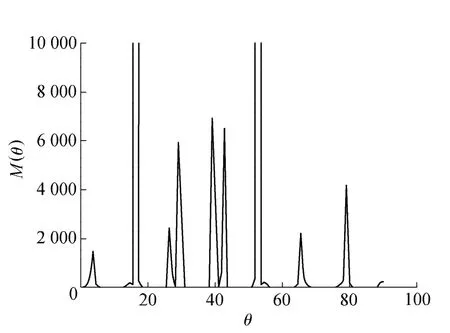
图2 M(θ)随扩展角θ变化的规律Fig.2 Variation of M(θ)with propagation angle θ

根据经典理论求得的Ⅱ型裂缝扩展角约为79.3°［15］，本文方法所求得的裂缝扩展角与经典理论所求得的扩展角误差为0.3%，验证了本文方法的正确性。

5 结 论

目前，对于裂缝扩展角的研究大多是基于断裂力学理论。本文从损伤角出发，由损伤梯度研究Ⅱ型裂缝扩展方向的变化规律，得到了裂缝扩展方向是按损伤梯度逐步增大的规律变化的结论，计算出Ⅱ型裂缝失稳扩展角为79°，该结论与经典理论求得的结果吻合很好，表明基于缝端损伤梯度研究裂缝扩展角的可行性。

［1］李军.混凝土Ⅰ-Ⅱ复合型断裂起裂准则的试验研究［D］.大连:大连理工大学，2008.

［2］刘梦和，王向东，邵兵.Ⅰ-Ⅱ复合型裂缝应力强度因子和应变能释放率的关系［J］.水利水电科技进展，2012，32(6): 31-33.(LIU Menghe，WANG Xiangdong，SHAO Bing.Relationship between stress intensity factor and strain energy release rate ofⅠ-Ⅱ mixed mode cracks［J］.Advances in Science and Technology of Water Resources，2012，32(6):31-33.(in Chinanese))

［3］逯静州.三轴受压混凝土损伤特性理论与试验研究［D］.大连:大连理工大学，2001.

［4］李敏.混凝土损伤研究［D］.河南:河南大学，2005.

［5］田佳琳，李庆斌.混凝土Ⅰ型裂缝的静力断裂损伤耦合分析［J］.水利学报，2007，38(2):205-210.(TIAN Jialin，LI Qingbin.Fracture-damage coupled analysis for modeⅠcracking in concrete under static load［J］.Journal of Hydraulic Engineering，2007，38(2):205-210.(in Chinanese))

［6］董伟.混凝土Ⅰ-Ⅱ复合型裂缝起裂准则的试验研究与裂缝扩展过程的数值模拟［D］.大连:大连理工大学，2007.

［7］CHOYYC K M.Anew mixed mode fracture criterion:maximum tangential strain energy density criterion［J］.EnginFract Mech. 1991，39(3):433-449.

［8］邵兵，王向东，刘梦和.空间复合型裂纹的性能参数［J］.水利水电科技进展，2012，32(5):53-54.(SHAO Bing，WANG Xiangdong，LIU Menghe.Study on performance parameters of spatial mixed mode crack［J］.Advances in Science and Technology of Water Resources，2012，32(5):53-54.(in Chinanese))

［9］HEOS P，YANG W H.Mixed-mode stress in tensity factors and critical angles of cracks in bolted joints by weight functionmethod［J］.Archiveof AppliedMechanics，2002，72(2):96-106.

［10］KRISHNANG R，ZHAO X L，ZAMAN M，et al.Fracture toughnessof asoft sandstone［J］.International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts，1998，35(6):695-710.

［11］徐道远，黄孟生，朱为玄，等.材料力学［M］.南京:河海大学出版社，2004:6，29.

［12］LOLAND K E.Continuum damage model for load response estimation of concrete［J］.Cement and Concrete Research，1980，10，395-402.

［13］余天庆，钱济成.损伤理论及其应用［M］.北京:国防工业出版社，1998:138-140.

［14］朱岳明，徐之青，贺金仁，等.混凝土水管冷却温度场的计算方法［J］.长江科学院院报，2003，20(2):19-22.(ZHU Yueming，XU Zhiqing，HE Jinren，et al.A calculation method for solving temperature field of mass concrete with cooling pipes［J］.Journal of Yangtze River Scientific Research Institute，2003，20(2):19-22.(in Chinanese))

［15］郦正能，何庆芝.工程断裂力学［M］.北京:北京航空航天大学出版社，1993:110-113.