分数傅立叶变换核函数的分析与重构*
2014-03-13张静
张静
(黑龙江建筑职业技术学院)
0 引言
经典傅立叶变换的发展使一类分数傅立叶变换应用得到广泛的推广,当然这是由于分数傅立叶变换具有自己特殊的优势,它具有时频分析的性质,这种分数傅立叶变换具有的性质,能很好的促使这种变换得到越来越多的应用[1-2]. 2003~2006年,冉启文研究了分数傅立叶变换的多样性,通过他的努力,使他得到重大的理论突破,那就是以算子周期性为主要特色和着眼点的分数傅立叶变换多样性的结论,这个结论对于傅立叶变换是个很优美的结论[3].该文从采样出发研究分数傅立叶变换多样性.
1 对采样的分析
研究中,对采样可以选定一个由特征函数可以构成的基,如{φn(t)|n∈N}和一个GS,如gn,n∈N,这样就可以构造出如下相应的FRFT核函数
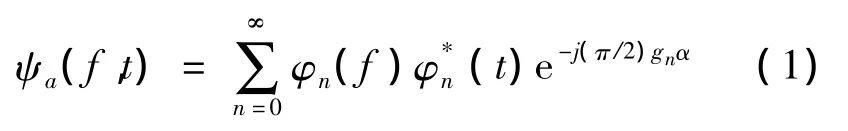
简化(1)式中的核函数有
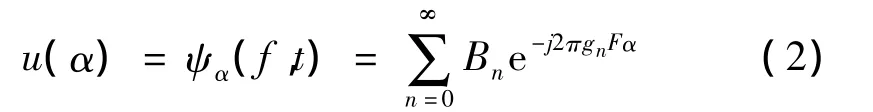
在式(2)中,可以看到:其中Bn=φn(f)φ*n(t),而且f和t是固定不会改变的.为了表述得更清楚,可以用Tp来表示u(α)一般周期的形式,而在这里F表示一般的频率,请注意式中的Tp=4和F=1/4.同时,对于周期“信号”公式(2)也可以用傅立叶级数的形式表示,如下式
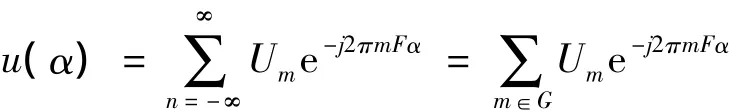
Nm是空集时,Um=0,即m∉G.注意:系数Bn独立于GS gn,否则,傅立叶系数Um依赖于gn.
定理1.1 对于信号u(α)来说,如果它是周期为Tp的周期信号,那么它就会具有有限谐波的支撑σ(u),C是一个大小为N的单位元,它会包含着σ(u),可以用C⊃σ(u)表示,那么,对于这个信号就可以利用N个采样u(nT)来表示,T=Tp/N,可以根据下述公式进行完美的重构
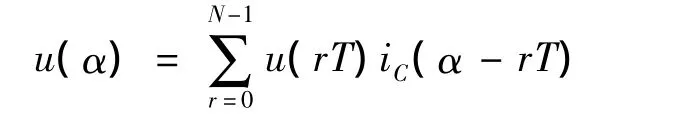
对于核函数的采样重构的进行,实际上是求解线性方程组的推导演算过程.它的核函数可以用下式表示
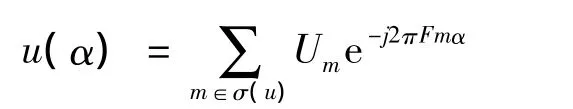
设在一个周期内的采样点分别为:α1,α2,…,αn,则得到以下矩阵

将Um表示为u(α)的某些点上的值,可以与一定的插值函数得到组合形式来进行表示,在这个表示式中,其中m1,m2,…,mN∈σ(u)的表示形式,就是采样重构.
传统采样的点是利用函数u(α)来表示,这是在一个周期内的等间隔采样方式,在这种表示形式中,对于σ(u)是利用它的最小单位元C所代替,对于这个单位元C,它是由N个模,而且对于N是由互不同余的数组成,所以得到的变换矩阵,就可以利用如下的形式表示:

其中W=e-j2π/N,T=Tp/N.N=|C|.
事实上,当谐波支撑刚好是单位元,这时的N点采样是最有效率的.
2 核函数的重构
通常情况下,用最小单位元C代替支撑集σ(u),则有核函数
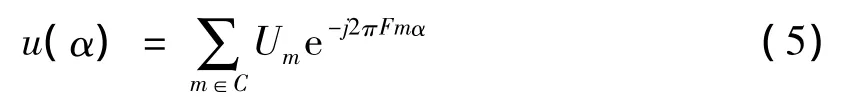
设采样点分别为α1,α2,…,αn,C是一个大小为N的包含σ(u)的最小单位元,则得到如下形式

其中m1,m2,…,mN∈C.
对任意T1,满足0<T1≤Tp,设T1/Tp=l,0<l≤1,在[0,T1]上进行N个等间隔采样,T=T1/N为采样间隔,则核函数采样有如下形式
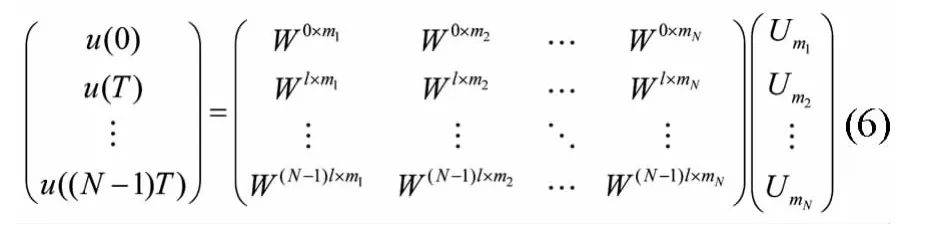
其中m1,m2,…,mN∈C,W=e-j2π/N
令Wl×m1=ti,i=1,2,…,N,则(6)中的矩阵记为M,则有

因为t1,t2,…,tN互不相同,所以矩阵|M|≠0,矩阵M可逆.
设f(x)=c0+c1x+…+cN-1xN-1,将t1,t2,…,tN分别代入并整理得
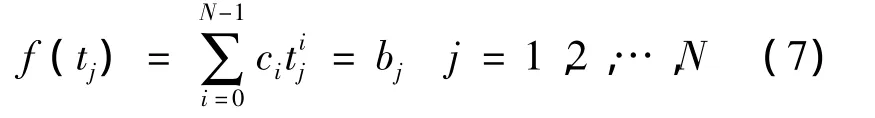
即(c0,c1,…,cN-1)T是如下方程组
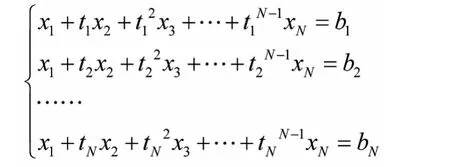
的解向量.此线性方程组的系数矩阵是N阶Vandermonde矩阵[4],记为A

因为矩阵|A|≠0的原因,所以对于矩阵A来说是可逆的,从而对于线性方程组(7)来说,只有唯一的解.
令C=(c0,c1,…,cN-1)T,
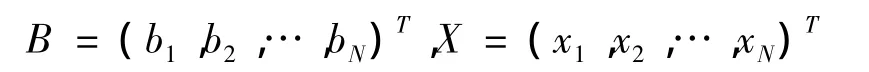
则向量C是线性方程组AX=B的唯一解,所以C=A-1B,而
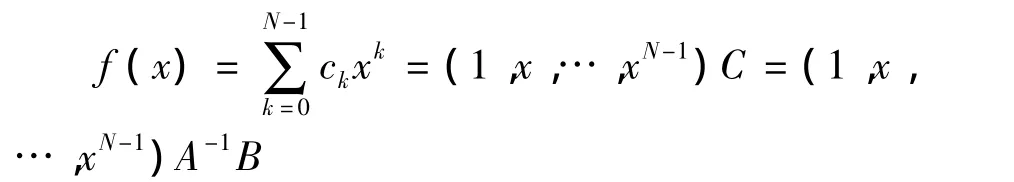
在上式中,设

记矩阵A的伴随矩阵为A*=[Ai,j]1≤i,j≤N,则
A-1=,于是有

对于(9)式,可以将矩阵A的第j行改写成如下形式,既(1,x,…,xN-1),而对于其余的元素,都保持着不变的形式,此时,对于所得的矩阵,可以记为Aj.这样就可以根据行列式,得到展开的Laplace定理,矩阵Aj的行列式,可以用下式表示,既为
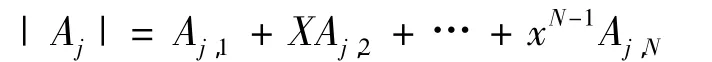
则(9)式可写成如下形式
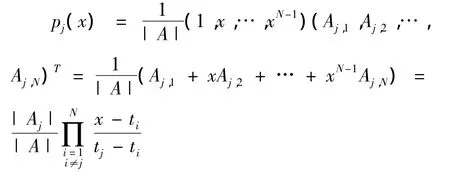
整理得
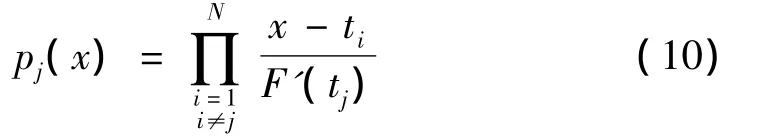
利用(8)式可以求得Vandermonde矩阵A的逆矩阵A-1[5].
若用σr(x1,x2,…,xm)=表示字母x1,x2,…,xm的r次初等对称多项式,r=1,2,…,m,σ0(x1,x2,…,xm)=1,利用初等对称多项式和式(10)则有(j=1,2,…,N)
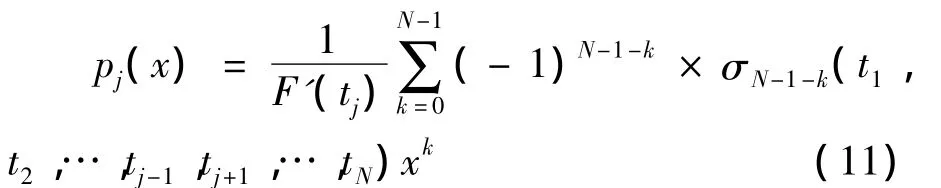
记矩阵A的逆矩阵为A-1=[ai,j]1≤i,j≤N,由(8)式可知

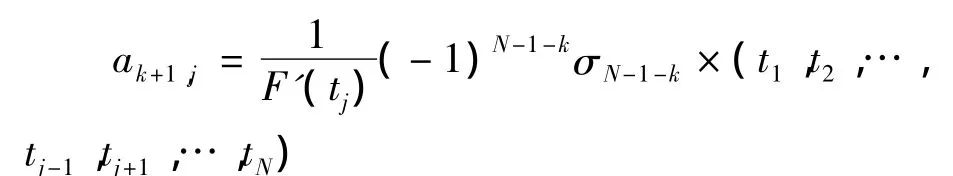
从而A-1的第i行第j列的元素ai,j是
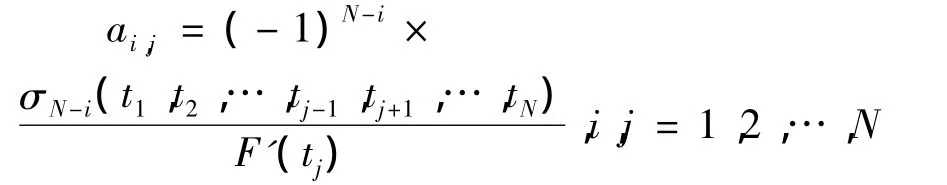
很明显,矩阵M=AT,从而可知M-1=(A-1)T.由(6)式可得

将Umi代入(5)式有
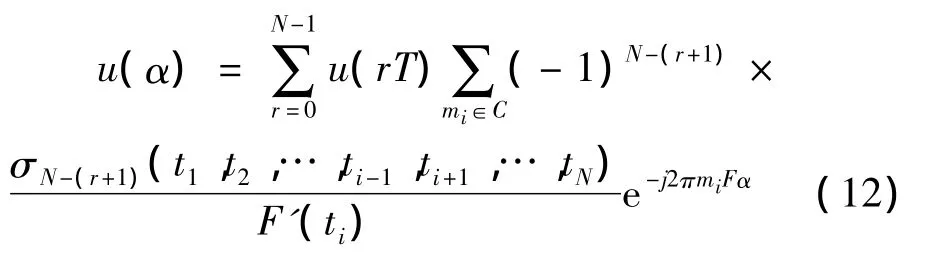
此公式即是核函数的重构公式.其系数为
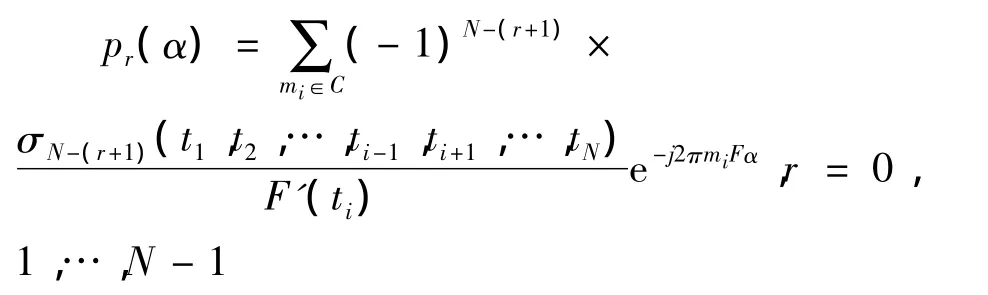
其中ti=Wl×m1,i=1,2,…N,W=e-j2π/N,m1,m2,…,mN∈C.
当l=1时,利用上述方法得到核函数重构公式的表示式实际上就是定理1.1中的重构公式.利用这种方法与定理1.1中的方法相比,就可以发现更具有一般性,显然,这对于分数傅立叶变换多样性研究的应用范围,提供了一种更为有效的工具,有利于科学的发展.
对于重构系数之间,它们是存在一定相关性的.当N=4,C={0,1,2,3},l=1/2时,就可以直接计算得到下式:p(α)=p0(α)+p1(α)+ p2(α)+p3(α)=1.
除此之外,系数之间呈现“共轭对”关系,即p0(α)=(α),p1(α)=(α).
为了加深对这些系数的理解,图1给出了系数仿真的图像,其中l=1/2.
从图1可以看出,系数曲线完成的圈数与单位元中的最大值,从仿真的图像可以看到,它们具有一定的相关性的,这种相关性可以描述为,单位元中的最大值越大,图像转的圈数就越多,对于仿真的图像的理论证明有待于进一步的研究结果.
事实上,当N=4n,n=1,2,3,…,C={0,1,2,…,N-1},对任意(0,1]区间上的实数l,下式都成立:
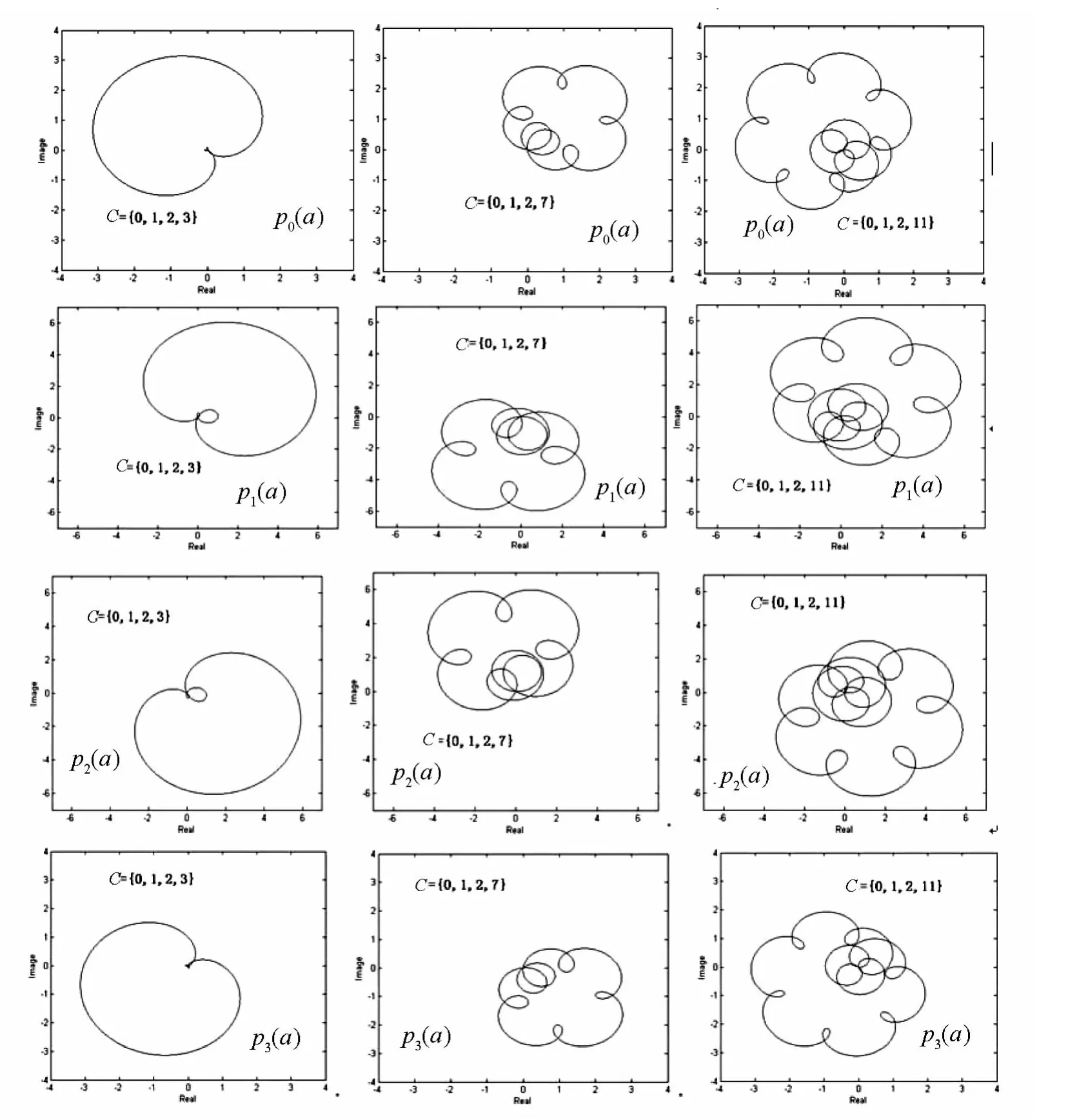
图1 单位元大小为4的系数p0(α)、p1(α)、p2(α)、p3(α)的图像
p(α)=p0(α)+p1(α)+…+pN-1(α)=1且系数之间仍然有“共轭对”关系 pi(α)=),i=0,1,…,4n-1.
并且图像转的圈数与单位元中的最大值也有上述的关系.
3 结束语
通过利用特殊Vandermonde矩阵的逆矩阵的探讨,可以证明对任意有限带宽的周期信号的处理,它们都可在[0,T1],0<T1≤Tp上进行等间隔的采样,并且可以得到重构,这样就可以得到核函数的重构公式.然后通过分析重构公式中系数的关系,得到经典的结果.该文的研究方法,为分数傅立叶变换多样性之间关系研究,开辟了一种有利的工具,利用这种研究途径,可以研究在任意区间[0,T1]上的非等间隔采样的模式,这样就可以将信号得到重构,具体的应用方法,将在以后的工作中继续研究.关于核函数的采样,这是基于对信号在分数傅立叶变换下,可以得到的进行各种性质研究的基础和前提,如果再考虑分数傅立叶变换多样性的影响,可以相信,一定会具有重大的理论发展前景和实际的指导意义.
[1] Pei SC,Yeh M H,Luo T L.Fractional Fourier Series Expansion for Finite Signaland Dual Extension to Discrete-time Fractional Fourier Transform.IEEE Trans Signal Processing,1999,47(10):2883-2888.
[2] Pei SC,Ding J J.Closed-form Discrete Fractional and Affine Fourier Transforms.IEEE Trans Signal Processing,2000,48(5):1338-1353.
[3] Ran QW,Yeung D S,Tsang C C,et al.General Multifractional Fourier Transform Method Based on the Generalized Permutation Matrix Group.IEEE Trans Signal Processing,2005,53(1):83-98.
[4] 杨胜良,乔占科.Vandermonde矩阵的逆矩阵的一种显示算法[J].兰州理工大学学报,2004,30(6):131-133.
[5] 谭畅,季春玉,龚俊松,等.基于Canny算子的有效块匹配运动估计算法[J].哈尔滨商业大学学报:自然科学版,2012(1):92-94.
