大型疏绕螺线圈组磁场的仿真与测试

黄刘宏，李跃波，杨 杰，丁世敬，刘 锋

(总参工程兵科研3 所 第4 研究室，河南 洛阳 471023)

低频强磁场模拟器是采用高压高能脉冲源对大型螺线圈放电方法，在螺线圈内部产生脉冲强磁场。通过对回路脉冲激励电流波形的控制，可模拟地面核爆炸产生的特定幅值和上升时间的磁场，进而为低频脉冲强磁场的破坏效应及防护技术研究提供了性能先进的试验手段。

低频强磁场发生线圈作为整个模拟器系统的核心设备之一，其为一大型螺线圈组:是由相同尺寸、均匀间隔25 cm 的4 个螺线圈组成，每个螺线圈均由直径10 mm，壁厚1 mm 的紫铜管以1 匝/m 绕制成直径6 m，长度10 m 的空间螺旋线状。螺线圈组实物照片如图1 所示。该线圈组产生的磁感应强度及内部空间磁场分布的均匀性是整个模拟器研制的重要指标，但由于线圈组是由4 个平行套接的螺线圈组成，且每个线圈均为疏绕螺线圈，因此整个线圈组产生的磁场无法利用现有适用于单个螺线圈的磁场公式进行计算［1－3］。为解决上述问题，本文利用Ansys 仿真对实体线圈组的磁场及其均匀性进行了计算和分析，并结合试验测试进行了验证，研究结论为本系统磁场模拟器相关指标的确定提供了直接依据。

1 仿真分析

由于对同一线圈而言，其在空间某点处产生的磁场与激励电流成线性关系，因此在分析螺线圈组产生的磁场幅值时，可采用稳恒电流激励，而非实体线圈中的脉冲激励电流形式。这样可将瞬态电磁场问题转换为静磁场问题，从而大幅减少了仿真计算量，并缩短了计算时间。

Ansys 仿真时采用Solid 96 单元进行静磁场分析，源电流采用Source 36 虚单元［4］。在建立空间螺线圈几何模型时采用分段圆弧的方式，即单匝线圈设定由数个圆弧段组成，经多次试算，在综合考虑计算精度和效率后设定为20。考虑到螺线圈模型的对称性，为减小计算量提高计算效率，计算模型为全模型的1/4。近场区和远场区采用不同的网格划分尺寸，以兼顾计算精度和效率。经多次试算与比较，设定近场区内网格尺寸为150 mm，远场区网格尺寸为800 mm。图2为近远场设置和1/4 计算域网格剖分图。图3 为仿真计算的磁感应强度矢量分布图及幅值云图。Ansys 仿真时设定4 个螺线圈为并联激励，每个螺线圈中电流I=104/4 A。

图1 磁场发生线圈实物照片

图2 Ansys 4 个螺线圈计算模型

图3 Ansys 仿真计算的螺线圈磁感应强度

为了能与Ansys 仿真结果进行比较，这里将螺距1 m/匝，匝数10 的4 个螺线圈近似等效为螺距0.25 m/匝，匝数40 的单个螺线圈，并采用适用于单个疏绕螺线圈磁场的理论公式进行计算［5－6］，两者结果的对比如图4(a)和图4(b)所示。采样点分别为x0=(0，2.4，4.5，6)m，y0=0 m 处的轴向磁场分量Bz和径向磁场分量幅值。可看出Ansys 仿真结果与理论计算值基本吻合，只是局部存在差异，这种差异一方面来源于数值计算误差，另一方面则在于仿真采用的是与实体线圈一致的4 个螺线圈组模型，而理论计算将其等效为一个连续的单螺线圈模型。

从螺线圈内部磁场的峰值来看，在总电流为104A，4 个螺线圈连接方式为并联相加时，螺线圈组中轴线中心磁感应强度可达0.010 7 T，若4 个螺线圈为串联相加，则每个螺线圈中的电流均为104A，磁场幅值可达0.04 T。上述指标均满足系统设计要求。

图4(c)为螺线圈中间位置半径平面内的Bz峰值曲线。需指出的是，Ansys 仿真虽能够给出理论公式，却不能计算螺线圈所在位置处的磁感应强度。根据图4(a)和图4(c)中轴向磁场分量Bz的数值能进一步确定:在螺线圈中心位置处3.6 m×3.6 m×3.6 m的空间内，均可满足系统设计均匀性＜10%的要求。

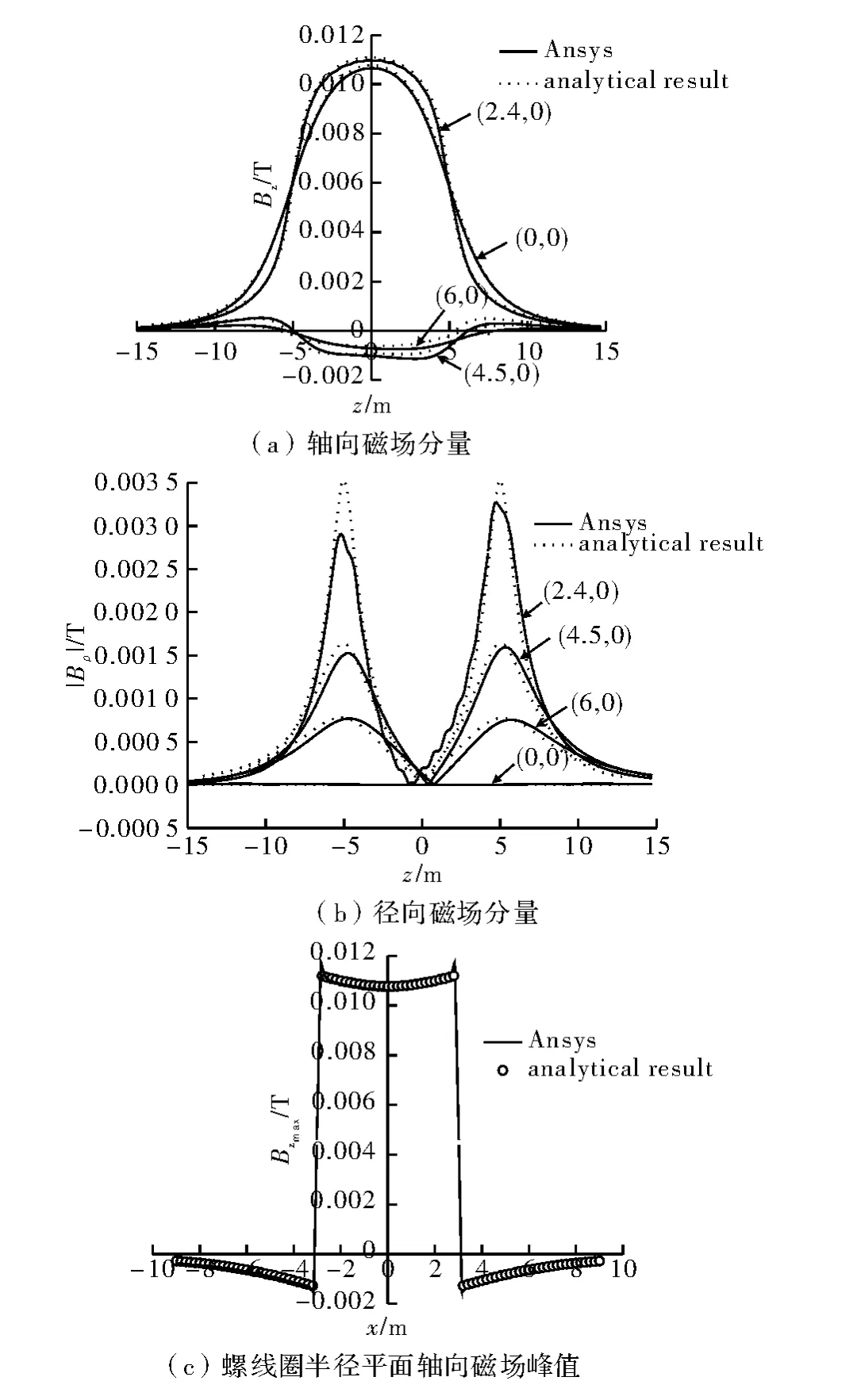
图4 Ansys 仿真结果与理论结果的对比

2 试验测试

为测试螺线圈内部磁感应强度分布，购置了磁场测试系统。该测试系统基于电磁感应法，即在被测磁场区域放置小的探测线圈，外部磁场的变化导致探测线圈磁通量的变化进而产生感应电动势，通过建立的感应电动势与外部磁场的关系测得磁感应强度。该系统主要由GC1W－B 光发射机和GY100－1006 光接收机组成。光发射机上装有探测线圈，并将测得的电信号转换为光信号，通过光纤引出螺线圈所在的电磁屏蔽室。光接收机接收光纤导入的光信号并将其转换为电信号，再将其导入示波器即可实现被测信号幅值和波形的显示与测量。

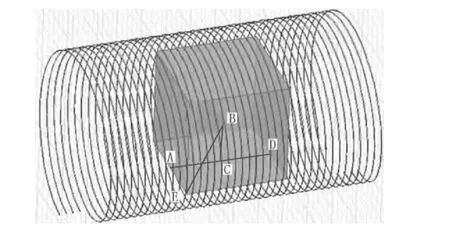
图5 磁场均匀度测点布置图

图6 磁场均匀度测试现场照片

按图5 所示布置5 个磁场传感器，测试现场照片如图6 所示。测点B 为螺线圈组中轴线的中心点，测点C 沿径向方向距测点B 1.8 m，测点A 和D 均沿轴线方向距测点C 1.8 m，测点E 距测点A 1.8 m。表1中在计算磁场均匀性时，以5 个测点值的平均值为基准，计算各点与平均值的最大偏差和最小偏差，二者差值的绝对值为均匀性数值。可看出，5 个测点处的均匀性值最大为9.1%，因此依据磁感应强度分布的轴对称性可知，在螺线圈组中间位置的3.6 m×3.6 m×3.6 m 方形区域内均可满足＜10%的均匀性指标要求，与仿真分析结果一致。

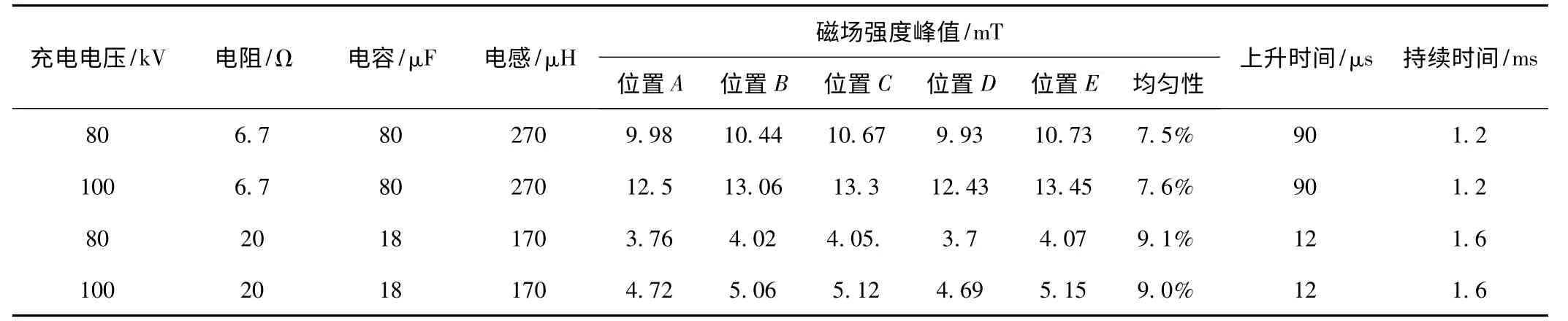
表1 磁场均匀性测试结果

3 结束语

(1)利用Ansys 对低频强磁场模拟试验设备中的磁场发生线圈组进行了仿真计算，在总电流为104A且4 个螺线圈连接方式为并联相加时，螺线圈组中轴线中心磁感应强度为0.01 T，若连接方式改为串联相加，则幅值可达0.04 T。上述指标均满足设计要求。同时将Ansys 仿真结果与疏绕螺线圈理论公式计算结果进行了对比，验证了仿真结果的正确性。

(2)仿真结果表明，在螺线圈组中心位置处3.6 m×3.6 m×3.6 m 的空间内，磁感应强度的均匀性＜10%。该区域可作为满足系统均匀性指标要求的磁场受试区。

(3)对于几何尺寸和连接方式确定的螺线圈模型，空间固定点处的磁感应强度幅值仅与激励电流的大小有关，因此尽管本文仿真计算时采用稳恒电流激励，但其结果对于实际线圈中为脉冲电流激励的情形也同样适用。

［1］ 雷照银.轴对称线圈磁场计算［M］.北京:中国计量出版社，1991.

［2］ 马文蔚.物理学:中册［M］.4 版.北京:高等教育出版社，1999.

［3］ BHAG S G.电磁场与电磁波:英文版［M］.北京:机械工业出版社，2002.

［4］ 张倩，胡仁喜，康士廷，等.ANSYS 12.0 电磁学有限元分析从入门到精通［M］.北京:机械工业出版社，2010.

［5］ 冯旺军.考虑螺距时圆截面螺线管电流磁场的空间分布［J］.桂林电子工业学院学报，2005，24(4):13－16.

［6］ 冯旺军.疏松型螺线管电流轴线上磁场的数值计算［J］.大学物理，2002，21(3):31－33.