内置中心支板的RBCC变几何二元进气道设计与数值模拟①

张 浩，李光熙，李 江，秦 飞，何国强

(1.西北工业大学 燃烧、热结构与内流场重点实验室，西安 710072;2.西安航天动力研究所，西安 710100)

0 引言

支板式火箭基组合循环［1－2］(Rocket Based Combined Cycle，简称RBCC)发动机利用流道中内置的中心主支板，将火箭发动机、燃料喷注模块、火焰稳定器集成于一体，具有性能优异、结构简单，重量轻，可靠性高等优点，已成为当今RBCC研究的一大热点。RBCC发动机具有飞行包线较宽的特点，即飞行马赫数范围和空域都很宽广。RBCC发动机可工作于引射、亚燃、超燃和纯火箭等4个模态，飞行马赫数可从零到十几马赫，飞行高度可覆盖从地面到大气层外的整个空域。为了保证RBCC发动机高效、稳定地工作，必须设计出与之相匹配的进气道。

RBCC发动机所采用的进气道包括轴对称、矩形截面(如二元混压或三维侧压)等形式。而无论何种形式的RBCC进气道，在低马赫数下都会遭遇不起动问题，其本质是进气道捕获的空气流量与进气道喉道所能通过的空气流量不匹配。引射模态下，为使RBCC发动机获得明显推力增益，需要有足够的进气量，进气道喉道面积要尽可能大。此外，不同来流马赫数下，进气道对来流空气的压缩程度要求是不同的。例如，高马赫数下，为了降低进气道出口气流马赫数，并提高增压比，需对来流有更大的压缩程度［3］，即需要更大的总收缩比。综上所述，为了降低进气道的起动马赫数，并使进气道在不同马赫数范围内均具有较优的性能，众多RBCC进气道采用了变几何方案。例如，美国的GTX［4］发动机进气道采用前后移动中心锥体位置的方法来调节进气道的收缩比;美国Aerojet公司的Strutjet［5］发动机采用侧压式进气道，通过调节进气道顶压板和燃烧室顶板位置，来改变不同马赫数下对来流空气的压缩程度。

目前，国内关于双模态超燃冲压发动机进气道的研究较多［6－7］，这类进气道起动马赫数往往较高(如常见的起动马赫数为3.5～4)，而具有更宽工作马赫数范围的RBCC进气道的详细公开文献报道［8］相对较少。本文以使用RBCC发动机作为第一级动力的两级入轨飞行器作为应用背景(飞行器拟从地面零速起飞，经引射、亚燃和超燃模态加速至Ma=7，第一级与第二级分离后返航，第二级继续加速攀升至大气层外入轨)，考虑到变几何结构的易于实现性，提出了一种内置中心支板的RBCC变几何二元混压式进气道方案。工作马赫数区间为0～7，起动马赫数不高于2.5。

1 RBCC变几何进气道模型

本文中进气道采用内置中心支板的可变几何二元混压形式，如图1所示。考虑飞行器的弹道为爬升型，设计点取为Ma=5，变几何后自起动马赫数为2.4。进气道前体采用三级外压缩，根据等强度激波理论进行设计，优化后的各级转折角分别为 5.5°/6.2°/7°，总转折角18.7°。设计点下三道外斜激波交于唇口，唇口内表面保持水平(可降低高马赫数下的唇口外罩阻力，同时避免进气道在设计点马赫数以上工作时，前体斜激波系交汇于唇口内侧可能诱发的局部正激波)。前体第三级外压缩面与喉道等直段底面采用圆弧过渡。进气道宽度150 mm，设计点捕获高度400 mm，隔离段出口高度100 mm。在内压缩通道中段，设置4个吸除槽［9］，可在较宽马赫数范围内，吸除唇口激波－附面层相互作用所形成流动分离区内的低速气体，改善进气道的起动性能［10］。设计点下进气道喉道等直段高度56 mm，长度为2倍高度。进气道总面积收缩比5.71，内收缩比 1.98。隔离段呈单侧扩张形，扩张角 4.6°，隔离段后半段内置中心支板，支板半楔角3.5°，中心支板等宽处的宽度45 mm(即中心支板占空比0.3)。通过上述设计，可保证在整个工作马赫数范围内进气道的几何喉面均位于喉道等直段。

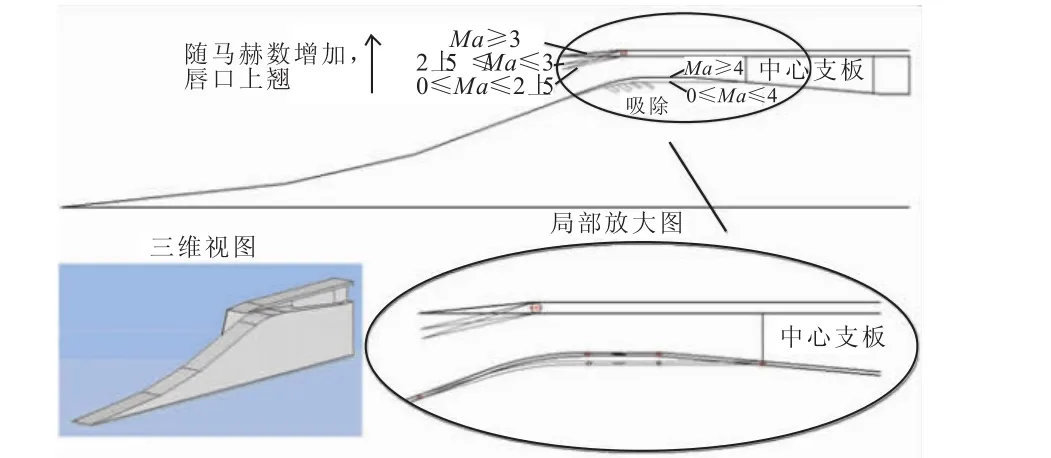
图1 整个工作马赫数范围内的进气道构型示意图形Fig.1 Schematic drawing of the inlet configurations during the whole operating Mach number range

该方案通过调节进气道唇口外罩角度以及喉部高度(调节过程中喉部顶板保持水平)，来改变进气道的几何构型，使不同的工作马赫数区间对应不同的进气道构型。其中，调节唇口外罩角度，可调节进气道的溢流量，从而控制进气道的捕获空气流量;调节进气道喉部高度，可调节进气道能够通过的空气流量。经过上述变几何措施，进气道在不同马赫数区间具有不同的内收缩比和总收缩比。进气道自起动时的内收缩比(Internal Contraction Ratio，后文简写ICR)由Kantrowitz极限确定，起动后的内收缩比介于等熵极限和Kantrowitz极限之间［11］，考虑到吸除槽的存在，可适当放宽内收缩比。本文所有内收缩比的确定，均结合CFD数值模拟得到了验证。

如图1所示，整个工作马赫数范围对应4个进气道构型，构型Ⅰ:Ma=0～2.5，ICR=1.09，喉部高度 69 mm，唇口内表面与水平面夹角 12.5°;构型Ⅱ:Ma=2.5～3(唇口逐步打开的中间状态)，ICR=1.31，喉部高度69 mm，唇口内表面与水平面夹角7.2°;构型Ⅲ:Ma=3～4，ICR=1.63，喉部高度 69 mm，唇口内表面保持水平;构型Ⅳ(设计点构型):Ma=4～7，ICR=1.98，喉部高度56 mm，唇口内表面保持水平。

2 数值模拟方法及校验

本文采用前处理软件Gambit进行进气道建模和网格划分(如图2所示);使用商业计算流体力学软件Fluent求解三维N－S方程，对进气道内外流场进行数值模拟。

在不考虑侧滑角的情况下，进气道的几何形状和流动状态具有对称性。因此，选取进气道的一半作为计算区域。进气道外场两侧均采用对称面边界条件，用来模拟多个并联发动机模块中的单个模块。为了准确模拟湍流，壁面处采取局部加密。在计算区域中，用了压力远场、压力出口和无滑移绝热壁面等边界条件。

数值计算采用基于密度的隐式求解器，应用Roe－FDS矢通量分裂格式。湍流模型采用RNG k-ε模型，近壁区采用标准壁面函数法处理。计算中，用理想气体模型;考虑到变比热和变粘性的影响，采用分段多项式拟合公式计算空气比热，选用Sutherland公式计算空气的粘性。另外，文中若不加说明，则计算云图或等值线图均取自截面Z=48.75 mm(Z为进气道宽度方向，Y为高度方向，X为长度方向)，即支板等宽壁面与隔离段侧壁面的中间面。

图2 进气道计算区域和网格划分Fig.2 Calculation zones and grid generation

Fluent软件在亚音速和超音速流动［12］问题上的计算精度，经在大量工程应用中得到了验证，故文中仅验证其计算高超声速的能力。文献［13］针对某典型二元进气道构型，给出了一系列高超音速风洞实验研究结果。本文以该进气道为例(吸除槽打开且未施加背压)，使用上述数值计算方法进行Ma=7时的CFD计算校验。

图3为实验测量和CFD计算的进气道上、下壁面静压系数对比。可看出，本文的数值模拟方法CFD计算的上、下壁面静压系数变化趋势与实验测量值吻合的很好，两种方法获得的上、下壁面静压系数值许多甚至是相重合的，CFD数值计算的结果很好地反映出了激波后的压升及激波在隔离段内的反射情况。通过该数值校验，可说明本文使用的流体计算软件Fluent以及所采用的计算模型和方法能较准确地模拟高超声速来流条件下的进气道内外流场，计算结果具有较高的可信度。

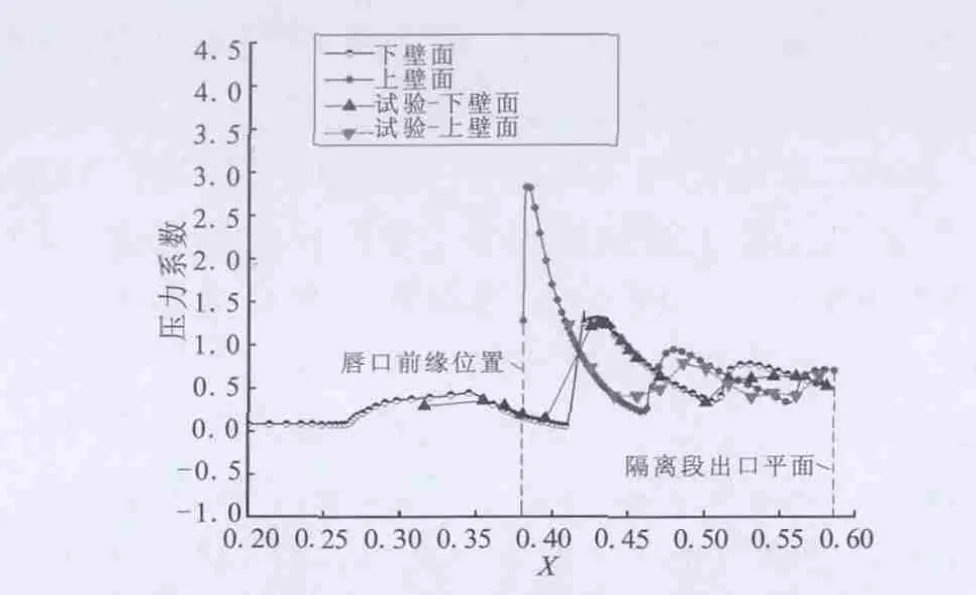
图3 数值模拟和实验结果所得压力系数对比Fig.3 Comparison of the pressure coefficient between numerical and experimental results

3 RBCC变几何进气道性能计算分析

3.1 引射模态性能计算和分析

引射模态是RBCC发动机所特有的一个工作模态，文中引射模态的工作马赫数范围为0～2.5。引射模态下进气道大部分工作时间均处于不起动状态。进气道采用构型Ⅰ时喉道面积最大，可保证有尽量多的空气流量吸入。因引射阶段制约进气量的重要因素之一即为进气道喉道面积的大小［8］，喉道面积越大允许流入的空气流量也越大，在引射模态亚音速阶段，进气道内几乎全部为亚音速流动;此时，进气道与燃烧室部件间存在较强的耦合作用［14］。图4为进气道构型Ⅰ和部分燃烧室在Ma=0.8，飞行高度H=2 km，燃烧室室压 pc=0.092 MPa，主火箭流量 m·R=0.7 kg/s 工况下的CFD计算流场图。可看出，受主火箭喷管扩张比限制，其出口气流处于欠膨胀状态，在室压作用下，主火箭羽流在燃烧室内形成交替的膨胀波和压缩波后，仍保持超音速流动，且该过程中，伴随着羽流范围的不断扩大和对两侧来流空气的挤压。不同进气道构型在引射模态亚音速阶段2个典型马赫数下的性能参数见表1。可看出，设计点构型Ⅳ的喉道高度较低，在同一工况 Ma=0.8，H=2 km，pc=0.092 MPa，m·R=0.7 kg/s下，与构型Ⅰ相比，进气量降低了14.5%。进气道构型Ⅰ在Ma=0.3时，出口静压低于自由来流静压，出口马赫数显著高于来流马赫数，表明来流在进气道内受到抽吸加速。主火箭流量一定时，燃烧室室压波动对RBCC进气道的进气量有显著影响，室压较高时，进气受到抑制，进气量会减少。Ma=0.8主火箭高流量时(主火箭室压也较高)，火箭羽流在燃烧室内膨胀得较厉害，对来流空气的挤压更严重，导致进气量降低。综上所述，采用变几何措施后，可调大进气道的喉道面积，从而增加进气量，但引射模态亚音速阶段制约进气道性能的因素已不局限于进气道本身，主火箭状态及燃烧室室压对进气量等参数有很大影响。

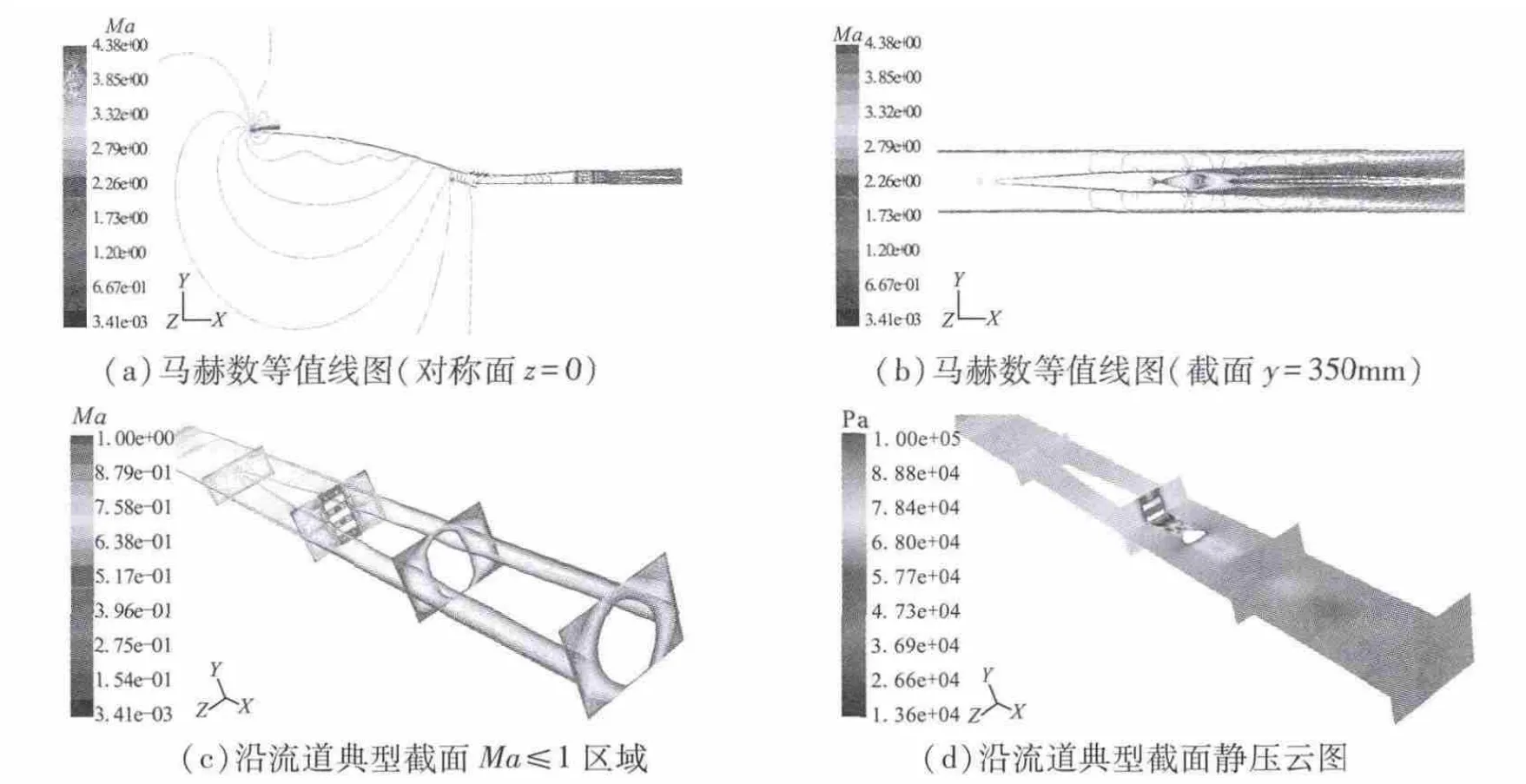
图 4 进气道构型Ⅰ在 Ma=0.8，H=2 km，pc=0.092 MPa，mR=0.7 kg/s工况下 CFD 计算流场图Fig.4 CFD calculation flow field at the condition of Ma=0.8，H=2 km，pc=0.092 MPa，m·R=0.7 kg/s

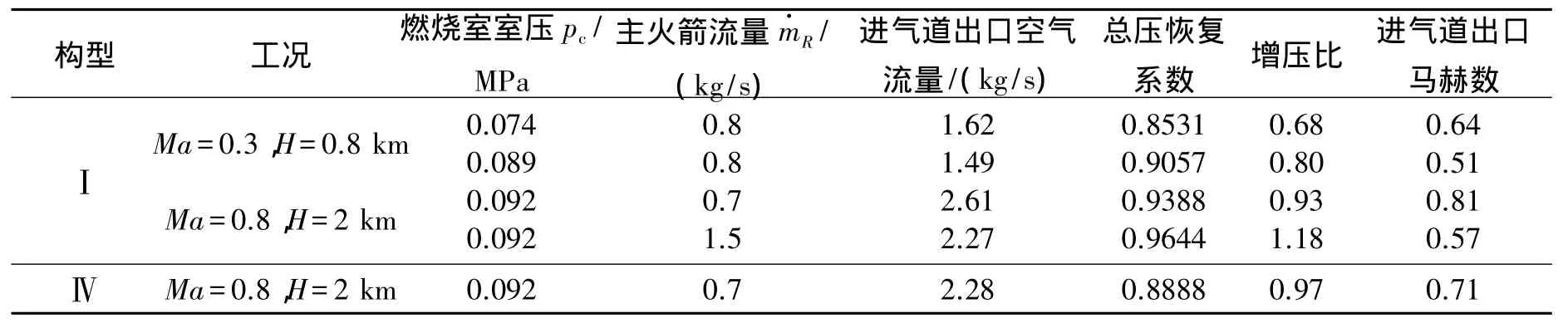
表1 不同进气道构型在引射模态亚音速阶段的性能参数Table 1 Performance parameters of different inlets in the subsonic phase of ejector mode

在引射模态的超音速阶段，主火箭流量逐步减小，来流的冲压作用逐渐占据主导地位。当来流马赫数足够高时，进气道喉部及以后形成超音速流动，燃烧室室压无法直接前传至进气道入口(隔离段内产生激波链起到缓冲作用)，即进气道内通道入口处的流动不受主火箭状态及燃烧室室压的影响;此时，进气道的进气量仅与飞行高度、马赫数及攻角等弹道参数有关。

此外，引射阶段进气道采用构型Ⅰ，其ICR最小，溢流量最大，有利于降低唇口前的弓形激波强度，减小进气道波阻。图5为进气道构型Ⅰ在引射模态超音速阶段若干典型飞行马赫数下(零反压通流状态)计算的内外流场马赫数等值线图。

由图5可见，在低超音速来流Ma=1.5下，进气道存在严重的不起动现象，进气道前部有一道很强的弓形激波;随着马赫数的增加，弓形激波逐渐后移，前体产生的三道斜激波系逐渐清晰，激波角减小，进气道由不起动逐渐向起动状态过渡。Ma=2.3时，进气道处于临界起动状态，唇口前方有一道近似的正激波。表2为进气道在引射模态超音速阶段不同马赫数下的性能参数。可看出，该阶段由于超音速来流马赫数仍较低，进气道的冲压效果相对较差，进气道流量系数、增压比和出口马赫数等参数均较低。随着飞行马赫数增加，进气道流量系数、增压比和出口马赫数逐渐增加;在来流Ma≥1.75以后，进气道出口气流的总压恢复系数先逐渐减小，进气道自起动时(Ma=2.4，见后文)，唇口前方的近似正激波消失，转变为斜激波，激波损失大幅降低，总压恢复系数突增，之后再继续减小。

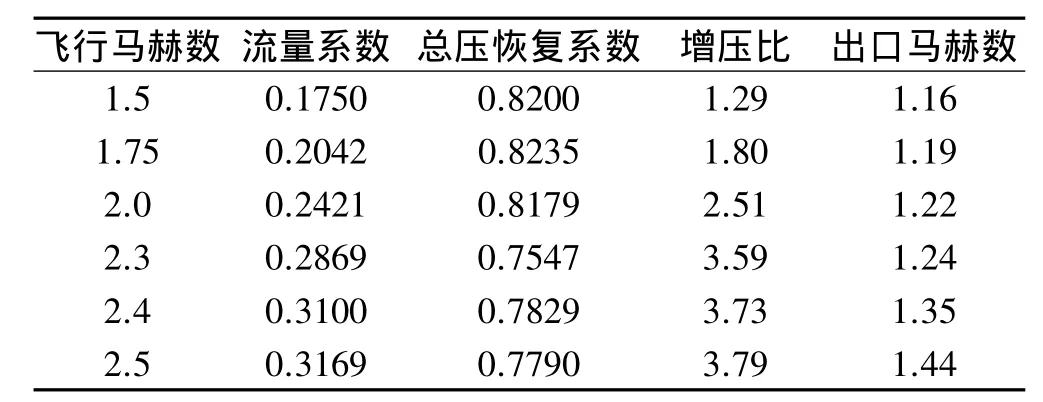
表2 进气道在引射模态超音速阶段性能参数(pb=0)Table 2 Inlet performance parameters in the supersonic phase of ejector mode(pb=0)

3.2 起动性能计算和分析

超音速进气道在低马赫数下都会遇到不起动问题。进气道不起动后其流量系数、总压恢复系数、增压比等参数都有明显下降，性能相对起动时明显恶化。对于RBCC发动机来说，进气道起动马赫数要略低于引射模态向亚燃模态转级的马赫数。文中要求进气道起动马赫数低于2.5。

在RBCC二元进气道的扩张形隔离段内加入中心支板后，受支板前端脱体激波的影响，进气道的起动马赫数略有增加，且幅度很小［12］。随着马赫数增加，进气道构型Ⅰ由不起动到起动的过程(计算中采用上一来流条件下的流场结果作为下一流场的初始条件)如图6所示。由马赫数云图可看出，来流Ma=2时，进气道不起动，进气道唇口前方存在一道弓形激波，该弓形激波与唇口间存在一定间距，且唇口下方的壁面存在流动分离区。Ma=2.3时，进气道处于临界起动状态，唇口附近存在一道“λ”激波。“λ”激波，上半部分为正激波且其后存在滑移线。“λ”激波下半部分存在两个分支，前面分支为一道斜激波(由壁面流动分离区诱导产生)，后面分支为一道正激波。随着飞行马赫数增加，进气道唇口附近的“λ”激波逐渐向进气道内通道方向移动，唇口正激波变为斜激波，附面层分离区减小或消失。Ma=2.4时，进气道完全起动。在Ma=2.5时，进气道唇口楔板顺时针旋转5.3°，由构型Ⅰ转变为构型Ⅱ，可在保证进气道起动的条件下，增大进气道的捕获空气流量和出口静压，减小进气道出口气流马赫数，有利于燃烧室内的燃烧组织。

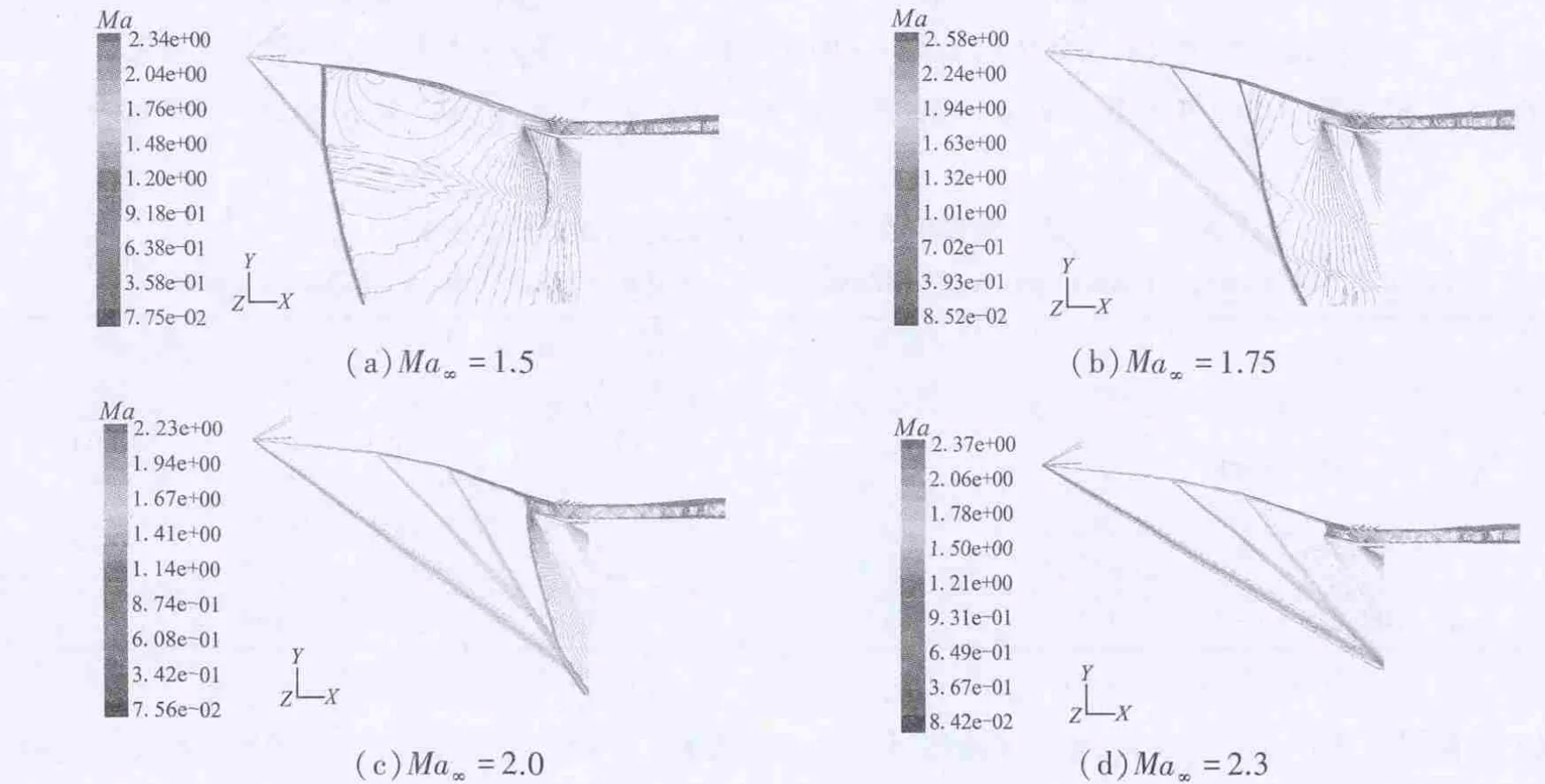
图5 进气道在引射模态超音速阶段不同马赫数下的流场计算马赫数等值线图(pb=0)Fig.5 Inlet Mach contours at different Mach numbers in the supersonic phase of ejector mode(pb=0)

3.3 亚燃和超燃模态性能计算

文中RBCC发动机亚燃、超燃模态工作马赫数区间为2.5～7，这两个模态是RBCC发动机工作马赫数区间跨度最大的模态，其性能高低直接影响发动机的整体性能指标，而进气道则为发动机燃烧室的稳定燃烧提供必要的条件。图7为零反压时，RBCC变几何进气道在亚燃和超燃模态若干典型马赫数下的CFD计算流场图。

表3为进气道不同构型在不同马赫数下的出口性能参数。可看出，在Ma=2.5时，进气道构型由Ⅰ转变为Ⅱ后，进气道性能有显著提升。其中，流量系数提高了11.4%，出口总压恢复系数提高了4.5%，出口增压比提高了29.8%。然而，构型Ⅱ若在Ma≥3的来流条件下继续工作，其对捕获空气的压缩程度会越来越不足，表现为进气道出口马赫数偏高，且增压比偏低。例如，Ma=3.6时，进气道构型Ⅱ出口马赫数接近2，当存在反压时，在结尾正激波作用下，进气道总压恢复系数很低，难以正常使用。事实上，在Ma=3.0时，构型Ⅱ转变为构型Ⅲ，不仅流量系数可增加13.1%，还可显著降低进气道出口气流马赫数，并显著提高进气道增压比。Ma=4时，构型Ⅲ转变为Ⅳ，进气道流量系数、增压比略有下降，但可显著提高进气道抗反压能力(见后文)。综上所述，采用变几何措施后，RBCC进气道的整体性能有了明显提升，可保证亚、超燃模态不同马赫数下进气道均具有适中的总压恢复系数、出口气流马赫数、增压比等性能参数(对比文献［8］中RBCC进气道)，能满足RBCC发动机燃烧室对进口空气参数的要求。

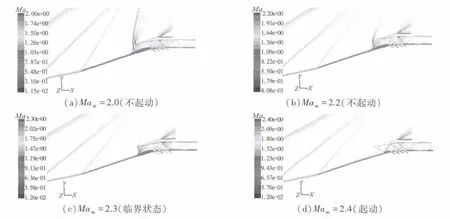
图6 随马赫数增加进气道(构型Ⅰ)自起动过程示意图Fig.6 Inlet(configurationⅠ)starting process as flight Mach number increasing

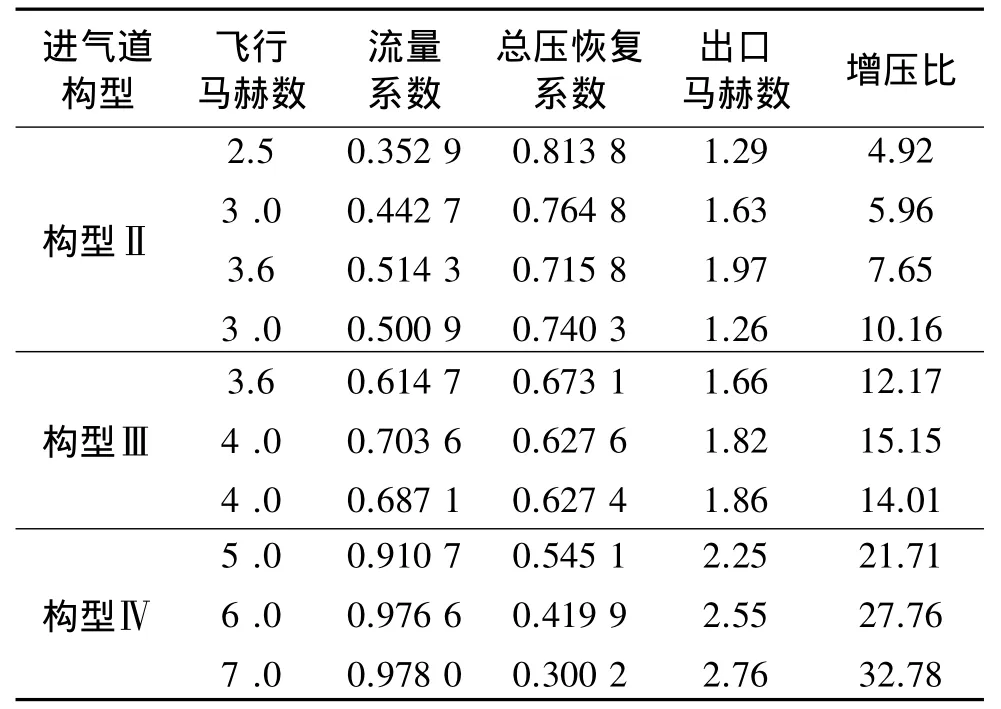
表3 进气道在亚燃和超燃模态下的性能参数(pb=0)Table 3 Inlet performance parameters in ramjet and scramjet mode(pb=0)

3.4 抗反压性能计算和分析

进气道的抗反压能力越高，允许的燃烧室室压越高，发动机稳定工作的裕度越高。发动机尺寸一定时，室压越高，则推力越大。因此，进气道较强的抗反压能力对提升发动机的推力具有重要意义。通常进气道所能承受最大反压的绝对数值取决于进气道结构参数设计(RBCC二元进气道加入中心支板后，对其抗反压性能的影响可参考文献［12］)以及飞行弹道。当飞行马赫数一定时，飞行高度越低，自由来流静压越高，进气道抗反压的绝对数值越高，但进气道所能承受的最大反压与自由来流静压之比(pmax/p∞，称为极限反压比)仅与飞行马赫数相关，与飞行高度基本无关。

随着进气道出口反压增加，隔离段激波串位置不断前移，进气道出口气流马赫数逐渐降低，气流减速效果越来越明显。本文将使隔离段激波串前端抵达进气道喉部吸除槽附时的反压视为进气道所能承受的最大反压值pmax。图8为进气道在Ma=3、H=10 km工况下不同出口反压时的静压分布云图。表4为该变几何进气道在几个典型来流马赫数下的抗反压性能参数。本文进气道Ma=5时，能够承受的极限反压比比文献［15］中的RBCC进气道提高了54.5%;Ma=6时，提高了14.0%。需特别说明的是采用变几何措施后，进气道的抗反压能力有明显提升。以Ma=4、H=18 km工况为例(对比结果见图9和表5)，构型Ⅲ所能够承受的最大背压为0.38 MPa，降低喉道高度变成构型Ⅳ，则可承受的最大背压为0.45 MPa，抗反压能力提升了18.4%。构型Ⅳ在较高反压作用下，其出口气流马赫数更低，且由于激波串前端所在位置处气流马赫数较低，激波强度较低，构型Ⅳ出口气流的总压恢复系数反而高于构型Ⅲ。

表4 不同马赫数下进气道的抗反压能力Table 4 Inlet＇s resistance to back pressure at different Mach numbers

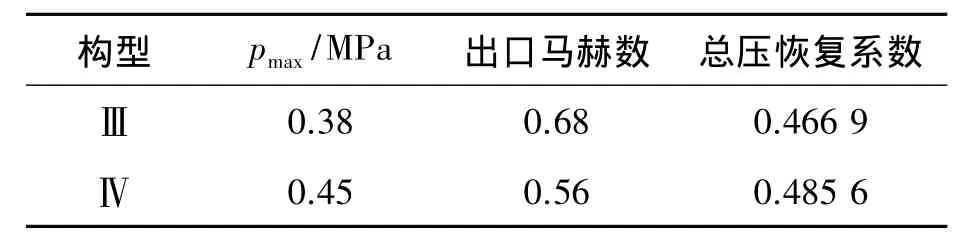
表5 Ma=4，H=18 km工况下两种构型抗反压性能对比Table 5 Comparison of resistance to back pressure at Ma=4，H=18 m between two configurations

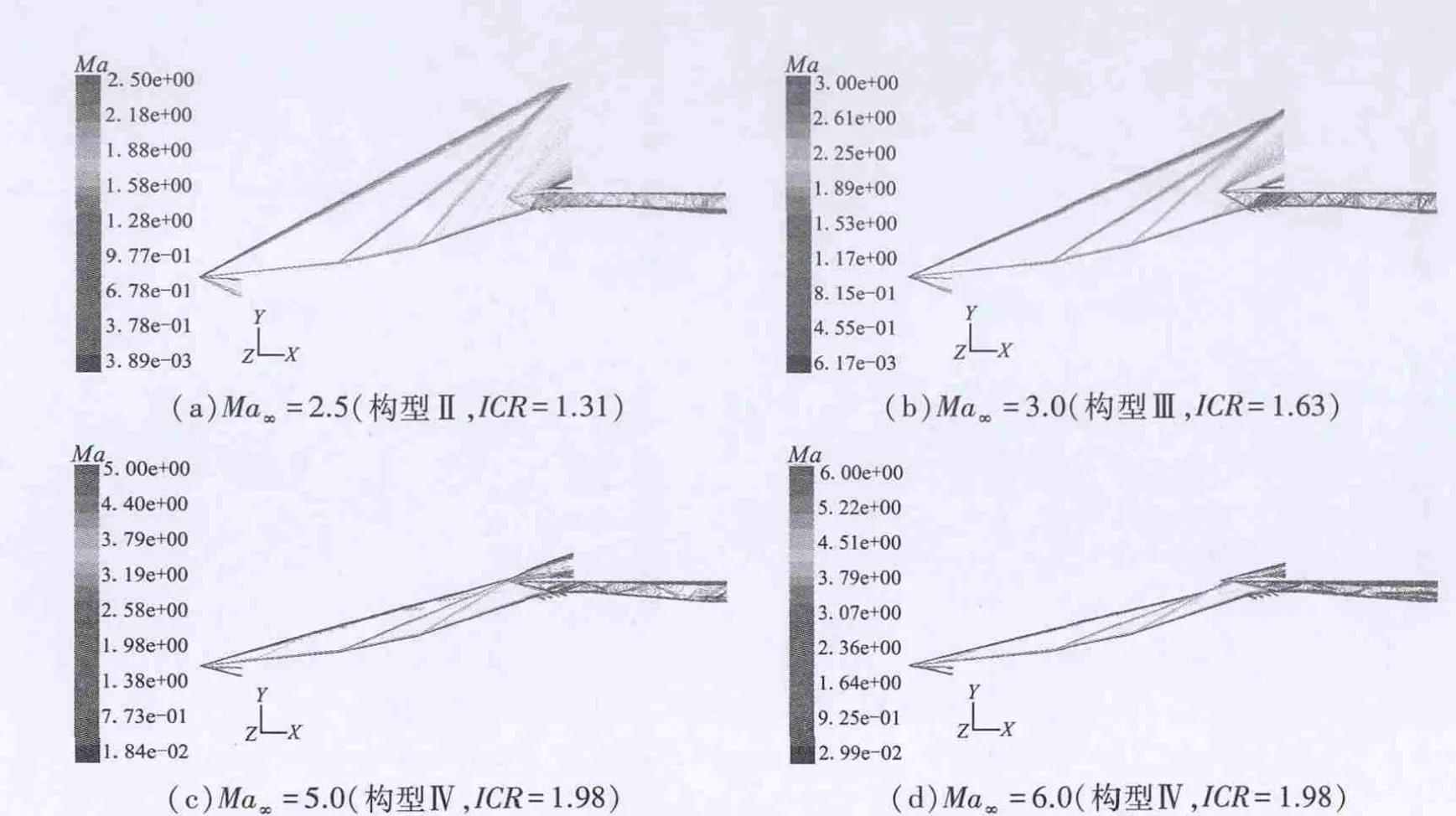
图7 进气道零反压下的流场计算马赫数等值线图Fig.7 Mach number contours of the inlet at the condition of pb=0

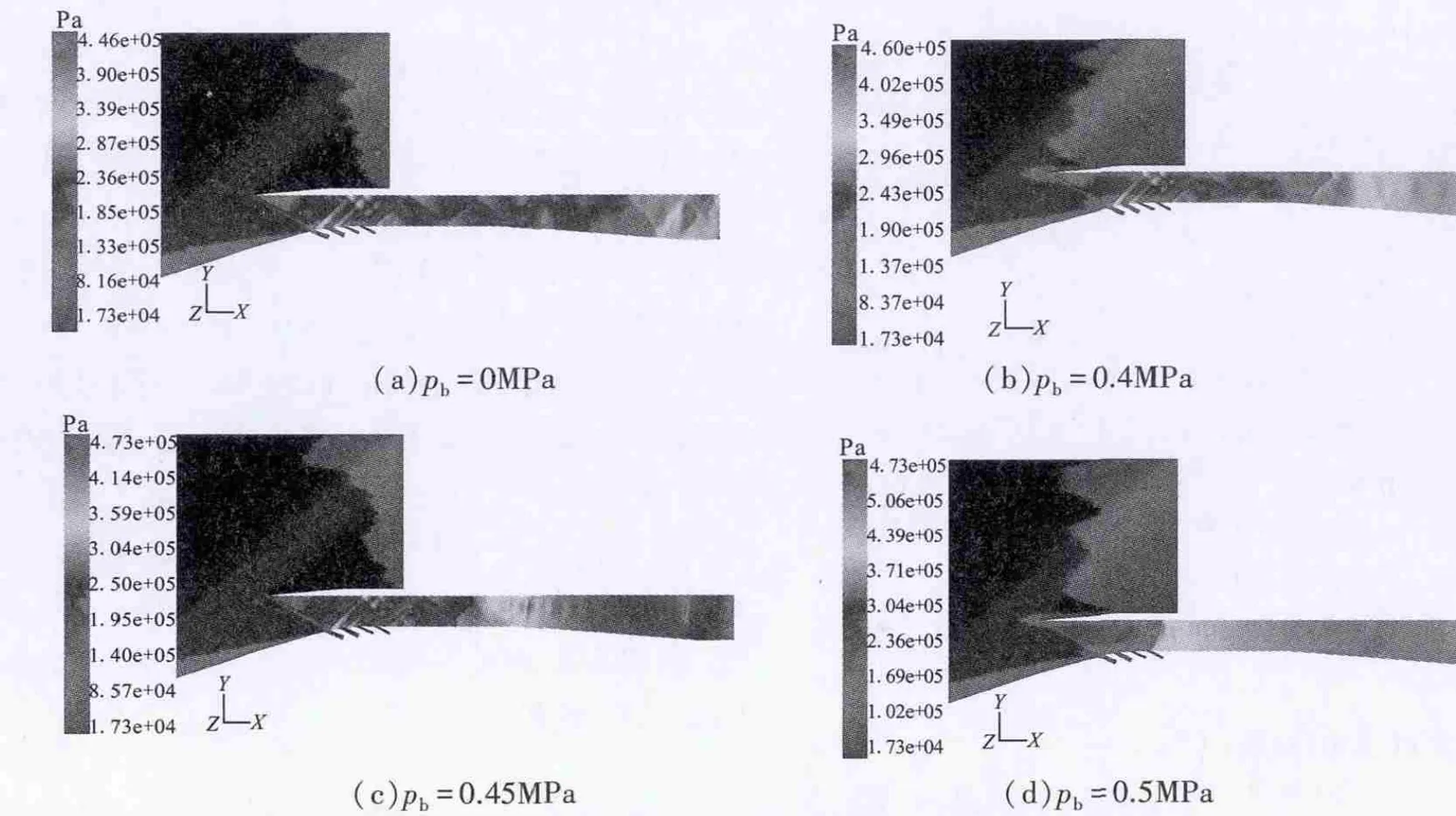
图8 进气道在不同反压下的静压分布Fig.8 Static pressure distribution of the inlet at different back pressure

4 结论

(1)在引射模态亚音速阶段，采用变几何措施增大进气道喉道面积，可增加进气量，而制约进气道性能的因素已不局限于进气道本身，主火箭状态及燃烧室室压对进气量也有很大的影响;

(2)通过采取变几何和吸除措施，进气道能在Ma=2.4时，实现自起动，为引射模态向亚燃模态顺利转级提供了必要条件;

(3)RBCC变几何进气道通过主动调节溢流量，降低了起动马赫数，初步解决了高低马赫数下进气道对来流压缩量要求不同的矛盾，显著拓宽了进气道在起动状态下正常工作的马赫数范围(文中为2.4～7);

(4)在亚燃和超燃模态的不同马赫数范围内，通过采取变几何调节措施，进气道出口各项主要性能指标适中，可满足RBCC燃烧室入口对来流空气参数的要求;

(5)采用变几何措施，还可提高进气道的抗反压能力，从而允许存在较高的燃烧室压力，有利于提升发动机推力。

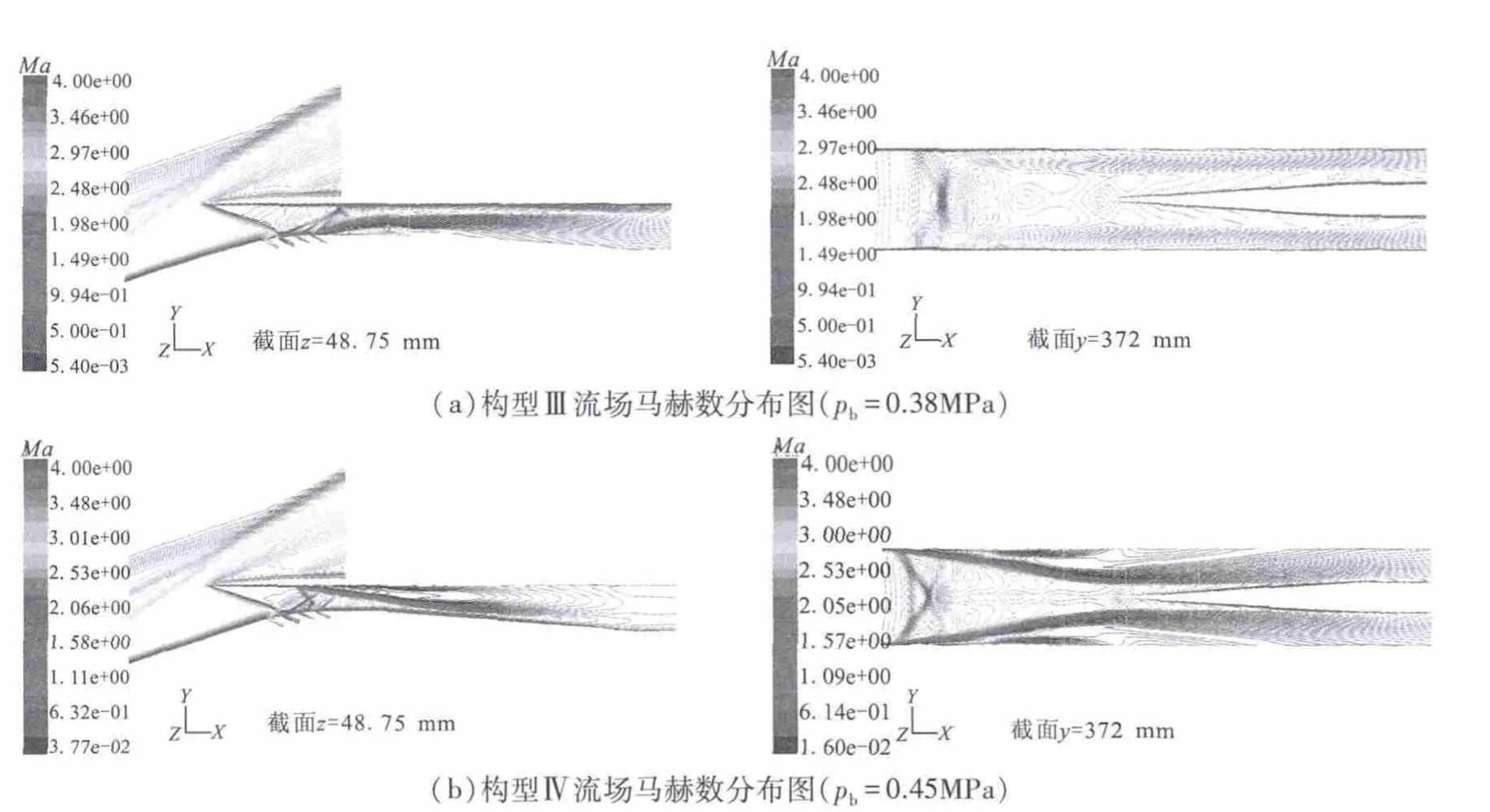
图9 Ma=4、H=18 km工况下两种不同进气道构型抗反压性能对比Fig.9 Comparison of resistance to back pressure at Ma=4，H=18 km between different configurations

［1］Mel Bulman，Adam Siebenhaar.The strutjet engine:Exploding the myths surrounding high speed airbreathing propulsion［R］.AIAA 95－2475.

［2］黄生洪，何洪庆，何国强，等.火箭基组合循环(RBCC)推进系统概念设计模型［J］.推进技术，2003，21(1):1－5.

［3］蔡飞超，陈凤明，徐东来，等.宽Ma数范围固定几何进气道设计问题研究［J］.固体火箭技术，2010，33(2):163－166.

［4］DeBonis J R，Trefny C J，Steffen C J.Inlet development for a rocket based combined cycle，single stage to orbit vehicle using computational fluid dynamics［R］.AIAA 99－2239.

［5］Scott R Thomas，H Douglas Perkins and Charles J Trefny.E－valuation of an ejector ramjet based propulsion system for airbreathing hypersonic flight［R］.NASA TM－107422.

［6］张晓嘉，梁德旺，李博，等.典型二元高超声速进气道设计方法研究［J］.航空动力学报，2007，22(8):1291－1296.

［7］黎明，宋文艳，贺伟.高超声速二维混压式前体/进气道设计方法研究［J］.航空动力学报，2004，19(4):459－465.

［8］刘晓伟.火箭基组合循环(RBCC)动力宽适用性进气道研究［D］.西安:西北工业大学，2010.

［9］丁海河，王发民.高超声速进气道起动特性数值研究［J］.宇航学报，2007，28(6):1482－1487.

［10］袁化成，梁德旺.抽吸对高超声速进气道起动能力的影响［J］.推进技术.2006，27(6):525－528.

［11］范晓樯.高超声速进气道的设计、计算与实验研究［D］.长沙:国防科技大学，2006.

［12］石磊，何国强，秦飞，等.某RBCC样机进气道的设计与数值模拟［J］.航空动力学报，2011，26(8):1801－1807.

［13］Häberle J and Gülhan A.Investigation of two－dimensional scramjet inlet flow field at Mach 7［J］.Journal of Propulsion and Power，2008，24(3):446－459.

［14］李宇飞.RBCC引射火箭模态性能研究［D］.西安:西北工业大学，2004.

［15］Yungster S，DeBonis J R.Computational analysis of hypersonic inlet flow in a rocket－based combined－cycle engine［J］.AIAA 97－0028.