汽化效应对燃气蒸汽式弹射气液两相流场的影响①

刘伯伟，姜 毅

(北京理工大学 宇航学院，北京 100081)

0 引言

燃气蒸汽式弹射被广泛用于陆基及潜射战略导弹的发射系统中，与其他弹射形式相比，具有结构简单、温度适中、压力输出平稳、输出能量可调等优点［1］。该方式通常使用液态水作为冷却介质，通过液态水的热传导和汽化吸热两种方式对燃气进行降温，其发射过程非常复杂，涉及燃气射流、气液两相流、传热、汽化传质等多方面内容。传统的零维内弹道算法不考虑流体参数沿管路轴线的变化，且无法给出流场中液相的流型，也就无法具体研究冷却水的汽化过程及流场中各处的流动状态，而应用计算流体力学技术(CFD)求解气液两相流场，可较好地解决这一问题。

某型集中注水式燃气蒸汽弹射装置采用高能双基药作为能量源，并使用液态水作为冷却介质，本文对其建立了二维轴对称两相冻结流场计算模型，使用Mixture多相流模型求解气液两相冻结流场，使用组分输运模型将流场中的气相工质简化为包含燃气、水蒸汽和空气3种组分的混合气体，利用水的汽化模型模拟了水的汽化过程，利用动网格技术模拟了发射过程中的流场变化，研究了汽化效应对流场产生的影响。

1 物理模型

1.1 多相流模型中的组分输运方程

不考虑流场中的化学反应［2］，组分输运模型中第i组分守恒方程统一形式为

与单一组分的流场守恒方程相比，式(1)中增加了组分i的质量分数项Yi。如果总的组分数为N，则有

计算时，需要求解前N－1种组分的守恒方程，而第N种组分的质量分数可由式(2)求得。

当把式(1)应用于多相流模型中，对q相的第i种组分，式(1)变为

式中 αq为q相的体积分数qjpi为由q相第j组分到p相第i组分的质量转移源项piqj依此类推。

1.2 真实气体模型

在导弹发射过程中，流场中除燃气外，还存在液态水汽化而来的水蒸汽，以及初始时刻的少量空气。当压力小于20 MPa、温度大于1 400 K时，可将燃气和空气作理想气体处理，但由于水蒸汽离液态不远，将其简化为理想气体具有一定偏差。因此，有必要将水蒸汽作真实气体考虑［3］。

对水蒸汽应用Soave-Redlich-Kwong真实气体模型［4－6］:

其中

该模型需要提供3个参数，即临界温度Tc、临界压力pc、偏心因子ω。

1.3 水的汽化方程

根据水的饱和温度计算水的汽化率，对计算域中各个网格内的气相和液相流体分别求解。当混合相温度大于水的饱和温度，水吸收能量汽化为水蒸汽;当混合相温度小于水的饱和温度时，水蒸汽释放能量凝结为液态水［7］。

液态水汽化公式

水蒸汽凝结公式

某一单元格内液态水的净汽化率为

水汽化造成的能量变化为

式中 Sh为水汽化吸收的能量或水蒸汽凝结释放的能量，当m·为正，表示当前单元格内总体表现为液态水汽化吸热，流场能量降低，Sh为负，反之亦同;Qlat为水的汽化潜热，根据当地压力查饱和水与和饱和蒸汽表得到。

2 计算模型

2.1 计算域

计算域采用二维轴对称模型，由喷管、水室、雾化器、低压室、弹托等部分组成，如图1所示。其中，水室中存放着冷却水。整个流场均采用四边形网格划分，因雾化器开孔较细小，故对雾化器开孔附近的网格进行了加密，如图2所示。

图1 计算域示意图Fig.1 Diagram of computational domain

图2 雾化器附近网格示意图Fig.2 Diagram of mesh nearing atomizer

2.2 边界条件

图3为边界条件示意图。喷管入口处为压力入口边界，需要给定入口的总温、总压，其中总温为3 000 K，总压由发动机空放试验得到，如图3(b)所示;计算域下边界为轴对称边界;其余外边界为壁面边界，物面边界采用无滑移绝热壁面边界条件，近壁面湍流计算采用标准壁面函数模型;其中，弹托壁面为运动边界，计算时需要积分此面上的混合相工质静压，从而得到导弹某一时刻的运动加速度，并结合动网格技术实现计算域的变形。由于弹托壁面附近的网格非常规整，故使用动态分层法生成新网格。

图3 边界条件示意图Fig.3 Diagram of boundary conditions

2.3 初始条件

计算初始时刻由高压室破膜时刻开始，破膜压力为 2 MPa，预加冷却水量为 2.20 kg。

2.4 工况介绍

计算分为2种工况。其中，工况1未考虑汽化效应，液态水仅以热传导的形式为燃气降温，并没有水蒸汽生成，故将气相工质简化为单一组分的理想燃气，液相为不可压缩的液态水;工况2引入汽化模型和组分输运模型，液态水汽化为水蒸汽，将气相工质看作燃气、水蒸汽和少量空气3种组分的混合气体，通过引入Soave-Redlich-Kwong模型，将水蒸汽看作真实气体。

3 结果与分析

3.1 气液两相流场分布

以工况2为例，图4为工况2初始时刻和离筒时刻的流场示意图，对称轴上方为初始时刻流场示意图，预加冷却水加于水室中，如图4所示;对称轴下方为离筒时刻流场，此时流场轴向长度约为初始时刻的6.6倍。

图4 发射前后流场对比示意图Fig.4 Diagram of computational domain after and before launching

图5为破膜后0～10 ms流场中的液态水和水蒸汽分布图。图5(a)中，燃气将液态水冲向低压室，经过雾化器后，一方面液态水可较均匀地分布于整个低压室，从而减少燃气对弹托底部的直接冲击;另一方面，可增大燃气和液态水的交界面，有利于液态水的汽化。

图5(b)中，初始时刻流场中并没有水蒸汽，随着与燃气交界处的液态水被加热，其温度超过了饱和温度，从而在交界面处被汽化为水蒸汽。由于生成的水蒸汽主要分布于燃气与液态水的交界面处，故水蒸汽充当了燃气与液态水的能量传递中介。

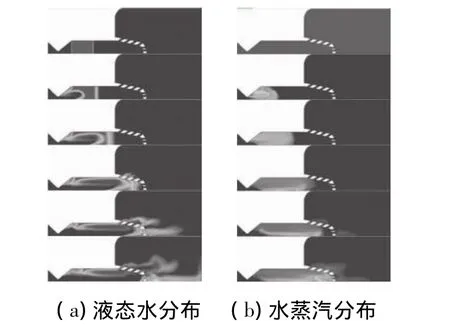
图5 前10 ms液态水和水蒸汽分布Fig.5 Distribution of water and vapor in 0～ 10 ms

空放试验中，利用高速摄影仪拍摄了雾化器后方流场。点火后，首先冲过雾化器的是水室中预加的液态水，随后燃气进入流场，图6为从中截取的液态水分布图。由图6可知，穿过雾化器后，原先集中于水室中的液态水变为散布于后方流场，大部分液态水分布于流场的轴线附近，只有少部分液态水由雾化器侧面的开孔排出。图5(a)的仿真结果与高速摄影中的液态水分布非常一致，证明Mixture模型能较好地模拟流场中液相的分布，验证了仿真结果的可靠性。

图7为工况1和工况2中液态水的质量变化曲线，为加以区分，工况1加实心方块，工况2加空心方块，下文类同。工况1因为未加汽化模型，水的质量不变。工况2初始时刻水的汽化较慢，这是因为初始时刻燃气与液态水的交界面较小;0.2 s后，随着燃气与液态水的混合越来越充分，液态水的汽化速度逐渐加快;0.48 s后，由于大部分液态水已经汽化，燃气与液态水的交界面开始减小，水的汽化速度也开始减慢;最终液态水剩余 0.208 kg，与预加的 2.20 kg相比，汽化率达到94.5%，汽化效果较好。

图6 液态水分布的高速摄影图片Fig.6 High speed photograph of water distribution

图7 液态水的质量Fig.7 Mass of water

3.2 汽化效应对内弹道性能的影响

图8为低压室中以质量平均的混合工质平均静温曲线。2种工况的温度均在离筒时刻达到最大值，但工况1的温度曲线在离筒前单调上升，且在离筒时刻达到最大值1 113 K;工况2的温度曲线先上升，并在0.23 s达到极大值546 K，随着汽化速度的加快，温度转而降低，0.45 s后剩余液态水较少，汽化速度减慢，温度再次上升，并在离筒前达到最大值589 K。可预见，适当增加预加水量，可使工况2的温度进一步降低。美国MX导弹采用燃气蒸汽式弹射后，使工质温度降低到477～533 K［8］，工况2与此温度范围吻合，而工况1则偏差过大。由此可见，与只考虑热传导降温相比，考虑汽化效应能大幅降低流场的温度。

图9为弹托底部平均静压曲线，2种工况的压力曲线变化趋势基本相同，且均在0.21 s达到最大值，但工况2的压力变化比工况1更加剧烈，上升与下降速度均快于工况1。0.48 s后，由于液态水的汽化减慢，流场温度上升，工况2的压力转为上升，并使其离筒压力高于工况1。与图8的低压室平均静温相比，汽化效应对压力的影响较小。这是因为不考虑汽化效应时，虽然流场中的气相工质没有增加液态水汽化而来的水蒸汽，但同时也未考虑汽化所吸收的能量损失，造成仿真流场中的温度升高，根据理想气体状态方程，温度升高造成压力相应升高，故而压力损失并不明显。

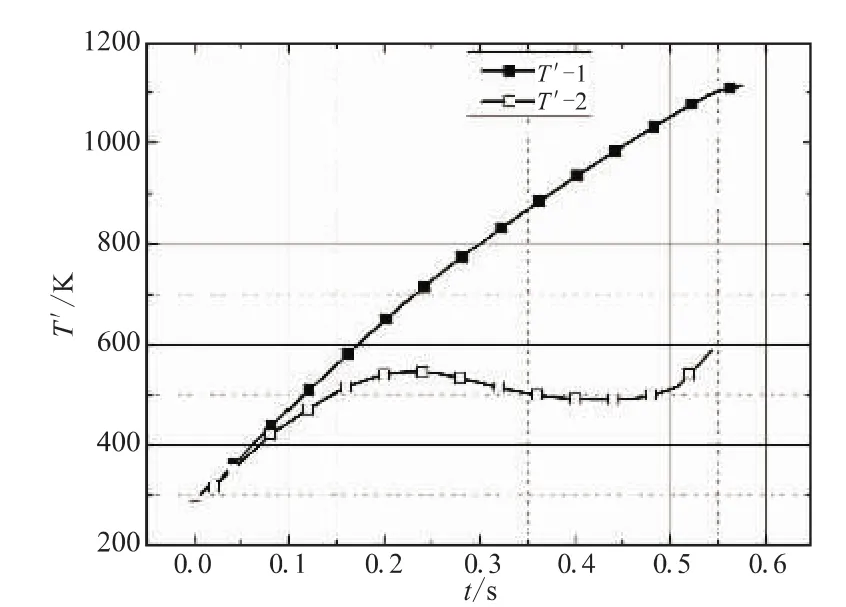
图8 低压室平均静温Fig.8 Average static temperature of low-pressure chamber

图9 弹托底部平均静压Fig.9 Average static pressure nearing sabot

图10为弹托底部平均静温曲线，图11为0.12 s两工况的流场温度云图，对称轴之上为工况1，对称轴之下为工况2。0.12 s后，2种工况的高温燃气都将低压室中的液态水排向两侧，对弹托产生了一定的直接冲击，但工况1的冲击作用更加明显，最高温度达到了987 K;而工况2由于考虑了汽化效应，在燃气和液态水的交界面处，由于汽化吸热对燃气的降温作用较明显，同时汽化生成的水蒸汽比热容要高于燃气，对降温也有一定效果，工况2的最高温度仅为764 K。

图12与图13分别为导弹加速度和速度曲线，结合图9，由于弹托底部压力的变化趋势基本一致，故2种工况的加速度与速度曲线趋势也相近，但由于工况2弹托底部压力略高于工况1，故工况2的最大加速度与离筒速度均高于工况1。

图10 弹托底部平均静温Fig.10 Average static temperature nearing sabot

图11 0.12 s流场温度云图Fig.11 Temperature contours at 0.12 s

图12 导弹加速度Fig.12 Acceleration of missile

图13 导弹速度Fig.13 Velocity of missile

表1列出了两种工况下部分内弹道参数与对应的试验值，考虑汽化效应的工况2与试验值更加一致，误差均在6%以内，而没有考虑汽化效应的工况1，则误差较大。

表1 内弹道参数的对比Table 1 Comparison of interior ballistic parameters

4 结论

(1)与不考虑汽化效应相比，考虑汽化效应使仿真流场的最大平均温度降低了524 K，弹托底部的最大平均温度降低了223 K，二者降低的幅度分别达到47.1%和22.6%。虽然不考虑汽化效应也能得到接近试验结果的压力与速度曲线，但误差相对较大，尤其温度误差过大，难以反映流场中的真实情况，从而无法对弹射装置的设计与改进提供可靠性指导。所以，在该类问题的仿真中必须考虑汽化效应。

(2)结合Mixture模型与液态水汽化模型能较好地模拟发射过程中液态水的流型与汽化过程。

(3)Soave-Redlich-Kwong真实气体模型能准确地反映发射过程中水蒸汽的状态变化，从而给出准确的内弹道结果。

［1］芮守祯，邢玉明.几种导弹弹射动力系统内弹道性能比较［J］.北京航空航天大学学报，2009，35(6):766-770.

［2］袁曾凤.火箭导弹弹射内弹道学［M］.北京:北京工业学院出版社，1987.

［3］赵险峰，王俊杰.潜地弹道导弹发射系统内弹道学［M］.哈尔滨:哈尔滨工程大学出版社，2001.

［4］康玉东，孙冰.燃气非平衡流再生冷却流动传热数值模拟［J］.推进技术，2011，32(1):119-124.

［5］佘守贤.真实气体与气液相变［M］.北京:人民教育出版社，1963.

［6］Soave G.Equilibrium constants from a modified redlich-kwong equation of state［J］.Chemical Engineering Science，1972，27(6).

［7］LEE W H.Pressure iteration scheme for two-phase flow modeling［J］.Ieee/engineering in Medicine and Biology Society Annual Conference，1980(1).

［8］李广裕.战略导弹弹射技术的发展［J］.国外导弹与航天运载器，1990(7):38-49.