基于遗传算法的无刷直流电动机自适应模糊控制
2014-03-12侯春杰孟令瑞
侯春杰,张 雷,孟令瑞
(河南科技大学,洛阳471023)
0 引 言
由于无刷直流电动机(以下简称BLDCM)具有功率密度高、体积小、调速性能好且结构简单的特点,它在汽车、工具、工业工控、航天等领域应用广泛[1-3]。
目前采用遗传算法(以下简称GA)优化模糊控制器的研究有很多[4-9]。文献[7]采用了十进制的遗传算法编码方式,可以得到全局最佳规则库,仿真结果较好。文献[8]通过实数编码的GA 对隶属度函数的位置及宽度进行共同编码,引入适当的隶属度函数评判机制来生成最优的隶属度函数,仿真结果表明优化后的模糊控制器控制品质有较大的改善和提高。文献[9]提出了二维调整因子的概念,利用GA 优化选取二维调整因子、量化因子以及比例因子,减小了搜索空间。
本文利用GA 同时优化控制规则和隶属度函数,并在MATLAB/Simulink 中搭建仿真模型,将遗传算法与自适应模糊控制相结合[10-11]。仿真表明,基于该方法的BLDCM 自适应模糊控制系统,响应快、无超调、稳态误差小,并且具有较强的自适应性和鲁棒性。
1 无刷直流电动机双闭环控制系统
1.1 BLDCM 的数学模型
本文数学模型采用两相导通星形三相六状态,并满足以下假定:
1)转子磁阻不随位置变化而变化,三相绕组完全对称;
2)不计电枢反应、换相过程和齿槽的影响;
3)在定子内表面,电枢导体呈均匀连续分布;
4)磁路不饱和,忽略磁滞损耗以及涡流损耗。
基于以上假设,三相对称BLDCM 的相电压方程:
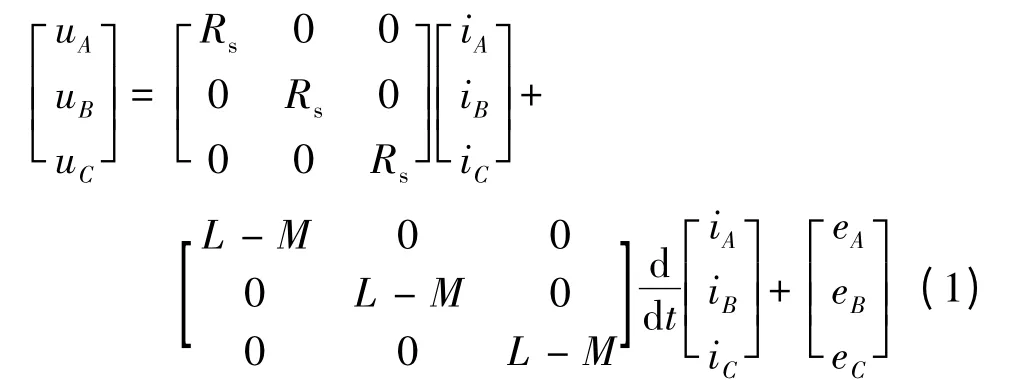
式中:eA,eB,eC为反电动势;iA,iB,iC为三相定子绕组的相电流;uA,uB,uC为三相定子绕组的相电压;Rs为绕组电阻;L 为自感;M 为互感。
电磁转矩的方程:
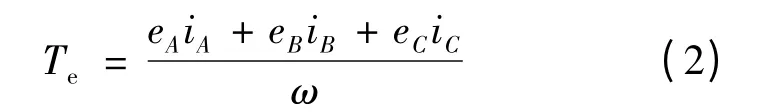
转子运动方程:
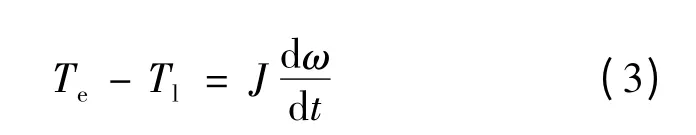
式中:Te为电磁转矩;ω 为转子机械角加速度;Tl为负载转矩;J 为转子的转动惯量。
1.2 双闭环控制系统
速度环采用Fuzzy 控制器为外环,并使用GA 对其进行优化,优化后的Fuzzy 控制器输入为给定转速n*与实际速度回馈值n 的差值,输出为内环的给定值。内环为PI 调节器组成的电流环,外环输出的给定电流值i*减去采样值i 作为PI 调节器的输入,输出为BLDCM 的给定电压。采用这种双闭环控制策略,能恰当地发挥速度负反馈和电流负反馈的作用,使控制系统具有良好的动、静态特性。图1 为BLDCM 双闭环控制系统的结构图。
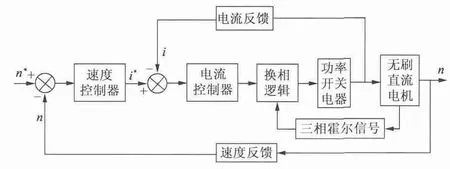
图1 BLDCM 双闭环控制系统的结构图
2 GA 优化自适应模糊控制
2.1 个体编码
对于隶属度函数的形状,本文选择三角形隶属度函数,采用十进制编码方式。其可由3 个变量确定:左右端点的横坐标以及顶点横坐标。如图2 所示,选取三点横坐标作为优化参数,即对{x1,x2,x3,x4,x5}进行编码。对于两输入三输出的系统而言,其隶属度函数的编码为5 ×5 =25 的编码串。
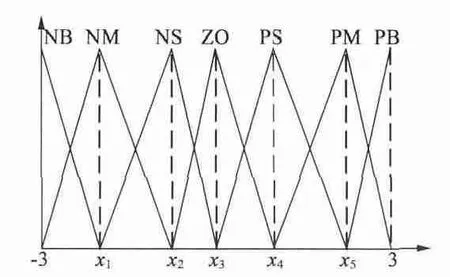
图2 模糊变量的隶属度函数图形
对于控制规则的编码,约定1 代表NB,2 代表NM,3 代表NS,4 代表ZO,5 代表PS,6 代表PM,7代表PB,模糊规则可拉伸成147 位的数字编码串。
将隶属度函数和控制规则的编码联合起来,就得到长度为25 +147 =172 位的染色体编码串。
2.2 适应度函数
本文目标函数采用误差绝对值时间积分性能指标,加上系统输出的二次方项以免控制量太大,加入惩罚函数防止超调,如果超调,就将超调量加入最佳指标式子中。
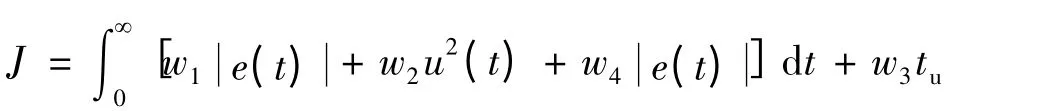
式中:u(t)为控制器输出;e(t)为系统误差;w1,w2,w3,w4为权值,且w4≫w1,tu为上升时间。
因种群收敛可能出现除零,所以将适应度函数设为fit=1/(1 +J)。
2.3 选择操作
2.4 交叉算子
编码串的前25 位是隶属度函数的编码,后147位为规则编码。假若按照一般的交叉方法,容易产生一些病态或者不合理的后代。因此本文采用分步一致交叉方法。对于前25 位隶属度函数的编码,因有5 个变量,所以分成5 组,每组5 位编码,组与组之间进行交叉互换。对于后147 位规则的编码,首先将等位基因比较,若其差值绝对值小于或者等于1,则等位基因可以互换,因此可防止控制作用发生突变及其引起的控制系统的剧烈震荡。
2.5 变异算子
分步进行隶属度函数和规则的变异操作。对于前25 位编码,若变异的概率小于0.01,并且变异位加上1 仍小于后面的的数时,实施变异。针对后147 位编码,如果变异概率小于给定变值,则变异位基因值+1 或-1。变异后的数字小于1 时令该基因值等于1,大于7 时令该基因值等于7。为防止产生不合理规则,变异量只能是+1 或者-1。
表1 至表3 为GA 优化后的控制规则。
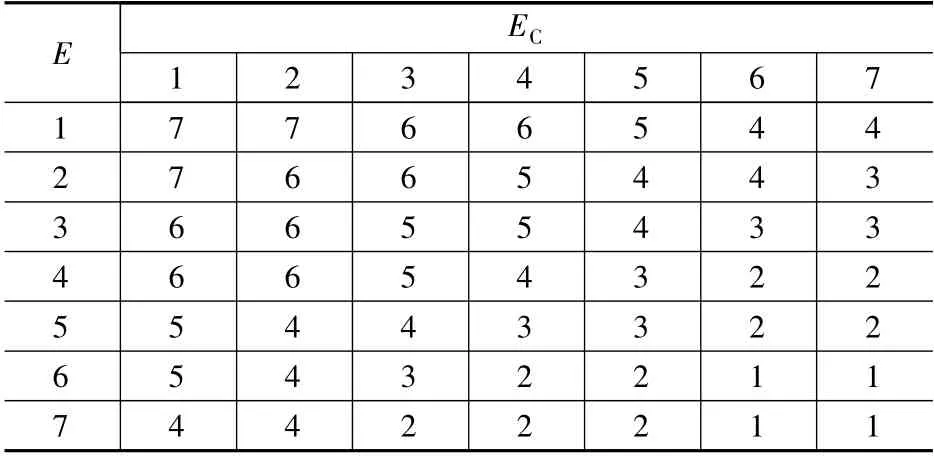
表1 Δkp 优化规则表
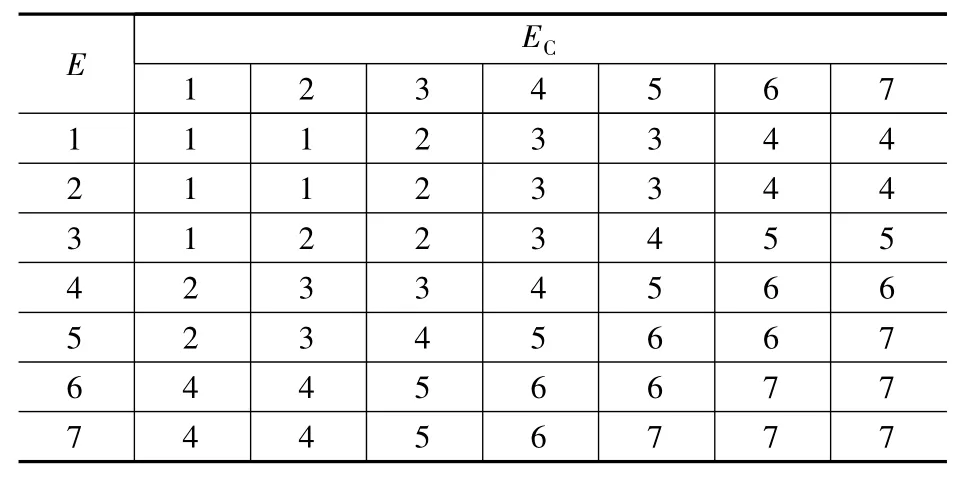
表2 Δki 优化规则表
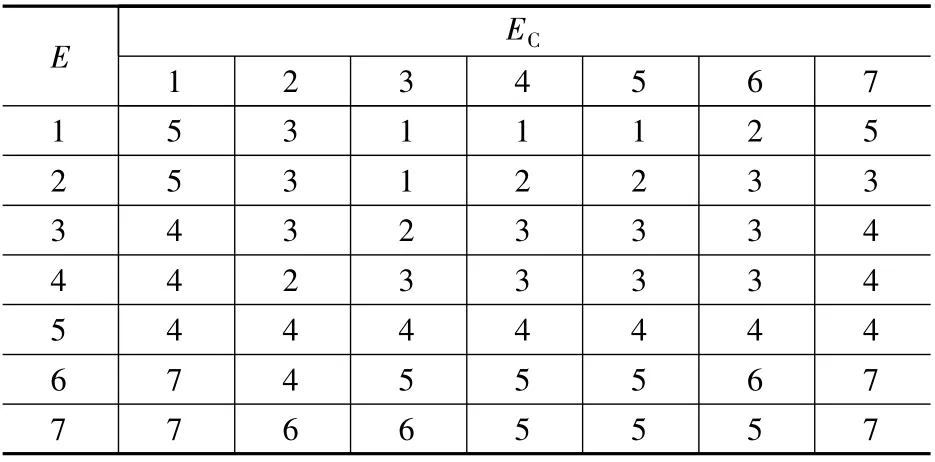
表3 Δkd 优化规则表
2.6 基于GA 优化的自适应模糊控制系统
遗传算法优化参数,自动生成最优的隶属度函数和控制规则,通过程序写入模糊控制器。图3 为基于GA 优化的自适应模糊控制器的仿真模型。
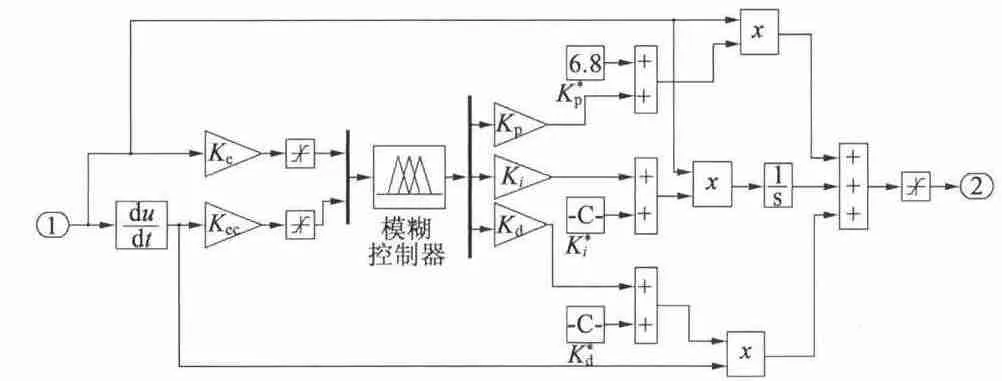
图3 模糊自适应PID 控制模块仿真图
3 仿真结果及分析
GA 参数:种群大小等于30,进化代数选取100。变异概率pm=0. 01,交叉概率pc=0. 7。w1=0.999,w2=0.001,w3=2,w4=100。
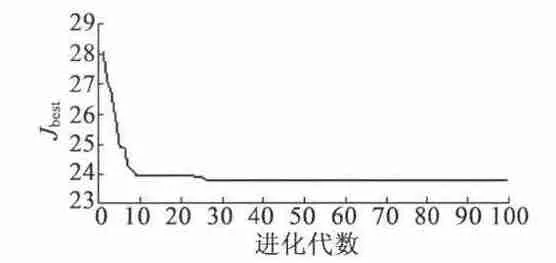
图4 目标函数J 的优化过程
图4 为目标函数的优化过程。随着进化过程的进行,目标函数逐渐减小,当种群进化到第26 代时,目标函数达到最优解。
图5 为采用GA 优化后的控制器阶跃响应图,由图5 可知,采用该控制器的控制系统没有超调,响应迅速并能较快恢复稳定。
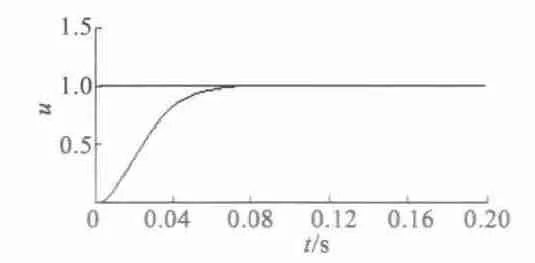
图5 GA 优化后模糊PID 控制的阶跃响应曲线
经遗传算法优化后的隶属度函数及模糊规则用于Fuzzy 控制器,选取Mamaddni 作为模糊化方法,反模糊化使用面积中心法,将控制器用于MATLAB双闭环控制系统中进行仿真。
电机参数:额定电压U =12 V,极对数p =4,定子电阻R=0.65 Ω,有效电感L =0.24 ×10-3H,转动惯量J=2.1 ×10-5kg·m2,摩擦系数1 ×10-5,仿真时长0.2 s。
在变换转速试验中,系统无负载起动,起始n =600 r/min,t=0.1 s 时n =1 000r/min。电机转速对比仿真曲线如下。
图6 为转速对比曲线,图7 为转速对比曲线的局部放大图。仿真结果表明,基于GA 优化后的控制器,系统上升时间短,无超调,稳态误差小。
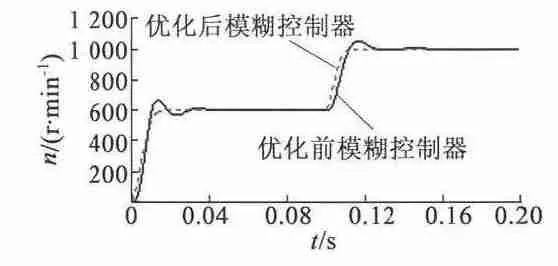
图6 转速对比波形
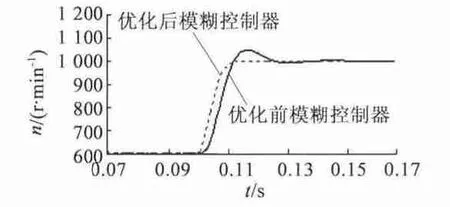
图7 转速响应对比曲线局部放大图
改变负载试验中,在0.15 s 时施加负载Tl=20×10-3N·m,得到转速对比波形如图8 所示,ia波形、ea波形和Te波形如图9 所示。
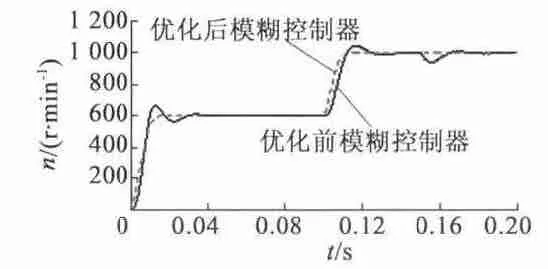
图8 施加负载的转速对比波形
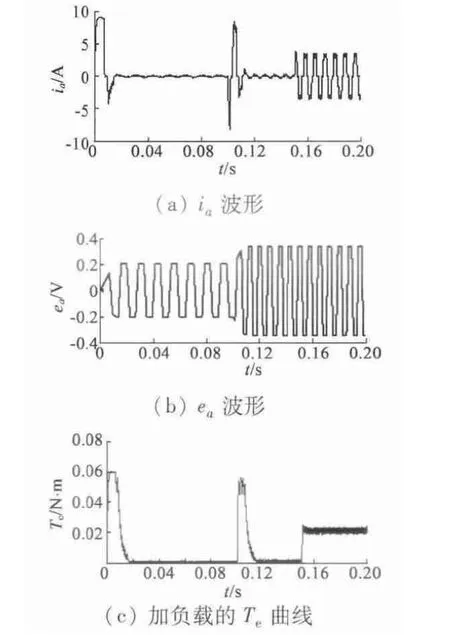
图9 ia,ea,Te 波形
从图8 可以看出,经遗传算法优化后的控制器,在改变负载时扰动小,并很快又达到额定转速,具有较好的系统抗干扰性和鲁棒性。
从图9(a)可以看出,在空载运行时,相电流很快到达稳定,0.15 s 施加负载后,为增大电磁转矩,带动外界负载,ia增大。图9(b)显示,系统空载时,ea为理想梯形波,其顶部约为120°,0.15 s 时改变Te,幅值略微变大。从图9(c)可以看出,空载运行时,达到最大的起动转矩,变换速度时引起转矩脉动并迅速恢复稳定。0.15 s 时加入负载运行,转矩迅速增大并保持稳定,整个过程中转矩脉动较小。
4 结 语
本文提出基于遗传优化机制的自适应模糊控制器设计方法,并用于BLDCM 的控制系统。这种设计方法能够自动生成最优的隶属度函数以及相应的模糊控制规则集合。MATLAB 仿真表明,采用遗传算法优化自适应Fuzzy-PID 控制器的BLDCM 控制系统具有响应迅速、超调较小、无稳态误差等优点。尤其在负载发生变化时,系统能很快再次稳定下来,具有较好的适应能力和鲁棒性。
[1] 蒋旭益,王立标.基于自适应模糊PID 无刷直流电机控制研究[J].科学技术与工程,2011,11(27):6720 -6723.
[2] 张小莉,张波.无刷直流电机自适应模糊控制系统建模与仿真[J].机电一体化,2011,17(4):28 -32.
[3] 孙佃升,白连平.模糊自适应PID 控制器在无刷直流电机控制系统中的应用[J].电气传动,2009,39(10):63 -66.
[4] 孙霞.基于遗传优化的无刷直流电机模糊控制的研究[J].煤矿机械,2011,32(10):104 -106.
[5] 范冰洁,李玉忍,陈永禄.基于遗传算法的无刷直流电机控制参数优化[J].计算机仿真,2009,26(8):188 -192.
[6] JAMALUDIN J,RAHIM N A,HEW W P.Development of a selftuning fuzzy logic controller for intelligent control of elevator systems[J].Engineering Applications of Artificial Intelligence,2009,(22):1167 -1178.
[7] 邵克勇,张鸿雁. 一种基于GA 的模糊控制规则优化新方法[J].化工自动化及仪表,2011,38(3):261 -264.
[8] 王锋,张国煊,张怀相. 模糊隶属度函数的遗传优化[J]. 杭州电子科技大学学报,2009,29(4):34 -37.
[9] 刘镇,李程远.用遗传算法优化模糊控制规则[J].贵州工业大学学报,2009,28(5):7 -11.
[10] 杨玺.基于遗传算法的模糊控制器规则优化[J].电气传动自动化,2010,32(5):41 -44.
[11] 董娇玲.基于遗传算法优化可调整控制规则的模糊控制[J].计算机应用与软件,2010,27(11):203 -205.
