多项式直接拟合在铂电阻高精度测温中的研究

吴志祥 ，周祥才 ，黄 亮 ，陈 功

（1.常州工学院 电子信息与电气工程学院，常州213002；2.常州工学院 光电工程学院，常州213002）

温度是表征物体冷热程度的物理量，是工业生产和科学实验中一个非常重要的参数。铂电阻以其性能稳定、测温范围宽、易标定及互换性好等特点，在温度测量中得到了广泛应用。国际温标ITS－90中还规定，将特殊构造的铂电阻作为-259℃～961.78℃标准温度计来使用。

因铂电阻的电阻值与温度之间存在非线性关系，复现温度时需要进行非线性运算，即“非线性校正”。非线性运算的基础是分度函数或分度表[1-3]，是高精度测温不可缺少的环节，方法多样。应用牛顿迭代法对铂电阻分度函数求解，二次迭代后即可获得满意的精度[4]，但迭代运算时间长，占用内存多。采用神经网络法对0℃～600℃测温范围分六段进行3次多项式拟合，误差小于0.02℃水平[5]。通过根号运算的解析式由电阻值可求解温度值[6]。对称函数非线性法[7]，在0℃～150℃范围内，误差≤0.02℃。应用最小二次法，获得了48℃～50℃范围内，误差≤0.05℃[8]。以及样条插值法[9-10]等。采用非平衡电桥非线性校正方法[11]，则增加了电路复杂性。

高精度测控温，通常为智能式数字仪表。其核心单元通常为单字节8位单片机。因此，研究铂电阻与温度值之间的简易直接算法且占用内存少，颇有价值。

1 铂电阻（PT100）非线性特性

Pt10、Pt100及Pt1000三种铂电阻中，Pt100为最常用温度复现元件。

在0℃～850℃范围内，铂电阻与温度的关系为

式中：a＝3.90802×10－3/℃；b＝－5.80195×10－7/℃；R（100℃）/R（0℃）＝1.38500。因式（1）表达的是温度与电阻值的关系，所以由电阻值求温度值是求逆的过程。

设温度上限量程tF对应的电阻值为RF，量程内温度与电阻值为线性化，则非线性误差为

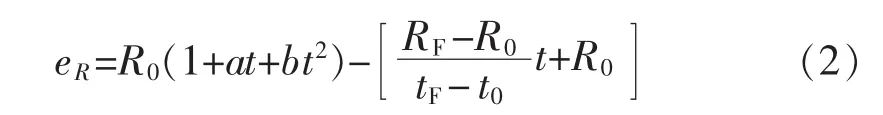
对式（2）求导，并令为 0：

整理得：

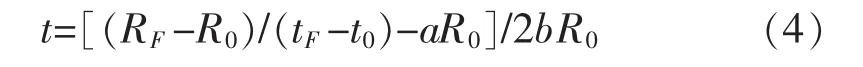
对应 0～650℃、0～850℃温区，非线性误差最大温度值点与电阻值分别为325℃/6.127 Ω与425℃/10.478 Ω，见图1所示。折合非线性误差约为27℃。

2 最小二乘法与权函数

离散数据点（xi，yi）（i=0，1，2，……，m），期望构造近似函数曲线S（x），描述这组数据的内在规律。即选取适当的函数类（集合）

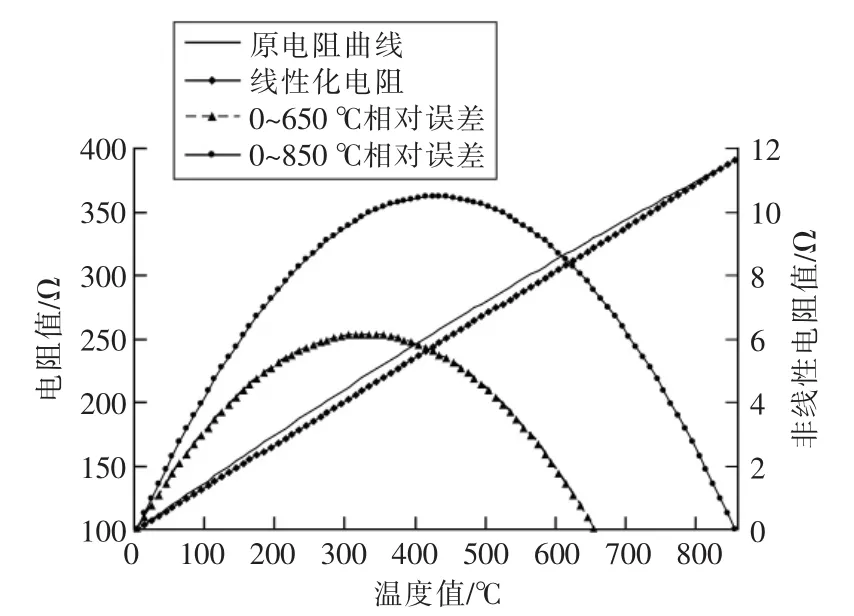
图1 0～650℃、0～850℃非线性误差分布Fig.1 Non-linear errors distribution diagram within the range of 0～650℃ and 0～850℃

φ0，φ1，φ2，……，φn，是［a，b］上 n+1 个线性无关的连续函数。寻求一个函数

使 S*（x）与 y=f（x）在上述 m+1 个点上的偏差（残差）

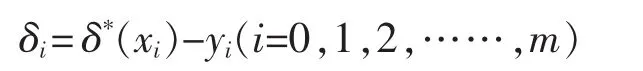
满足

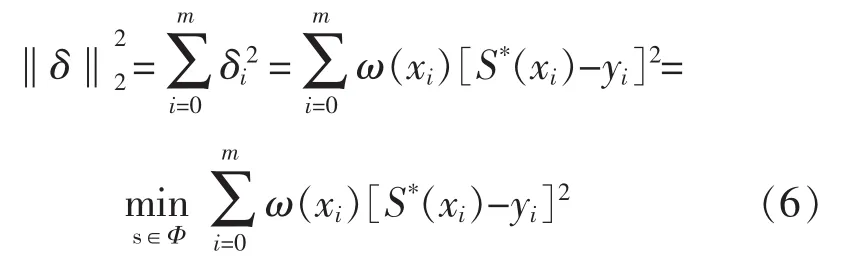
最小二乘法追求“平方差（残差平方和）”最小。曲线拟合时，按其形态可选择复合函数、增长函数、对数函数、指数函数或逻辑函数等本质线性模型进行。但在程序编译时，仍然采用泰勒级数等方法展开为多项式，故，惟有多项式最适用是程序运算。

多项式拟合时，提高多项式次数能改善拟合效果，但将导致方程病态。如采用分段拟合处理，可采用移动最小二乘法 MLS （moving least square）[13]提高拟合精度。

将式（1）按一定温度值间隔点绘制t-R曲线，再对曲线进行R-t拟合。为方便程序运算，采用按温区段进行拟合。考虑最大限度地逼近原函数曲线，或误差分布伴随原曲线呈对称性，先令权函数ω（x）为“1”的定常数进行拟合。然后观察误差分布情况，调整权函数中对应节点的权重，重新拟合，如此反复，直至误差分布接近对称时结束。

3 铂电阻多项式拟合

多项式可写成乘积—相加的循环运算，占用内存小，运算速度快。

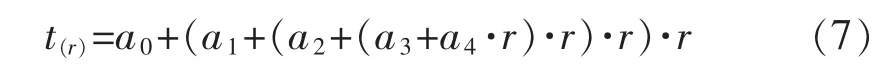
式中：t（r）为温度值；r为实测铂电阻值。 一旦测得了铂电阻值，便可使用式（6）直接计算出对应温度值。

铂电阻测温，通常把0～650℃称为标准温区段，650℃～850℃称为扩展区段，而0～850℃称为全局区段。为此，在本拟合中分三组进行拟合计算。

依据前述原理，利用数学计算工具软件Matlab等，可求得多项式（7）各系数，如表1所示。

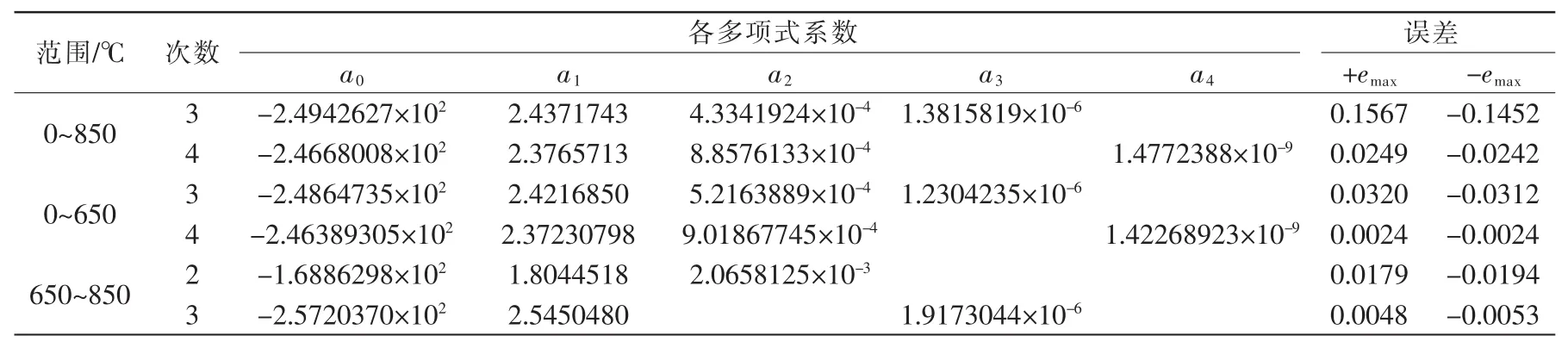
表1 正温区三区段范围3次、4次多项式系数表Tab.1 Cubic polynomial and quartic polynomial graph within three temperature ranges

全局区段，三次多项式最大绝对值误差为0.1567℃，已满足现场温控之需要。四次多项式拟合后最大绝对值误差为0.0249℃，可确保0.1℃精度的精确测温之需。

标准区段，三次、四次多项式拟合最大绝对值误差分别为0.0320℃与0.0024℃。四次多项式拟合可确保0.005℃计量测温要求。

对于扩展区段，二次、三次多项式拟合最大绝对值误差分别为0.0194℃与0.0053℃。

表1显示，各区段三次多项式已能满足绝大多数工程测温精度需要。对于计量要求，可采用四次多项式运算。表1中扩展区段还显示，采用最小二乘法拟合时，同样的阶数，区段范围越小，精度越高。

为了更清楚地显示拟合效果，显示全局区段及标准区段的误差分布情况，分别见图2及图3所示。

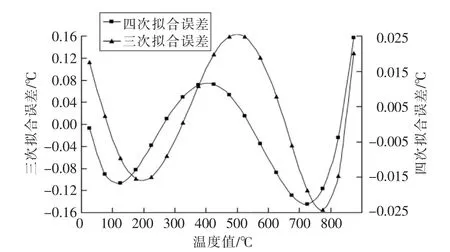
图2 0～850℃温区三次、四次拟合误差分布Fig.2 Error distribution of cubic and quartic fitting within the range of 0～850 ℃

图3 0～650℃温区三次、四次拟合误差分布Fig.3 Error distribution of cubic and quartic fitting within the range of 0～650 ℃

4 C语言与运算速度

以单片机或SOC（system on chip）为核心的智能仪器仪表中，现今广泛采用C语言编程。C语言自身并无精度标准。实型变量分为单精度（float型）、双精度（double 型）及长双精度（long double型）3类。其中float型占用内存4个字节，运算速度最快。且SOC系统中，考虑内存较小的原因，几乎全部采用float型运算。

为了方便起见，仍以标准版8051单片机12 MHz振荡频率为例，在Keil平台用C语言验算，对0～650℃的四次多项式拟合，将表1中各系数代入式（7）得具体算式（8），运算结果与EXCEL运算结果，如表2所示。

t（r）=-246.38931+（2.3723080+（9.0186775×10-4+

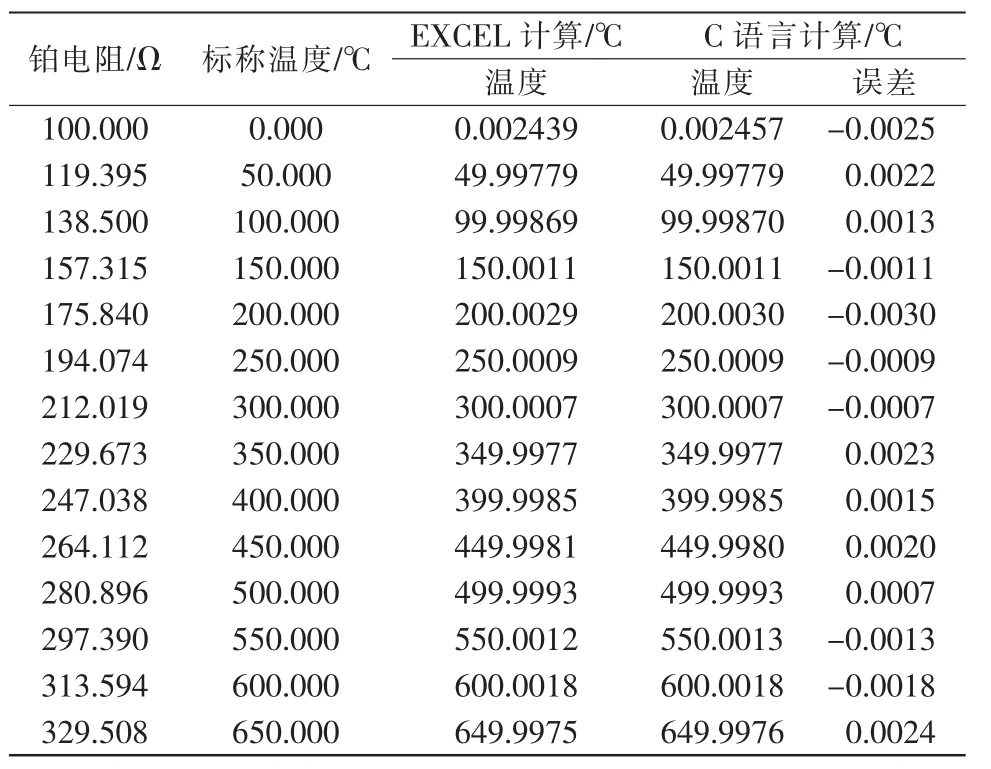
表2 C语言与EXCEL计算比较Tab.2 C language and EXCEL calculation comparison

电 阻 值 为 100.000 Ω、212.019 Ω 及 329.508 Ω时的程序拟合运算时间，分别为1470MT（Machine Period）、1487MT 和 1488MT。 可见式（7）运算的快速性。

表2还显示了Keli C运算的正确性。

5 结语

这里对铂电阻非线性函数求逆运算的常见方法及存在问题简要总结后，采用最小二乘法调整权函数之方法，对铂电阻正温区按3种区段，进行了拟合运算，得到了三次、四次多项式系数，并给出了拟合运算误差分布图。在0～650℃温区范围内，应用四次多项式拟合运算，最大误差仅为±0.003℃。多项式拟合运算，算式简单明了，占用内存小，运算速度快，特别适用于采用C语言编程的单片机或SOC中。C语言采用单精度实型变量运算后的精度与速度，进一步证实多项式拟合的优越性。文中给出的多项式系数，可直接用于铂电阻测温需要。多项式拟合方法亦可使用于热电偶测温中。

[1] Bentley，Robin E.Handbook of Temperature Measurement[M].CSIRO，2000.

[2] L Michalski，K Eckersdorf，J Kucharski，J，ea al.Temperature Measurement Second Edition[M].LUDWIG MICHALSKI，Lodska Polytechnic，Poland Published：March 2001.

[3] 李吉林.常用热电偶热电阻分度表-ITS-90[M]北京：中国计量出版社，2010.

[4] 杨永竹.铂电阻高精度非线性校正及其在智能仪表中的实现[J].仪表技术与传感器，2000（8）：44-46.

[5] 王小华，何怡刚.铂电阻Pt100特性数学模型[J].传感器技术，2003，22（10）：33-34.

[6] 杨平，李志武.常用热电阻的温度—阻值变换的解析计算[J].传感器技术，2002，21（1）：38-41.

[7] 王勇，王晓东.高精度铂电阻测温非线性校正方法[J].测控技术，2004，23（7）：75-76.

[8] 易先军，文小玲，刘翠梅.基于铂电阻的温度高精度测量研究[J].传感器与系统，2009，28（1）：49-51.

[9] 刘少强，黄惟一.基于插值计算与优化的铂电阻非线性校正方法[J].仪器仪表学报，2003，24（2）：215-217.

[10]姬建伟，李平，宋家友.铂电阻高精度测量和非线性校正的研究[J].微型计算机信息，2007，23（5）：164-165.

[11]任殿慧，周巧娣，章雪挺，等.一种铂电阻测温电路的非线性校正方法[J].电子器件，2010，33（5）：603-606.

[12]谢伟松.数值分析[M]天津：天津大学出版社，2000.

[13]张淮清，俞集辉.线路电磁场测量数据的移动最小二乘拟合处理[J].高压电技术，2010，36（3）：661-665. ■