一种基于支持向量的二进制粒子群网络故障特征选择算法

夏爱民 温祥西 张宏志

(1.后勤学院研究生管理大队北京 100036；2.空军工程大学空管领航学院陕西西安 710077；3.61139部队北京 100091)

一种基于支持向量的二进制粒子群网络故障特征选择算法

夏爱民1温祥西2张宏志3

(1.后勤学院研究生管理大队北京 100036；2.空军工程大学空管领航学院陕西西安 710077；3.61139部队北京 100091)

网络故障诊断中大量无关或冗余的特征会降低诊断的精度，需要对初始特征进行选择。Wrapper模式特征选择方法分类算法计算量大，为了降低计算量，本文提出了基于支持向量的二进制粒子群(SVB-BPSO)的故障特征选择方法。该算法以SVM为分类器，首先通过对所有样本的SVM训练选出SV集，在封装的分类训练中仅使用SV集，然后采用异类支持向量之间的平均距离作为SVM的参数进行训练，最后根据分类结果，利用BPSO在特征空间中进行全局搜索选出最优特征集。在DARPA数据集上的实验表明本文提出的方法能够降低封装模式特征选择的计算量且获得了较高的分类精度以及较明显的降维效果。

网络故障 特征选择 二进制粒子群 支持向量

1 引言

网络故障的诊断本质上是一个模式识别问题，现有的网络故障诊断方法往往直接将收集的网络故障数据送入分类器进行训练和识别。但是原始特征中往往含有冗余特征甚至噪声特征，这些冗余特征不仅会增加训练的复杂度，还可能降低分类精度。在最终的诊断应用中，还会影响诊断速度。可见从采集的初始故障集中选出最能代表故障特性的稳定特征子集对诊断具有十分重要的意义。

近年来，特征选择问题得到了广泛的研究，根据是否依赖机器学习算法，特征选择算法可以分为两大类：一类为Wrapper型算法，另一类为Filter型算法[1-3]。Filter型特征选择算法独立于机器学习算法，计算代价小，效率高但效果一般，典型的算法包括采用类间距离作为亲和度函数的AICSA算法[4]；而Wrapper型特征选择算法则需要依赖某种或多种机器学习算法，计算代价大，效率低但选择效果好，例如文献[5-6]提出的BPSO-SVM特征选择算法。本文选择Wrapper型算法，Wrapper首先要考虑的是采用哪种机器学习方法进行分类。支持向量机（SVM）建立在结构风险最小化原则基础之上，具有很强的学习能力和泛化性能，本文选择SVM作为Wrapper的机器学习算法。但是，前面已经提到Wrapper最大的缺点是计算代价特别高：BPSO-SVM需要进行大量的SVM训练，阻碍了这些方法的实用性。因此，如何降低Wrapper型特征选择的计算代价成为亟待解决的问题。而这些计算主要是由SVM训练引起，需要从SVM训练过程中去寻求解决方法。

本文分析了典型的基于SVM的Wrapper型特征选择算法，从提高训练参数的优化速度以及减少训练规模这两个方面降低整个选择算法的计算代价。并结合二进制粒子群（BPSO）算法寻找最优的特征组合，提出一种新颖的基于支持向量的二进制粒子群（SVB-BPSO）特征选择算法。SVB-BPSO仅使用支持向量集作为BPSO寻优时SVM的训练集，且在参数寻优时通过固定RBF核带宽仅寻找最优的惩罚因子的方式快速确定最终的最优分类精度，降低了整个选择过程的计算代价。

2 相关研究工作分析

本节分析现有的典型特征选择算法的计算代价，从中找出减少计算量的途径和方法。首先分析BPSO-SVM，它是一种典型的Wrapper特征选择模型。特征选择实际上是一个组合优化问题，可以采用一些启发式的搜索算法求解，关键是如何设置优化目标。在该算法中，优化的目标函数综合考虑分类准确性（accuracy）和特征维数（feature_dim）：

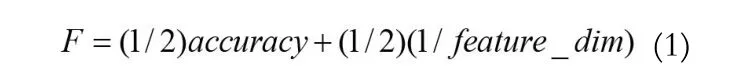
其中，SVM的accuracy是通过交叉验证的方式得到的。计算accuracy过程中，如文献[5]所提的采用5折交叉验证，则对于每个选取的参数均需要进行5次SVM训练才能确定最终的accuracy；考虑交叉验证获得最优的参数过程，无论采用网格搜索还是启发式算法都需进行多次SVM训练。若不考虑参数的寻优，如文献[6]中，采用LIBSVM的缺省设置，则得到的accuracy无法保证是最佳的，也就影响了目标函数的准确性。因此，如果能够快速找到最优的SVM训练参数将能降低算法的计算量。

另一个方面，SVM的训练过程是一个求解二次规划的过程，它的计算代价与训练样本的个数相关。在不降低分类准确度的情况下减少参与训练的样本个数也能够降低算法的计算量。文献[7]提出一种基于SVM的递归特征约简算法（SVM-recursive feature elimination，SVM-RFE），通过定义的评价函数来评估每一个特征维对分类的敏感度（贡献度），最终为每个特征按照敏感度进行排序，最终通过排序表定义若干个嵌套的特征子集训练并评估这些子集的优劣，选出最优的特征。它的评价函数为：

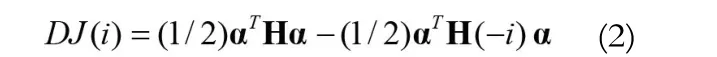
3 SVB-BPSO算法描述

通过第二部分的分析，本文提出的SVB-BPSO特征选择算法框图如图1所示。首先对训练样本进行SVM训练（包括通过5折交叉进行参数寻优），获得最终的SV集；对选择的SV集通过BPSO算法进行寻优找到最终的最优特征集；最后将测试样本代入最优特征集中进行测试得到最终的分类结果。图中，New SV集代表的是当前粒子编码对应的SV集。

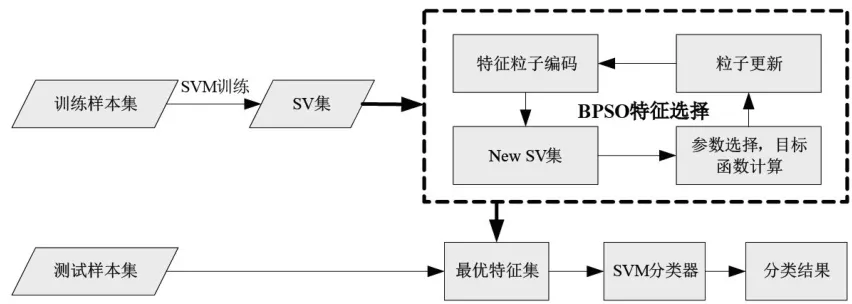
图1 SVB-BPSO特征选择算法框图

下面就框图中的参数寻优以及BPSO特征选择进行详细介绍。

3.1 SVM参数快速确定

SVM训练需要确定的参数包括核参数和惩罚因子，这些参数的选取对最终的分类结果会产生较大的影响进而影响特征选择结果[9-10]。在文献[6]中并未考虑SVM训练参数的寻优问题，虽然SVM具有较大的最优区域，但是仅通过简单设定往往不是最优的参数。SVM的训练参数的寻优问题是一直是SVM学习中的一个热点问题，效果比较好的包括交叉验证和网格搜索以及一些智能搜索算法相结合的方法，但是这些方法需要大量的SVM训练。快速找到一个较优的参数能够较大的降低算法的计算量。常用的核函数包括线性核函数、多项式核函数（Polynomial Function）、径向基核函数（Radial Basic Funtion，RBF）以及感知核函数（Sigmoid Function）。文献[11]评估结果显示，径向基核函数（Radial Basic Function，RBF）的无穷维映射特性使之具有很强的学习能力且只需优化核带宽一个参数，故本文选择RBF作为SVM的核函数。下面对RBF核函数进行分析，首先给出RBF核函数的数学表达式：

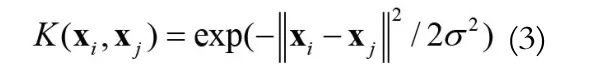
图2显示了不同核宽度值对RBF核函数的影响。

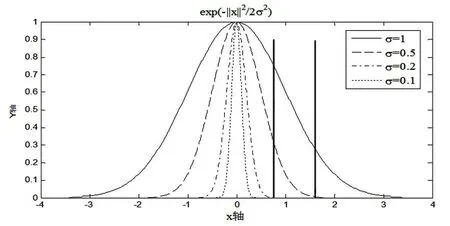
图2 不同参数的径向基核函数

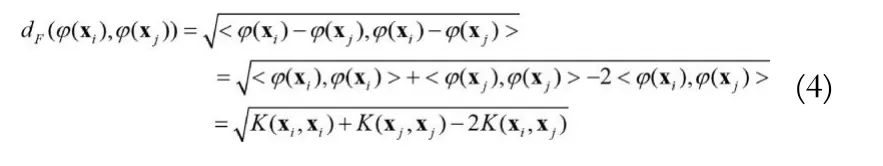
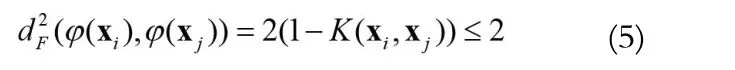
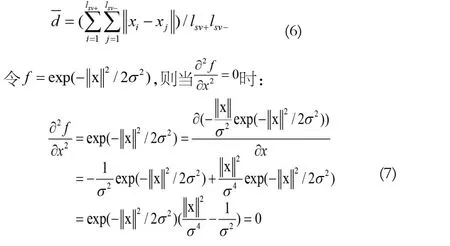
3.2 BPSO算法

粒子群算法是Kennedy和Eberhart模仿鸟类群体行为的智能优化算法，可解决连续函数的优化问题[12]。在算法中，群体中的每个粒子都是一个潜在的解，通过学习历史中自身的最优位置Pb和群体最优位置Pg来更新位置和速度，并根据粒子的位置计算适应度函数来判断解的优劣，不断迭代找到最优解。

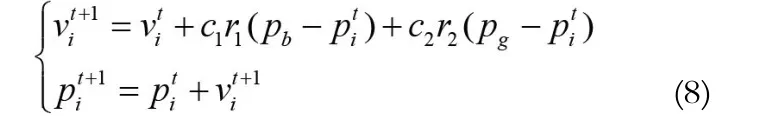
其中，t为迭代次数，c1和c2为学习因子，r1和r2为[0,1]之间的随机数。

为解决粒子群在离散问题中的应用，Kennedy和Eberhart又在标准粒子群的基础之上提出了二进制粒子群优化算法[10]。其原理和速度的更新方式不变，只是将粒子位置的每一维分量限制为0或1，并根据速度的sigmoid函数变换来控制粒子的位置更新：

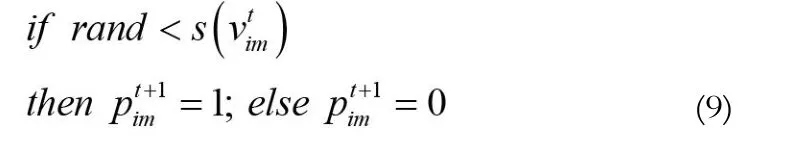
本文提出的SV-BPSO算法采用wrapper特征选择模型，利用BPSO的自动寻优能力在特征空间中进行全局搜索，得到不同特征组合。根据SVM分类结果判断这些特征组合的分类性能，并不断更新选取的特征集，直至搜索到取得最佳分类结果的特征组合。与神经网络、遗传算法等优化算法相比，PSO具有所需确定的参数较少，收敛速度更快等优点；与顺序选择算法等常用特征选择方法相比，PSO不易陷入局部极值，能得到全局最优解。

3.3 基于SVB-BPSO的特征选择

如果将整个特征空间看作解空间，不同特征组合看作解空间中不同位置处的粒子，粒子中各位置分量取值对应特征组合中各特征分量的状态。在BPSO寻优中，首先需要根据问题对候选解进行编码：把每一个特征定义为粒子的二进制变量，粒子空间维数D由原始特征集维数决定。如果第i位为1，那么第i个特征就被选中，否则这个特征就被丢弃。

BPSO算法中，某个粒子的位置矢量决定了某种特征子集的组合方式，而整个群体最优点Pg确定了系统的最优特征组合，适应度函数Fit指导粒子群搜索方向。特性选择的目的是使用尽可能少的特征得到相同或更优的分类性能，因此，适应度函数需要综合考虑分类准确性(accuracy)和特征维数(feature_dim)。式(1)给出的适应度函数将这两部分视作同等重要，但是当accuracy较小时（如0.6），若feature_dim为1，则F=0.3+0.5=0.8，此时的F高于当accuracy达到1而feature_dim为2（F=0.5+0.25=0.75），我们显然不能认为第一种情况好于第二种情况。其它文献给出的目标函数同样没有很好的解决这两部分的权值关系。若原始样本集训练获得的分类精度（accuracy_1），在以下假设的前提下：

假设1：经过特征选择后获得的最终accuracy同accuracy_1相差不大。

从文献[5-8]中对大量数据集的实验可以看出经过特征选择得到的最终accuracy一般略高于或者略低于accuracy_1，这说明假设是可以成立的。另外，考虑在目标函数中，我们更注重最终的accuracy，且认为当feature_dim对目标函数的影响较accuracy低一个数量级时由accuracy主导目标函数值。我们给出的最终的目标函数为：

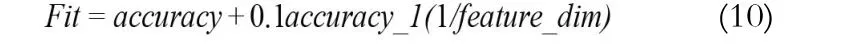
结合3.2，给出BPSO进行特征选择的步骤：输入：初始样本集为类别数，lsv为支持向量个数），种群规模np，最大迭代次数iter，适应度函数Fit，阈值Th。

步骤1：初始化粒子位置和速度，设定粒子规模np，最小和最大飞行速度vmin和vmax，最大迭代次数iter，适应度函数阈值Th，计算每个粒子适应度函数Fit，初始化pb、pg以及迭代次数n=1。

根据式(8)和(9)更新每个粒子的速度vid和位置xid

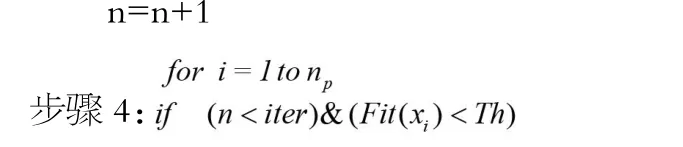
返回2

else停止迭代，输出群体最佳位置Pg和Fit(Pg)。

步骤5：选择当前种群中最优个体Pg中为1的基因位对应S中的样本特征，构成约简样本集

4 实验与分析

4.1 数据处理

目前网络中各种攻击事件和病毒越来越多，导致网络中产生大量的"软故障"，如网络服务异常、操作系统崩溃、链路拥塞甚至中断等。本文选择了DARPA评估数据集[13]，以攻击下的网络状态模拟网络故障。该数据集包含四类网络攻击，分别是DoS、Probe、R2L和U2R，每条记录均有41个特征值。为了确保数据的普适性，从原始数据集中以等间隔采集法选取训练集样本和测试样本，具体情况如表1所示：

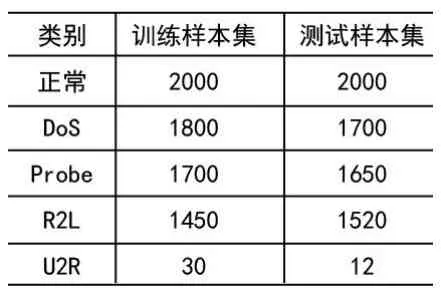
表1 实验样本集结构

此外样本特征属性值之间的不同度量，使得样本向量在计算距离时取值范围偏大的属性占据了主导地位，大大弱化了取值范围偏小的特征的贡献，无法正确反映样本间的真实差异。设特征集合中的第i个特征的最大最小值分别为，则通过式(12)的归一化处理将训练和测试集中的样本特征值映射到[0,1]区间：

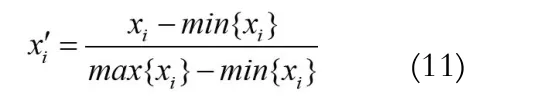
4.2 实验结果与分析

对以上经过预处理的样本数据集，分别使用文献[4]提出的AICSA方法、文献[5]提出的BPSO-SVM方法和文献[6]的BPSO-SVM方法，文献[7]的SVM-RFE、文献[8]的SV-RFE以及本文的SVB-BPSO方法进行特征选择，并对测试样本进行分类，分别比较选择的时间、得到的特征维数、测试的诊断精度。其中，BPSO的种群规模取20，最大迭代次数取100，SVM的训练工具采用LIBSVM[14]（注意：LIBSVM中的参数核函数的表示形式为：，这里即为训练中的参数g，其表达式与式(3)不同，因此设置参数时）。得到是实验结果如表2所示：

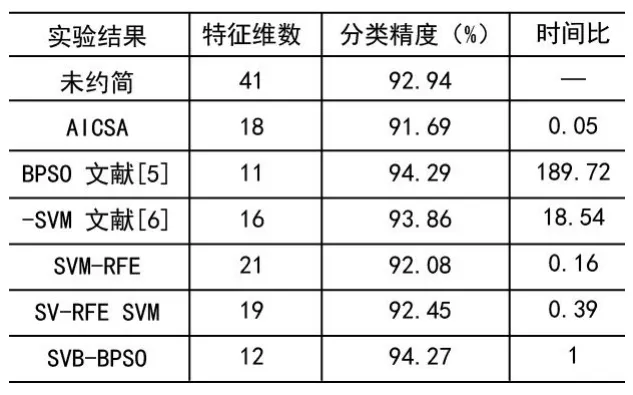
表2 实验结果

其中，时间比是其它方法同本文方法所用时间的比值。从实验结果可以发现基于Filter思想的AICSA特征选择方法能够获得最低的选择时间，远远快于其它算法。这是因为在Filter的选择中仅分析数据之间的关系，不考虑分类，但是它获得的分类精度也低于其它方法。经过文献[5]提出的BPSO-SVM方法选择出来的特征得到了最高的分类精度，但是它所花的时间远远高于其它方法，这主要是因为它在训练中采用5折交叉验证方式确定参数并训练，这中间需要进行大量的SVM训练，因此它需要较长的时间。另外由于它考虑了训练参数且训练使用的是所有数据，它最终得到的选择结果也是最好的。文献[6]中并未考虑参数设置问题，本文由于在前期进行了归一化处理，在使用缺省设置参数时能够获得较好的训练效果。在其它一些数据集实验时还是表现出了训练参数对最终提取结果还是有较大影响的。在训练时间上，即使不需要参数设置，但是每次计算目标函数过程中的训练集仍为所有数据，因此它的寻优时间高于本文方法。SVM-RFE通过SVM得到Lagrange乘数，通过式(2)判断每一维的分类敏感性，式(2)的计算不涉及SVM训练，因此它的寻优时间较短。SV-RFE SVM方法减少了参与寻优的样本，但是每次均要进行SVM训练计算判别函数，时间上较SVM-RFE略长，但是这两种方法得到的最终分类精度低于本文方法以及文献[5]中的BPSO-SVM，且选择的特征维数较多。实验结果很明显的体现出本文方法的优势：用了一个较短的寻优时间获得了相对较高的分类精度以及较明显的维数降低效果。

5 结束语

特征选择在网络故障诊断领域能够提高诊断的精度和速度，作为目前特征提取效果较好的Wrapper模式选择算法由于计算目标函数时需要进行分类训练，带来大量的计算。为了降低Wrapper模式中的计算量，本文从SVM分类器的训练出发，通过对SVM训练参数确定以及参与训练样本个数两个方面考虑降低SVM的训练代价。并对分类结果和选择出的样本维数的综合考虑，利用BPSO在特征空间中进行全局搜索选出最优特征集。最后，在DARPA数据集上的特征提取实验表明本文提出的方法能够折中的获得较优的分类精度较好的降维效果以及较低的运算代价。本文提出的方法能够为网络故障诊断中的特征选择问题提供一种新的较优的途径。

[1]Zhu Z,Ong Y,Dash M.Wrapper-filter feature selection algorithm using a memetic framework[J].IEEE Transactions on Systems,Man,and Cybernetics-Part B:Cybernetics, 2007,37(1):70-76.

[2]Zhao Mingyuan,Fu Chong,Ji Luping,Tang Ke,Zhou Mingtian.Feature selection and parameter optimization for support vector machines:A new approach based on genetic algorithm with feature chromosomes[J].Expert Systems with Applications 2011,38(5):5197-5204.

[3]Kim S.,Oommen B.On using prototype reduction scheme to optimize kernel-based Fisher discriminant analysis.IEEETransactions on Systems,Man,and Cybernetics-Part B: Cybernetics,2008,38(2):564-570.

[4]Zhang Li,Meng Xiangru,Wu Weijia,Zhou Hua.Network Fault Feature Selection Based on Adaptive Immune Clonal Selection Algorithm[A].2009 International Joint Conference on Computation Sciences and Optimization[C].Hainan, China:2009,969-973.

[5]潘泓,李晓兵,金立左,夏良正.一种基于二值粒子群优化和支持向量机的目标检测算法[J].电子与信息学报,2011,33 (1):117-121.

[6]乔立岩,彭喜元,彭宇.基于微粒群算法和支持向量机的特征子集选择方法[J].电子学报,2006,34(3):496-498.

[7]Guyon,I.,Weston,J.,Barnhill,S.,Vapnik,V..Gene selection for cancer classification using support vector machines[J].Machine Learning,2012,46(1/3):389-422.

[8]Eunseog Youn,Lars Koenig,Myong K.Jeong,Seung H. Baek.Support vector-based feature selection using Fisher's linear discriminant and Support Vector Machine[J].Expert Systems with Applications 2010,37(9):6148-6156.

[9]Vapnik.An Overview of Statistical Learning Theory[J].IEEE Transaction on Neural Network,2009,10(5):998-999.

[10]Chapelle O,Vapnik V,Bousquet O,et al.Choosing multiple parameters for support vector machine[J].Machine Learning,2012,46:131-159.

[11]王泳，胡包钢.应用统计方法综合评估核函数分类能力的研究[J].计算机学报,2008,31(6):942-952.

[12]Kennedy J,Eberhart R C,Shi Y H.Swarm intelligence[M].北京:人民邮电出版社,2009.

[13]University of California Irvine.UCI KDD Archive [DB/OL].http://kdd.ics.uci.edu/

[14]Chih-Chung Chang,Chih-Jen Lin.LIBSVM:A library for support vector machines[EB/OL].http://www.csie. ntu.edu.tw/～cjlin/libsvm.

A Support Vector Based Binary Particle Swarm Optimization Feature Selection Algorithm

XIA Ai-min1，WEN Xiang-xi2，ZhANG Hong-zhi3
（1.Graduate Management Unit of The Logistics College,PLA,Beijing 100036,China; 2.Institute of Air Traffic Control and Navigation,Air Force Engineering University,Xi'an Shanxi 710077,China；3.61139 PLA Troops,Beijing 100091,China）

In network fault diagnosis,many irrelevant and redundant features lessen the performance of diagnosis,feature selection is introduced on this condition.The wrapper feature selection algorithms get large calculation cost,a support vector based binary particle swarm optimization(SVB-BPSO)feature selection algorithm was proposed in this paper.The support vectors(SVs)are selected from the whole datasets by SVM training,the following wrapper classification focus only on these SVs.The training parameter is decided by average distance between different class SVs.Based on the SVM classifiers,the BPSO is used for searching the whole feature space to find the best feature subset.Experiments on DARPA datasets show the proposed method can reduce the wrapper feature selection's calculation cost while gets good performance on diagnosis accuracy and dimensional decrease.

network fault;feature selection;BPSO;support vector

TP391.4

A

1008-1739（2014）23-68-6

定稿日期：2014-11-12