装备器材保障网络仿真与抗毁性测度

王铁宁，于双双，梁 波

(装甲兵工程学院技术保障工程系，北京100072)

装备保障网络是军事物流的载体，承担着将装备器材从后方仓库或工厂运送到师、旅(团)等战术单位的任务。网络节点包括后方仓库、队属仓库以及各路口、桥梁、港口码头等交通枢纽，节点众多、性质复杂;网络的边包括各等级的公路、铁路以及水路和空运等，距离长短不一，网络流量易受本身通行能力、外部环境的影响。未来战争中，作战双方在战略战术运用上，将更加重视破坏敌方的保障系统，保护己方的保障系统。王宗喜等［1］指出军事物流资源配置要具有战略性、前瞻性，要符合未来战争的实际。文献［2-3］作者在研究企业供应链时发现:考虑设施失效的供应链设计能够明显改善供应链中断时设施的服务效果。因此，装备保障网络在设计阶段应充分考虑其在未来战争中应对网络失效的能力，研究装备保障网络的抗毁性、提高装备保障网络在应急条件下的生存能力，已成为新军事时期的重要课题。

不同学者针对不同的网络(如军事网络［4］、通信网络［5-6］、物流网络［7］等)对抗毁性提出了不同的定义。温巧林等［4］总结了军事通信网络与一般通信网络在抗毁性研究方面的特殊性;刘啸林［5］总结了2种提高抗毁性指标求解效率的方法;谈革新［8］根据国内外的相关文献，将网络抗毁性测度研究总结为抗毁性测度算法的基础阶段、应用阶段和复杂网络抗毁性阶段;Ghashghai等［9］设计了一个混合基因算法，把一个较大的网络分解成由若干个k-树组成的网络。但是截至目前，对于装备器材保障网络的构建与抗毁性仍然没有针对性的研究。

研究装备器材保障网络的抗毁性能问题，可通过仿真方法生成一般意义上的装备保障网络，然后考虑运行在网络中的保障业务，研究其节点、边或者运载工具在遭受外界因素(如自然灾害、敌人火力打击等)影响而发生中断时，依靠网络自身的拓扑结构属性以及应急处理预案，能够维持网络拓扑结构稳定性以及保障业务可持续性的能力。

1 装备器材保障网络的构成仿真

网络由节点和边构成。装备器材保障网络中的节点是器材供应线路的连接之处，也是供应线路的起点和终点。本文将所有的保障实体、交通枢纽以及被保障实体抽象为节点。按照保障任务的属性，将保障网络中的节点分为保障节点、连接节点和需求点3类。

1)保障节点。在装备器材保障网络中，具有器材接收或者发送能力的节点称为保障节点，包括战略保障中心、区域保障中心和群点保障中心。

2)连接节点。在器材保障网络中，所有不具备器材物资接收或者发送能力的节点统称为连接节点，其作用是转运资源，作为中转站而存在，这类节点主要是重要的车站、港口等交通枢纽。

3)需求点。是指器材消耗单位，即部队各级修理单位。

边实质上是装备器材保障网络中抽象的道路交通网络，网络中各节点通过公路、铁路、水路和航线等方式连接到一起，形成保障物资输送的路网载体。

研究网络的性能及其变化，首先应建立相应的网络模型，包括网络的节点、边及其之间的关系。

1．1 装备器材保障网络生成算法

装备器材保障网络的“骨架”是各级保障中心和需求点，它们之间依靠建制保障关系构成骨干网络，是典型的树状结构，最顶层是战略保障中心，最底层是部队需求点，中间是区域保障中心和群点保障中心。该骨干网络反映了保障网络中各主要节点及其之间的关系。同时，装备器材保障网络中除按建制逐级保障外，还有调剂保障和应急保障，这使得保障网络拓扑结构不是完全的树状结构，各节点之间存在网络交叉关系。另外，连接节点属于公共服务类节点，它可以被多条保障链路共用，这也是保障网络呈现网络交叉状的重要原因。

根据以上分析，可将保障网络生成算法分为3个阶段，如图1所示。

?

网络模型生成步骤具体如下。

1)初始化。设战略保障中心、区域保障中心、群点保障中心、需求点、连接节点的数量分别为N1、N2、N3、N4、N5，连接半径为 R 。根据各类节点数量，为每个节点编号，编号规则为:战略保障中心、区域保障中心、群点保障中心、需求点、连接节点分别以L1-、L2-、L3-、L4-、L5-开头，后面为 1到 N 的阿拉伯数字，例如编号L1-1代表第1个战略保障中心。

2)生成骨干网络。(1)将部队需求点、群点保障中心分别看作网络中的服务接受者和服务提供者，建立部队需求点和群点保障中心之间的建制保障关系;(2)将群点保障中心、区域保障中心分别看作网络中的服务接受者和服务提供者，建立群点保障中心和区域保障中心之间的建制保障关系;(3)将区域保障中心、战略保障中心分别看作网络中的服务接受者和服务提供者，建立区域保障中心和战略保障中心之间的建制保障关系。

3)加入连接节点。随机生成N5个连接节点，这些连接节点代表火车站、码头等交通枢纽。

4)网格化。循环每一个连接节点，划定以当前连接节点为圆心、R为半径的圆形区域，在圆形区域内的所有节点(包括战略保障中心、区域保障中心、群点保障中心、部队需求点和连接节点)都与当前连接节点建立连接。

这里假设网络中2个节点只要能够通过连接节点连通，它们之间就可以实现保障与被保障的关系，也就是说，通过网格化，实际上模拟了建制保障、调剂供应保障和越级供应保障。同时，通过调节参数R的大小来控制网络中调剂供应和越级供应保障的范围。

1．2 装备器材保障网络生成仿真

在VS2005平台下，采用C#语言实现本文所设计的网络生成仿真算法，并通过实际的网络生成算例验证该算法的有效性。

1．2．1 仿真数据描述

某区域共有修理单位122个，其中:军械专业45个，装甲39个，工程17个，防化21个。将上述122个修理单位作为器材消耗单位，即部队需求点。由于部队需求点分布较为分散，区域中有1条国道和2条铁路干线，其他主要是省道、县道、乡道。该区域共有58个县市和主要乡镇，构成了该区域交通路网中的枢纽节点。根据上述实际情况确定网络初始参数及其值，如表1所示。

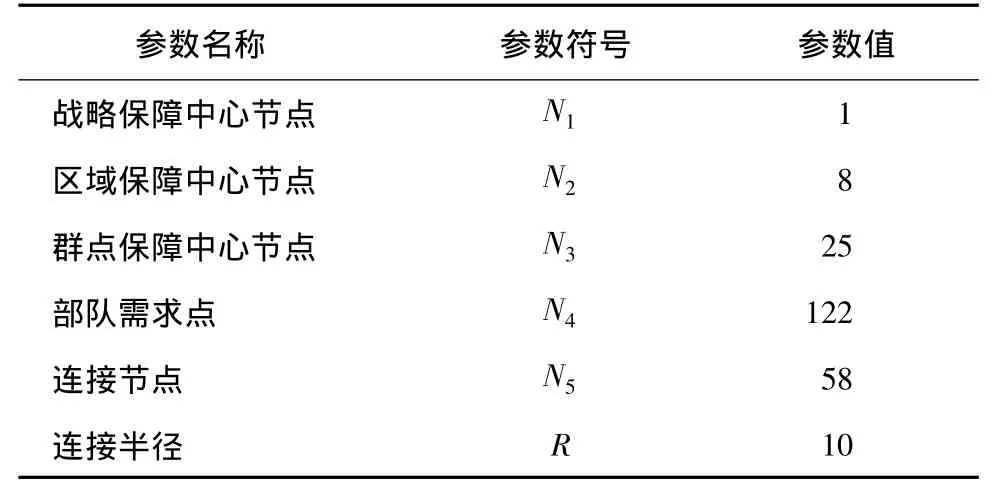
表1 网络参数

1．2．2 网络生成结果

为了使计算机所生成的网络图兼顾真实性与美观性，将战略保障中心、区域保障中心、群点保障中心、部队需求点从里向外排成一个同心圆。连接节点则在整个区域内随机生成，其他节点通过连接节点的位置、连接半径建立路网连接关系。网络的生成过程如图2所示。

图2(a)展示了各级资源点和需求点的分布，其中:最里层的1个点为战略保障中心;第2层的8个点为区域保障中心;第3层的25个点为群点保障中心;最外层的122个点为部队需求点。图2(b)展示了各级节点之间的建制保障关系，是一个典型的树状结构，网络中的边代表保障关系。图2(c)是在图2(a)的基础上随机加入连接节点形成的节点分布图，这些节点代表实际路网中的交通枢纽(如县、市)。图2(d)是在图2(c)的基础上通过连接半径R网格化的结果，模拟了网络中的实际路网以及各节点之间的建制保障、调剂保障、越级保障关系，网络中的节点包括各级资源点、需求点以及连接节点(县、市)，网络中的边代表了实际路网中的交通道路(如公路、铁路)。

图2 网络生成过程

依据装备器材保障网络实际，通过改变表1中的网络参数值，可以仿真生成不同复杂程度的装备器材保障网络图。

2 装备器材保障网络抗毁性测度

抗毁性测度是网络抗毁性大小的衡量指标。网络抗毁性是指网络系统在遭受攻击、故障和意外事件时仍能够及时完成其关键任务的能力［10］。抗毁性可分为静态抗毁性和动态抗毁性2种:静态抗毁性是指按照一定的策略移除网络中的节点或边后研究网络的相关特性，这些失效的节点不会产生“联动”效应，但对网络的整体拓扑结构和网络性能会产生影响;动态抗毁性是从动态的角度来研究网络的相关特性。本文主要研究装备器材保障网络的静态抗毁性。

2．1 装备器材保障网络抗毁性测度研究思路

装备器材保障网络是一种业务网络，网络建设的目的是依托网络上的节点和边完成装备器材的供应功能。同时，装备器材保障网络也是一种物理网络，网络中的各个节点和边都是实际存在的。业务网络是装备器材保障网络的应用层，物理网络是装备器材保障网络的支撑层，业务网络运行在物理网络之上，物理网络对业务网络起支撑作用，物理网络的抗毁性对业务网络有重要影响。装备器材保障网络的层级划分如图3所示。

图3 装备器材保障网络的层级划分

为系统、全面地反映网络的抗毁性本质，本文从物理层抗毁性和业务层抗毁性2个方面研究装备器材保障网络的抗毁性测度。研究物理层抗毁性时，不考虑业务，主要从拓扑结构的角度研究网络自身的一些特性;研究业务层抗毁性时，根据网络的主要职能、部队对保障网络的要求来设计抗毁性测度指标。结构优良的拓扑结构可以提高保障网络的抗毁性能，能适应不同的网络环境:当外部环境较好时，保障网络能以较好的网络效率提供最优的服务;当外部环境恶劣时，保障网络能以较好的鲁棒性保持网络的连通可用性。因此，选择网络效率和网络鲁棒性作为网络拓扑结构抗毁性测度指标。对于保障业务抗毁性指标，选择器材到达率、用户等待时间作为其测度指标，这是因为装备器材保障网络由于其军事特性，对器材的数量、供应时间有很高的要求，特别在战时，这种要求体现得更为明显，而器材到达率和用户等待时间分别从器材保障的数量和时间上刻画了部队需求点对保障网络的要求。

2．2 网络拓扑层抗毁性测度

2．2．1 网络鲁棒性

鲁棒性(Robustness)用来表征控制系统对特性或参数摄动的不敏感性。本文定义装备器材保障网络的鲁棒性(ηR)是用来衡量移除网络中任意一个节点后，网络中剩余节点之间仍能够保持连通能力的平均影响，也就是移除任意节点后，网络中仍然连通的节点对数与网络中未遭受攻击前总节点对数之比的均值，即

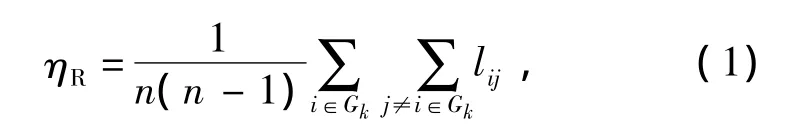
式中:n为节点数目;Gk为移除任意节点后网络中剩余节点的集合;lij为节点i到j的连通参数，即如果节点i到j之间有路径连通，lij=1，否则lij=0。

网络鲁棒性描述了移除节点后网络的连通性，反映了网络被分割的情况，ηR取值范围为［0，1］，其值越小，表明网络中不连通的节点对越多，网络被分割的程度越严重。

2．2．2 网络效率

在高负载或者网络部分失效的情况下，有些节点和边会出现阻塞或故障，为完成器材物资的保障任务，在运的物资将在某些路段采取迂回的形式继续，从而导致网络的物资输送效率有所降低。当网络中的很多节点和边出现阻塞或故障时，保障网络将被分割成若干子网络，破坏节点间的连通性，造成没有可行的迂回路径。具有良好抗毁性的保障网络，在某个节点或边出现故障或者阻塞时，其网络的运输效率变化值应当控制在一个可接受的范围内;否则，保障网络的抗毁性能力低下。为此，定义网络效率来衡量网络应对这种由于高负载或网络部分失效带来的运行效率变低的能力。

定义整个网络的效率(ηE)为网络中任意2个节点之间最短距离倒数之和的平均值，即

2．3 保障业务层抗毁性测度

2．3．1 器材到达率

装备器材保障网络的根本目的是满足装备维修的器材需求，因此，器材到达率是衡量装备保障网络业务抗毁性的重要指标。

定义第i个需求点的器材到达率ψi为实际到货量与需求量的比值，即

式中:dij为节点i与j之间的最短距离。

网络效率反映了网络的连通能力，能够表征全局网络的拓扑结构抗毁性。当网络的连通能力越好、越高时，则ηE越大。令ηE0为网络在正常情况下的效率，则突发事件后网络的效率与正常情况下的效率之比(ξ)能够反映突发事件对网络运行的影响程度，即

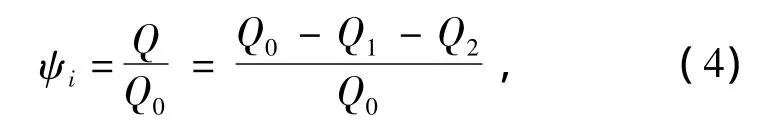
式中:Q为器材的实际到货量;Q0为器材的器材的原始需求量。

某时刻网络发生部分节点中断，导致部分器材流受到影响。这部分受影响的器材流分为2类:1)器材流可以通过路径迂回继续完成保障任务，虽然最终能到达需求点，但供应时间可能会超出最大等待时间，对于超出时间限制的这部分器材流，本文认为也是没有满足需求点的器材需求，用Q1表示，而对于通过路径迂回在保障时间范围内到达需求点的这部分器材，则认为其满足需求点的器材需求;2)器材流所在路径两端的节点都被中断了，这部分器材流被孤立，考虑到用户最大等待时间限制，认为这部分器材流在最大等待时间内无法完成保障任务，用Q2表示。在计算器材到达率时，假设网络中各保障点的器材库存量充足，能够从品种、数量上满足需求点的器材需求。

可见:ψi越大，表明网络的抗毁性能力越高，ψi越小，则网络的抗毁性能力越低;器材到达率实质上是对突发情况下器材损失程度的衡量指标。

定义整个网络的器材到达率ψ为各需求点器材到达率的平均值，即

2．3．2 用户等待时间

由于保障网络的军事特性，网络中的需求点对器材到货时间有一定的要求，特别是在应急情况下，用户等待器材的时间应当控制在一定的范围内。为此，有必要从保障时间角度研究相应的业务抗毁性测度指标。因此，将用户等待时间作为衡量指标。

定义需求点i的用户等待时间TWi为点i从发出需求时刻Tstart到收到全部器材时刻Tend的时间间隔，即

当网络发生服务中断，原始需求不能全部被满足时，Tend代表最大等待时间。

定义整个网络的平均用户等待时间TW为所有需求点的用户等待时间的平均值，即

由各抗毁性指标计算公式的构成可以看出:在拓扑结构抗毁性指标中，对于给定的网络，网络鲁棒性计算较为简单，而网络效率只与网络中的最短路径相关。最短路径计算可由Dijkstra方法得出［11］。保障业务抗毁性测度指标的计算则相对复杂，需要设计专门的算法，具体算法参见文献［12］。

3 装备器材保障网络抗毁性仿真实验

3．1 网络拓扑层抗毁性仿真

3．1．1 网络鲁棒性仿真

图4为网络在随机攻击和蓄意攻击下的网络鲁棒性变化曲线，x轴为被攻击的节点数量n攻占节点总数量n总的百分比(n攻/n总)，表示攻击强度;y轴为网络鲁棒性值，图中的每个数据点都是取10次模拟攻击后计算的鲁棒性平均值。

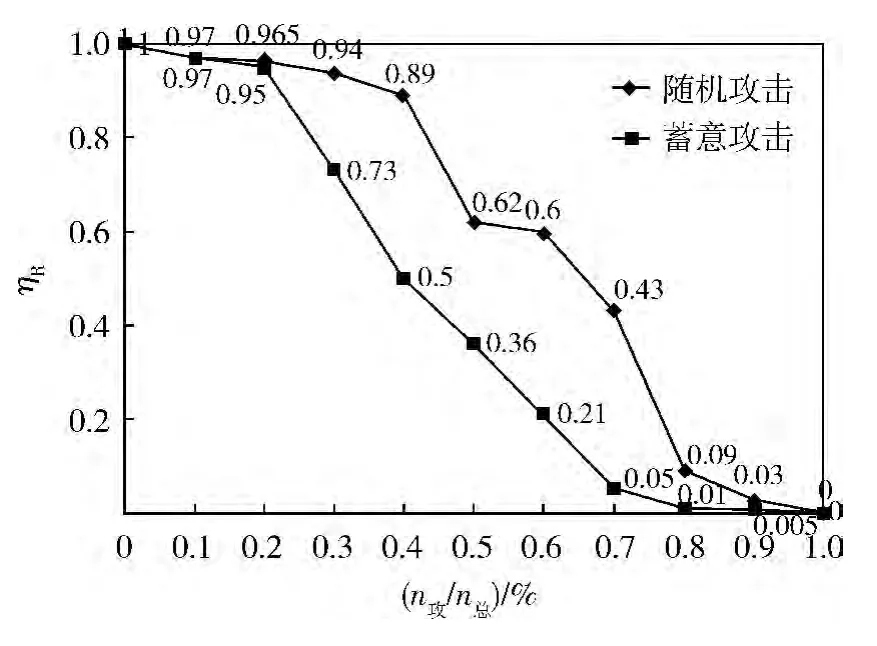
图4 网络鲁棒性变化曲线

由图4可知:2种攻击模式下的网络鲁棒性均随攻击强度的增大而减小;且蓄意攻击下网络鲁棒性减小得更快，表明蓄意攻击对网络鲁棒性的影响比随机攻击大。当攻击强度小于0．2时，网络鲁棒性都能保持在0．95以上，表明本文所构建的网络在面对小规模打击失效时具有较强的抗毁性;而攻击强度一旦超过0．2，2种攻击都能使网络的鲁棒性急剧下降:因此，称点0．2为网络鲁棒性的“下降临界点”。在随机攻击下，当攻击强度达到0．9时，网络几乎陷入瘫痪;在蓄意攻击下，当攻击强度达到0．8时，网络瘫痪:表明蓄意攻击比随机攻击更能使网络快速陷入瘫痪，且称点0．8为网络鲁棒性的“瘫痪临界点”。究其原因，在蓄意攻击下，每次攻击的都是网络中最为重要的节点，导致网络快速陷入瘫痪。因此，在安排防御资源时，应当加强对重要节点的防御。

3．1．2 网络效率仿真

图5为网络在随机攻击和蓄意攻击下网络效率随攻击强度的变化曲线，图中的每个数据点都是取10次模拟攻击后计算的网络效率平均值。

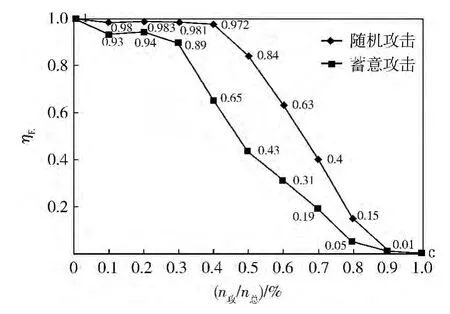
图5 网络效率随攻击强度变化曲线

由图5可知:随着攻击强度的增大，2种攻击模式下的网络效率均呈下降趋势;且蓄意攻击下网络效率下降速度比随机攻击下的下降速度更快，表明蓄意攻击对网络效率的影响更大。随机攻击下的下降临界点出现在攻击强度为0．4时，也就是说当网络中40%的节点遭到随机攻击时，拓扑层抗毁性能开始大幅度下降，对比王文峰［13］的研究结论(网络中大概25%的节点遭到攻击时，网络连通性能开始出现大幅度下降)，本文所构建的装备器材保障网络拓扑层具有较好的抗毁性能。蓄意攻击下的下降临界点出现在攻击强度为0．3时，比随机攻击下的下降临界点略小。2种攻击模式下的瘫痪临界点都出现在攻击强度为0．9。在随机攻击下，下降临界点出现之前，网络效率几乎不受外界中断的影响，当攻击强度达到0．5时，网络效率仍然能够维持在0．8以上，表明:本文所构建的网络对随机攻击表现出较好的抗毁性;而对蓄意攻击，网络的抗毁性则相对较弱。

3．2 保障业务层抗毁性仿真

3．2．1 器材到达率仿真

图6为网络在随机攻击和蓄意攻击下器材到达率随攻击强度的变化曲线，图中的每个数据点都是取10次模拟攻击后计算的器材到达率平均值。

由图6可知:2种攻击模式下的器材到达率在整体上均随攻击强度的增大而减小;且蓄意攻击下器材到达率的下降速度更快，表明蓄意攻击对器材保障的影响更大。蓄意攻击下的下降临界点出现在攻击强度为0．2时，而随机攻击下的下降临界点在攻击强度为0．5时才出现，表明网络对随机攻击表现出较好的抗毁性。蓄意攻击下的瘫痪临界点在攻击强度为0．6时就出现了，表明网络业务层很容易受外界因素影响，因此，在实际保障中，必须建立相应的优化和应急预案，保证器材保障任务的顺利完成。

图6 器材到达率随攻击强度变化曲线

3．2．2 用户等待时间仿真

图7为网络在随机攻击和蓄意攻击下用户等待时间随攻击强度的变化曲线，图中的每个数据点都是取10次模拟攻击后计算的用户等待时间平均值。实验中，取平均用户最大等待时间为120 min。另外，在网络节点被全部中断(攻击强度为1)时，网络处于完全瘫痪状态，此时的用户等待时间理论上应为无穷大，考虑到程序实现的可行性，取1 000 min作为无穷大值。

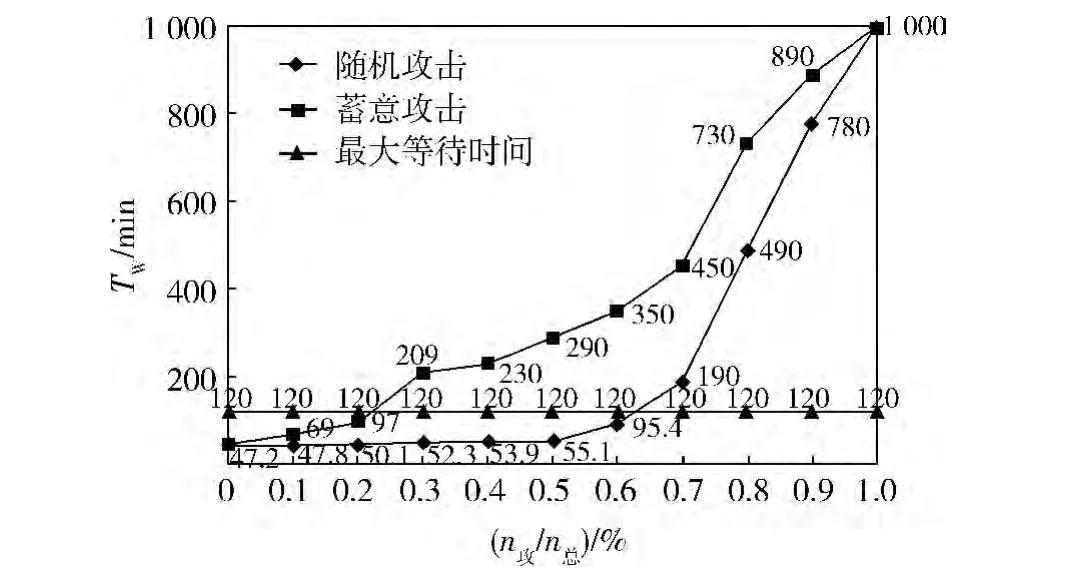
图7 用户等待时间随攻击强度变化曲线

由图7可知:2种攻击模式下的用户等待时间在整体上均随攻击强度的增大而增大，这是因为网络节点的中断数量直接影响保障路径的选择和保障车辆的行驶时间。在随机攻击下，攻击强度达到0．7时，用户等待时间才超过用户最大等待时间;在蓄意攻击下，攻击强度为0．3时，用户等待时间就已超过用户最大等待时间:2个攻击强度值相差较大，表明外界中断对网络的用户等待时间(或用户满意度)有较大影响。在随机攻击下，用户等待时间在攻击强度为0．5之前几乎没有多大变化，表明网络对随机攻击具有很好的抗毁性能，之所以出现这种情况，是因为随机攻击具有“盲目性”，虽然有众多节点遭到攻击，但是没有对过多保障车辆的行驶路线造成太大影响。

4 结论

本文对装备器材保障网络计算机仿真模型及网络的抗毁性测度方法进行了研究。通过网络抗毁性仿真实验，验证了本文所构建的装备器材保障网络具有较强的拓扑层抗毁性。但保障业务层的抗毁性较弱，下一步，将对提高装备器材保障网络业务层抗毁性的策略、措施展开深入研究，以进一步提高装备保障网络在应急条件下的生存能力。

［1］ 王宗喜，徐东．军事物流学［M］．北京:清华大学出版社，2007．

［2］ Lawrence V S，Mark S D．Reliability Models for Facility Location:the Expected Failure Cost Case［J］．Transportation Science，2005，39(3):400-416．

［3］ Daskin M S，Stern E H．A Hierarchical Objective Set Covering Model for Emergency Medical Service Vehicle Deployment［J］．Transportation Science，1981，15(2):137-152．

［4］ 温巧林，司守奎，孙玺菁，等．军事通信网络抗毁性指标函数研究［J］．信息系统工程，2010(6):48-49．

［5］ 刘啸林．网络抗毁性研究及其在证券交易网络中的应用［D］．上海:华东师范大学，2007．

［6］ Brostrom P，Holmberg K．Multi Objective Design of Survivable IP Networks［J］．Annals of Operations Research，2006，147(1):235-253．

［7］ 王伟．铁路网抗毁性分析与研究［D］．北京:北京交通大学，2011．

［8］ 谈革新．复杂网络拓扑层抗毁性测度研究［D］．南京:南京理工大学，2011．

［9］ Ghashghai E，Rardin R L．Using a Hybrid of Exact and Genetic Algorithms to Design Survivable Networks［J］．Computers＆ Operations Research，2002，29(1):53-56．

［10］ Ellison R J，Linger R C，Longstaff T，et al．R Survivable Network System Analysis:a Case Study［J］．IEEE Software，1999，16(4):70-77．

［11］ 胡运权，郭耀煌．运筹学教程［M］．北京:清华大学出版社，2003．

［12］ 梁波．基于抗毁性的装备器材保障网络设计与优化方法研究［D］．北京:装甲兵工程学院，2012．

［13］ 王文峰．装备保障网络优化设计问题研究［D］．长沙:国防科学技术大学，2008．