参数对2A12铝合金微动疲劳局部塑性影响分析

陈跃良,徐丽,2,张勇,郁大照

(1.海军航空工程学院青岛校区,山东青岛266041; 2.海军航空兵学院,辽宁葫芦岛125001)

理论与实验研究

参数对2A12铝合金微动疲劳局部塑性影响分析

陈跃良1,徐丽1,2,张勇1,郁大照1

(1.海军航空工程学院青岛校区,山东青岛266041; 2.海军航空兵学院,辽宁葫芦岛125001)

目的研究局部塑性对微动疲劳的影响。方法建立2A12铝合金圆柱/平面微动疲劳有限元模型,考虑塑性作用进行有限元分析,研究微动疲劳参数对局部塑性的影响。结果局部塑性变形发生在试件表面或次表面,最大等效塑性变形随着微动垫半径的减小而增大。随着轴向应力的增加,最大切向应力增加;随着摩擦系数的增加,剪应力的最大值急剧增加,粘着区增加,滑移区减小,但摩擦系数对整个接触区的大小没有影响。结论微动疲劳参数对局部塑性有一定的影响。

2A12铝合金;有限元;微动疲劳参数;局部塑性

微动疲劳接触分析是寿命预测的基础,在国外,早期许多研究者采用解析法研究微动接触应力场,但解析解只适应于理想情况下的应力分析,否则只能采用数值法[1—2],如边界元法、有限元法等。Harish Ganapathy[3—4]建立了蒙皮/铆钉微动接触有限元分析模型,计算了应力分布并预测裂纹萌生位置及寿命。赵华、周仲荣等[5—6]建立圆柱/平面接触有限元分析模型,分析了切向和径向微动接触区内的应力分布,提出了虚拟接触载荷法。刘军等[7]应用ANSYS有限元软件建立方足微动桥/试样接触有限元模型,分析了不同条件下接触面上的应力分布,发现接触表面拉应力和剪应力在粘滑交界处存在突变,认为这一区域是裂纹萌生区,试验结果与计算结果吻合较好。周文等[8]建立圆柱/平面接触有限元模型,分析了摩擦系数对Von Mises应力、最大接触压力和表面拉应力的影响。结果表明,摩擦系数越大,越易产生裂纹。

根据微动疲劳试验分析发现,尽管微动疲劳接触机制总体上是弹性的,但也会有局部塑性区,塑性变形是微动疲劳中的组成部分。塑性变形产生的残余应力场会改变接触面附近的应力应变范围而影响裂纹成核。人们对微动接触有限元分析很多,但大多只考虑应力应变的弹性变化,考虑塑性影响分析的很少,且大多只见于国外的一些文献资料[9—13]。文中利用ABAQUS有限元进行建模,考虑塑性作用对圆柱/平面微动疲劳接触进行有限元分析,研究了参数变化对局部塑性的影响。

1 有限元模型

对于2A12铝合金材料,热处理方式为:加热到(494±5)℃,保温数小时,然后放入水中冷却96 h,检查硬度和抗拉强度是否符合规定的要求,抗拉强度σb≥392.5 MPa。其屈服强度、弹性模量和泊松比分别为:σy=342 MPa,E=69 GPa,v=0.33。根据对称性,用ABAQUS有限元软件对整个结构(如图1所示)的一半进行建模,分析模型试件的宽度和高度分别为20 mm和1.75 mm,微动垫的宽度和高度分别为10 mm和12 mm。试件底端在y方向的位移为0,微动垫左端和右端在x方向的位移都为0,另外为了保证微动垫顶端各节点的位移相同,在该面上施加了多点约束(MPC)。

图1 微动疲劳试验示意Fig.1 Schematic of a fretting fatigue test

在该研究中,对微动疲劳接触模拟模型进行改进,所建模型为二维模型,采用四节点(双线性)平面应力四边形非协调单元(CPS4I)。试件和微动垫接触定义为主-从接触,微动垫下端底面为接触主面,试件上表面为接触从面。载荷分3步施加,第1步首先施加接触载荷P,使微动垫与试件之间建立接触关系;第2步分别在试件右端和试件左端施加最大轴向应力σ和响应应力σr,与试验中施加最大循环载荷状态一致;第3步分别在试件右端和试件左端施加最小轴向应力σ和响应应力σr,与试验中施加最小循环载荷状态一致。响应应力可以通过式(1)、式(2)计算:

式中:F为施加于试件下端的轴向力;Fr为试件上端的响应轴向力,通过测力传感器测得;Q为切向力;As为分析模型试件横截面积。有限元模型如图2所示,在改进的有限元模型中,施加的轴向应力和响应应力值的差使试件产生微动。

图2 微动疲劳有限元分析模型Fig.2 Finite element analysis model for fretting fatigue

在微动疲劳接触模型有限元分析中,可以考虑的一些塑性模型有:弹性/完全塑性、各向同性应变、动态应变硬化。研究表明[14],材料塑性变形量不受塑性模型选取的影响,但是与其他塑性模型相比,应用动态应变硬化模型,塑性应变区中的棘轮面积明显降低。此外,循环塑性应变对循环载荷和应变硬化不敏感,而棘轮效应则对循环载荷和应变硬化非常敏感。文献[15]通过对7075铝合金和2024铝合金的微动疲劳研究表明,这些特性对应变速率并不敏感,因此它们用各向同性硬化弹塑性模型来模拟微动疲劳。文中用双线性弹塑性本构方程来体现2A12铝合金微动疲劳接触弹塑性响应进行分析。

2 微动疲劳参数影响

影响材料微动疲劳的因素有很多,可分为主要变量和次要变量。下面研究几个主要变量对接触面局部塑性的影响。

2.1 微动垫半径的影响

在有限元分析中,摩擦系数f是输入变量,随着接触表面的不同会发生变化。Szolwinski[16]等通过对2024铝合金微动疲劳的研究表明,产生微动时的摩擦系数为0.65,文中选f=0.5作为输入变量来研究不同的微动垫半径对局部塑性的影响。其他参数:微动垫半径r为115,180 mm,接触压力P=450 N,轴向应力σ为180,220,308,331 MPa。

切向应力随微动垫半径的变化规律如图3所示,横坐标表示粘着区与接触半宽的比值。可以看出,在所有情况下,切向应力最大值(σxx)max都位于微动接触界面的后缘,并且在所有轴向载荷作用下,切向应力最大值随着微动垫半径的减小而增加。此外,当轴向应力为308和331 MPa时,对于所有微动垫半径,其最大切向应力都超过屈服应力,而对于轴向应力为180和220 MPa时,只有微动垫半径为115 mm时,其最大切向应力才超过屈服应力。

P=450 N,σ=331 MPa,r=115 mm条件下等效塑性应变如图4所示,可以看出,最大塑性变形在接触界面的后缘形成,即裂纹成核位置,并成约45°方向扩展,这与试验观察非常一致。

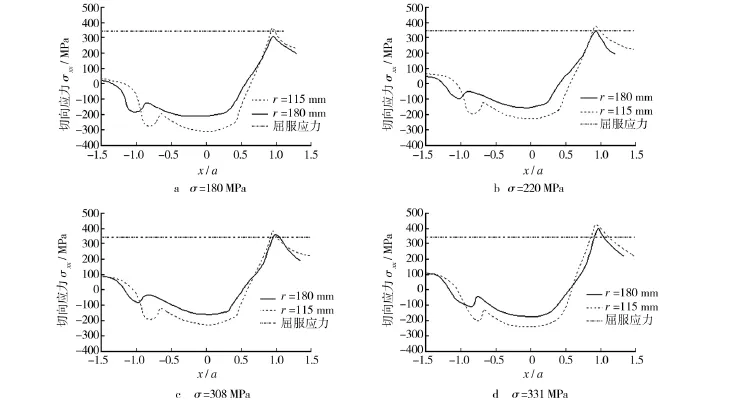
图3 切向应力分布Fig.3 Tangential stress distribution

图4 等效塑性应变(σ=331 MPa)Fig.4 Equivalent plastic strain contour plot(σ=331 MPa)

2.2 轴向应力的影响

为了研究轴向应力对接触面局部塑性的影响,假定P=900 N,r=180 mm,f=0.5,计算轴向应力分别为180,220,308,331 MPa时接触面的局部塑性。

最大主应变沿接触界面的变化如图5所示,可以看出,沿接触界面最大主应变的峰值随轴向应力的增大而增加,并且这些峰值都出现在接触界面的后缘或靠近接触界面后缘。

图5 接触面最大主应变分布Fig.5 Maximum principal strain distribution at the contact interface

图6 等效塑性应变(σ=180 MPa)Fig.6 Equivalent plastic strain contour plot(σ=180 MPa)

轴向应力为180 MPa时的等效塑性应变如图6所示,可以看出,裂纹可能成核于接触区下面的试件内部,主要是由于微动使试件产生微裂纹,在轴向应力作用下裂尖处产生应力集中,即在接触面下方几微米处的试件内部应力高于接触界面的微动应力。由此可以得出:微裂纹成核于试件的表面或离表面非常近的试件内部,这也与试验观察非常一致。

2.3 摩擦系数的影响

为了研究摩擦系数对接触面局部塑性的影响,假定P=450 N,r=180 mm,σ=331 MPa,计算摩擦系数从0.3到1.1时接触面的局部塑性。

接触面剪应力分布随摩擦系数的变化规律如图7所示,可以看出,随着摩擦系数的增加,剪应力的最大值急剧增加,粘着区增加,滑移区减小,这说明摩擦系数的增加增强了微动垫与试件之间的粘着力。同时在其他参数不变的情况下,摩擦系数分别对粘着区和滑移区都有较大的影响,但对整个接触区的大小没有影响。

图7 不同摩擦系数下接触面剪应力分布Fig.7 Shear stress distribution at contact surface with different coefficients of friction

3 结论

1)Von Mises应力峰值和最大塑性变形都位于接触界面的后缘或靠近接触界面后缘的位置,通常微动接触应力会急剧减少,产生较陡的应力梯度。Von Mises应力峰值和最大塑性变形也会位于接触后缘试件内部,即局部塑性发生在试件表面或次表面,也即裂纹成核于试件表面或次表面。

2)最大等效塑性变形随着微动垫半径的减小而增大,对于所有微动垫半径,最大塑性变形出现在接触面的后缘,而当微动垫半径减小时,最大塑性变形可能会出现在接触界面处试件内部。

3)随着轴向应力的增加,最大切向应力(σxx)max增加。对于所有轴向应力水平,最大等效应力和最大塑性变形位置都在接触界面的后缘或靠近接触界面后缘。

4)随着摩擦系数的增加,剪应力的最大值急剧增加,粘着区增加,滑移区减少。摩擦系数对粘着区和滑移区都有较大的影响,但对整个接触区的大小没有影响。

[1] KIMURA T,SATO K.SimPlified Method to Determine Contact Distribution and Tress Intensity Factors in Fretting Fatigue[J].International Journal of Fatigue,2003 (1):1—7.

[2] NABOULSI S,MALL S.Fretting Fatigue Crack Initiation Behavior Using Process Volume Approach and Finite Element Analysis[J].Tribology International,2003,36: 121—131.

[3] HARISH G,FARRIS T N.Modeling of Skin/Rivet Contact:Application to Fretting Fatigue[R].AIAA-97-1340,1997.

[4] HARISH G,FARRIS T N.Effect of Fretting Contact Stresses on Crack Nucleation in Riveted Lapjoints[R].AIAA-98-1746,1998.

[5] 赵华,周仲荣.数值方法在微动疲劳研究中的应用进展[J].摩擦学学报,2000,20(4):317—320. ZHAO Hua,ZHOU Zhong-rong.The Application Progress of Numerical Method on Fretting Fatigue[J].Tribology, 2000,20(4):317—320.

[6] 赵华,金雪岩,朱民昊.微动接触应力的数值分析[J].四川大学学报,2003,35(5):32—36. ZHAO Hua,JIN Xue-yan,ZHU Ming-hao.Numerical A-nalysis of Fretting Contact Stresses[J].Journal of Sichuan University,2003,35(5):32—36.

[7] 刘军,刘道新,刘元镛.微动接触应力的有限元分析[J].机械强度,2005,27(4):504—509. LIU Jun,LIU Dao-xin,LIU Yuan-yong.Finite Element A-nalysis for Fretting Contacting Stresses[J].Journal of Mechanical Strength,2005,27(4):504—509.

[8] 周文,孙伟明,屠立群.微动摩擦力的有限元分析[J].甘肃科技,2007,23(6):93—95. ZHOU Wen,SUN Wei-ming,TU Li-qun.Finite Element Analysis for Fretting Frictional Force[J].Gansu Science and Technology,2007,23(6):93—95.

[9] AMBRICO J M,BEGLEY M R.Plasticity in Fretting Contact[J].Mech Phys Solids,2000,48(11):2391—2417.

[10]AMBRICO J M,BEGLEY M R.The Role of Macroscopic Plastic Deformation in Fretting Fatigue Life Predictions [J].International Journal of Fatigue,2001,23:121—128.

[11]GOH C-H,MCDOWELL D L.Plasticity in Polycrystalline Fretting Fatigue Contacts[J].Journal of the Mechanics and Physics of Solids,2006,54:340—367.

[12]杨茂胜,毕玉泉.微动接触应力影响因素研究[J].装备环境工程,2012,9(1):5—22. YANG Mao-sheng,BI Yu-quan.Study on Influencing Factors for Fretting Contacting Stresses[J].Equipment Environmental Engineering,2012,9(1):5—22.

[13]徐丽,陈跃良,衣林,等.铝合金微动疲劳研究及展望[J].强度与环境,2011,8(4):63—72. XU Li,CHEN Yue-liang,YI Lin,et al.Study of Aluminum Alloy Fretting Fatigue[J].Equipment Environmental Engineering,2011,8(4):63—72.

[14]AMBRICO J M,BEGLEY M R.The Role of Macroscopic Plastic Deformation in Fretting Fatigue Life Predictions [J].International Journal of Fatigue,2001(5):121—128.

[15]KINDERVATER C M,JOHNSON A,KOHLGRIIBER D, et al.Crash and High Velocity Impact Simulation Methodologies for Aircraft Structures[J].Structural Failure and Plasticity,2000,345—352.

[16]SZOLWINSKI M P,FARRIS T N.Mechanics of Fretting Fatigue Crack Formation[J].Wear,1996,198:93—107.

Analysis of Impact of Parameters on the Localized Plasticity of 2A12 Aluminum Alloy Fretting Fatigue

CHEN Yue-liang1,XU Li1,2,ZHANG Yong1,YU Da-zhao1

(1.Qingdao Branch of Naval Aeronautical Engineering University,Qingdao 266041,China; 2.Institute of Naval Aviation,Huludao 125001,China)

Objective To study the effects of localized plasticity on fretting fatigue.Methods The 2A12 aluminum alloy cylindrical/plane fretting fatigue FEA model was established,FEA analysis was performed considering the plasticity,and the effect of fretting fatigue parameters on localized plasticity were studied.Results The results indicated that the localized plasticity occurred on the surface or sub-surface of the sample,and the maximum equivalent plastic deformation increased with decreasing fretting pad radius.With increasing axial stress,the maximum tangential stress increased.With increasing COF,the maximum value of shear stress increased sharply,the stick zone increased and the slip zone decreased,however,COF had no effect on the size of the whole region.Conclusion The parameters of fretting fatigue had certain effects on localized plasticity.

2A12 aluminum alloy;FEM;fretting fatigue parameters;localized plasticity

10.7643/issn.1672-9242.2014.05.001

TG146.2+1

:A

1672-9242(2014)05-0001-05

2014-05-14;

2014-06-07

Received:2014-05-14;Revised:2014-06-07

国家自然科学基金资助项目(51075394,51375490)

Fund:Supported by the National Natural Science Foundation of China(51075394,51375490)

陈跃良(1962—),男,浙江人,教授,博士生导师,主要研究方向为复杂环境下飞机结构寿命评定、结构疲劳与可靠性。

Biography:CHEN Yue-liang(1962—),Male,from Zhejiang,Professor,Research focus:lifetime evaluation,fatigue and reliability of aircraft structures in complex environments.