基于单神经元自适应PSD的汽包液位控制

常杰锋，陈 圆

（中冶南方工程技术有限公司 自动化设计二所，武汉 430223）

在工业控制领域，锅炉汽包液位的控制是锅炉运行的重要环节，稳定的汽包液位是保证锅炉运行安全、提高锅炉运行效率的重要因素。锅炉运行过程中，汽包液位同时受锅炉负荷变化、工作环境等多种因素的影响，其动态特性具有惯性大、滞后时间长、非线性时变的特点，因此汽包液位的稳定控制问题比较复杂。实际中应用较多的三冲量PID控制方法统筹考虑了锅炉负荷、给水流量波动对汽包水位造成的影响，在锅炉汽包稳定工况下控制品质良好。该控制方法的PID参数在运行初期通过人工整定获得，这在实际工程中往往难以一次性整定得到最佳状态，并且随着锅炉运行时间、工况的变化，PID参数可能需要不定期的人工重新整定，这不利于锅炉连续安全运行。

神经网络是工业控制领域中具有重要影响的先进控制方法，它模拟人的思维活动，是解决非线性和不确定性系统的有效工具。当前，将神经网络与PID控制相结合是一个新的研究热点。其中，单神经元自适应PSD算法是数字PID算法与神经网络的有效结合，其物理意义明确、易于工程实现。

本文针对汽包液位控制中存在的问题，提出基于单神经元自适应PSD算法的液位控制方法，在保留了传统三冲量控制方法优点的同时，获得神经网络的自学习、自适应和非线性处理能力，提高了控制品质。

1 锅炉汽包工艺流程

锅炉汽包工艺流程如图1所示，水在泵的输送力作用下流向汽包，流动过程中受炉膛的加热不断升温直至汽化，到达汽包后水和蒸汽分离。水汇集于汽包下部，通过下降管和上升管受热持续自循环汽化。蒸汽在汽包上部聚集并向外输送，用来驱动汽轮机等设备。汽包给水流量大小通过泵出口调节阀开度变化或者泵转速变化来调节。

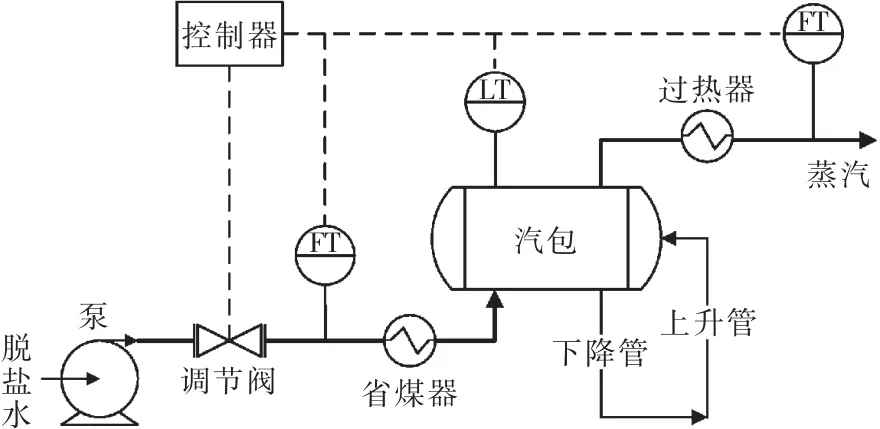
图1 锅炉汽水工艺流程示意图Fig.1 Flow of boiler

在锅炉运行过程中，汽包液位稳定的影响因素有很多，其中主要的是给水流量和蒸汽流量。当给水流量增加时，由于给水的温度相对较低，从原有饱和水中吸收热量，对汽包水容积有减小作用，所以汽包水位刚开始不会立即上升，而是表现出起始惯性段；当蒸汽负荷增加时，从物料平衡方面讲，蒸汽量大于给水量，水位应该下降，但是实际中，蒸汽负荷突然增加会造成汽包压力降低，汽水混合物中蒸汽容积迅速增加，水位反而迅速上升，即“虚假水位”现象[1]。另外，随着锅炉设备运行时间的增加以及环境因素变化，炉体内影响汽水变化的对流管束的物理特性会随之发生变化，这会引起模型失配的问题。总之，锅炉汽包液位系统是一个惯性大、滞后时间长、非线性时变的系统。

2 汽包液位控制方法

2.1 整体框架结构

鉴于锅炉运行过程中，汽包液位控制的复杂性，本文采用基于单神经元自适应PSD算法的锅炉汽包液位控制方法。如图2所示，该方法借鉴传统的三冲量PID控制的优点，同样以汽包液位、给水流量和蒸汽流量三个变量作为处理对象，控制系统整体采用前馈+串级的结构。其主调节器采用以汽包液位为检测和控制变量的常规PID调节器，汽包液位的设定值与实际测量值的偏差经过PID调节器运算的输出为给水流量的设定值；汽包外供蒸汽流量测量值作为前馈量，来抑制“虚假液位”对汽包液位稳定的不利影响。

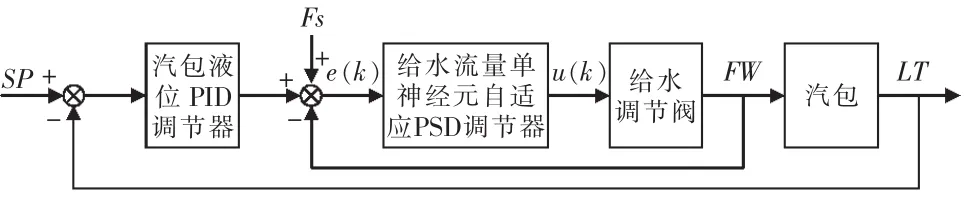
图2 基于单神经元自适应PSD算法的锅炉汽包液位控制框图Fig.2 Boiler drum level control based on single neuron adaptive PSD algorithm

图2 中，LT为汽包液位实际测量值；Fw为给水流量实际测量值；Fs为蒸汽流量实际测量值；SP为汽包液位设定值；e（k）为给水流量偏差值；u（k）为给水流量调节器输出值，作为给水调节阀的开度给定值。

其副调节器采用以给水流量为检测和控制变量的单神经元自适应PSD调节器，这优于传统的三冲量PID控制。副调节器处于控制框图的内环，主调节器和前馈量的作用整合后最终通过副调节器作用给执行机构（如调节阀、变频泵等），因此一方面“虚假液位”等因素带来的波动在副调节器输入前已抵消，使副调节器的运算更加平稳快捷；另一方面，副调节器所具备的自适应等优秀特性可使控制全局获得。

2.2 单神经元自适应PSD调节器设计

作为副调节器的单神经元自适应PSD调节器结合数字PID、神经网络和自适应算法的特点，利用三输入单神经元节点模拟常规PID，同时进行三个参数的动态优化和增益的在线自学习调整。该算法无需辩识过程参数，只要在线检测出期望输出和实际输出，即形成自适应控制规律。

2.2.1 控制原理

单神经元自适应PSD调节器的控制原理如图3所示，包括三部分的功能：输入转换、神经推理、参数自学习。

图3 单神经元自适应PSD控制框图Fig.3 Single neuron adaptive PSD control diagram

（1）输入转换

将主调节器输出的给水流量设定值、前馈量（汽包外供蒸汽流量测量值Fs）与给水流量实际测量值 Fw 取差值，得到给水流量偏差值 e（k），e（k）即单神经元自适应PSD调节器的输入值。e（k）通过算法转换器转换得单神经元的三个输入分别为：x1（k）=Δe（k），x2（k）=e（k），x3（k）=Δ2e（k）。 转换方程见式（1）。三个输入分别对应对给水流量偏差值e（k）的比例、积分、微分作用。

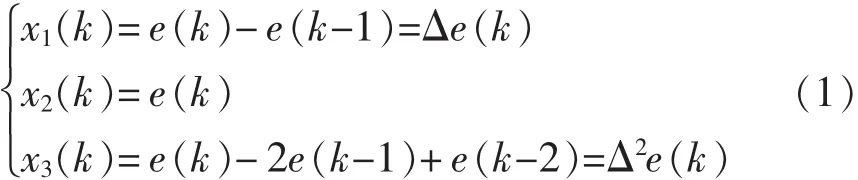
（2）神经推理

单神经元三个输入 x1（k）、x2（k）、x3（k）通过单神经元的推理运算得到给水调节阀的阀位变化值Δu（k），Δu（k）与原输出给定阀位值 u（k-1）求和得调节器输出u（k）作为给水调节阀的开度给定值。单神经元自适应PSD控制的推理运行方程为

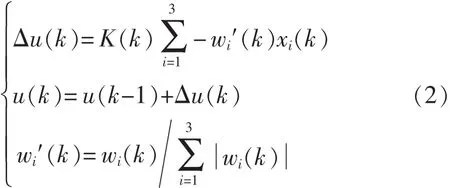
式中：K（k）为全局增益系数；wi′（k）为归一化的输入权系数。

（3）参数自学习

给水流量调节器输出后，根据实际的汽包液位控制效果，对比汽包液位测量值、蒸汽流量测量值、给水流量测量值和其相应的设定值，取相应偏差值 e（k）、调节器输出值 u（k），进行算法参数—权系数和全局增益的自学习、自适应，来优化控制参数。

权系数 wi（k）的自学习：连接权系数 wi（k）的学习策略采用有监督Hebb学习规则，规则表达式如式（3）所示，神经元根据给水流量偏差值 e（k）的变化对环境信息进行相关学习和自组织，使相应的输出增强或削弱。

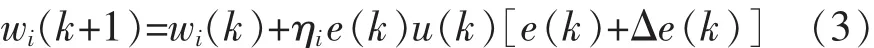
式中，ηi∈［0，1］为学习速率。

全局增益K的自学习：全局增益系数K（k）根据给水流量偏差值e（k）的变化采用由Marsik给出的递推算式在线学习方法[2]：

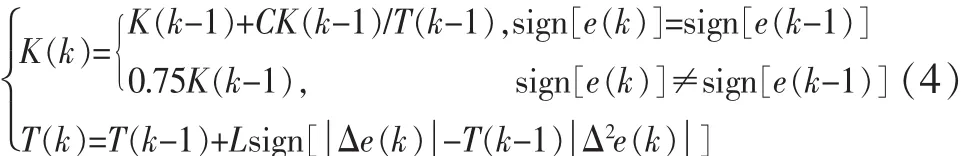
式中： 学习系数 C∈［0.025，0.05］；L∈［0.05，0.1］；sign（x）为符号函数。

2.2.2 程序实现

在锅炉汽包液位控制系统的程序编程中，根据神经元自适应PSD控制原理式（1）～式（4），实现给水流量调节，控制流程如图4所示。

图4 单神经元自适应PSD控制程序流程图Fig.4 PSD control program flow of single neuron adaptive

第 1 步 确定算法常数 ηi、C、L 的取值。 η1、η2、η3表征比例作用、积分作用、微分作用的学习强度，其取值调整方法类似于PID系数。若系统上升时间太长，可增大η1、η3；若超调迅速下降至低于给定值，此后，又缓慢上升至稳态，时间太长，则可减少η1，增加积分项作用 η2；系统延时大，为减少超调，η1、η3应该适当大些。根据神经元网络的特点，其初值可设定为 η1=η2=η3=0.02。 学习常数 C、L 过大，全局增益系数K变化太快，调节器易超调；C、L过小，全局增益系数K变化太慢，神经元调节器调节优化过程缓慢。

第2步 确定神经元连接权系数初始值wi（0）、增益K的初始值K（0）、Marsik递推算式T的初值T（0）。增益K的取值，若系统超调过大，则减小，若过渡过程时间太长，则增大。权系数初始值wi（0）和增益K的初始值K（0）按照下式确定[3]：

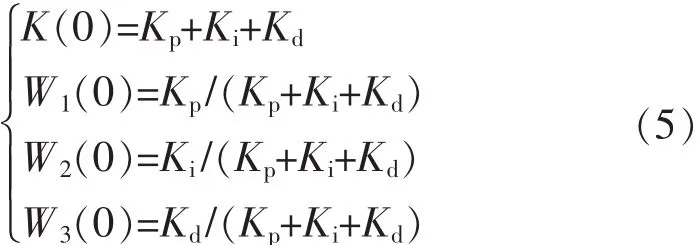
式中：Kp，Ki，Kd为 PID 控制器的最优整定值。传统三冲量PID控制器中脱开主调节器回路和前馈量的作用，使用试凑法或者飞升曲线法对副调节回路的PID控制器进行整定，获得Kp，Ki，Kd的最优整定值。由于神经元的自学习能力，权系数的初值对权系数以后的学习效果影响不大，一般可以选择0.01～1.00之间的3个相等的数。 通常取 T（0）=L。

第3步 从工艺系统仪表测量获得汽包液位、给水流量以及蒸汽流量的实际值。

第4步 计算给水流量偏差信号e（k），并根据算法公式得到单神经元输入xi（k）。

第5步 控制器计算给水调节阀阀位输出给定值 u（k）。

第6步 根据算法公式修正算法参数—权值wi（k）、K（k）、T（k）。

第7步 k=k+1，返回第3步。

3 实际应用

在某厂75 t/h燃气锅炉汽包液位控制系统中，按照本文所述基于单神经元自适应PSD算法的控制方法对其原三冲量PID控制进行改进。系统原控制算法的副调节回路的PID参数在运行初期70 t/h负荷下整定得Kp=8、Ki=1、Kd=0，获取锅炉运行在60 t/h负荷、70 t/h负荷下的汽包液位趋势如图5（a）、5（c）。 切换至改进算法后，取初值 K（0）=9、w1（0）=0.9、w2（0）=0.1、w3（0）=0、η1=η2=η3=0.02、C=0.025、T（0）=L=0.05。经过算法自学习，参数逐步收敛，获取锅炉运行在60 t/h负荷下的汽包液位趋势如图5（b），此时单神经元自适应PSD控制算法参数K=7.56、w1=0.88、w2=0.14、w3=0.05； 获取锅炉运行在70 t/h负荷下的汽包液位趋势如图5（d），此时单神经元自适应PSD控制算法参数K=8.72、w1=0.92、w2=0.11、w3=0.04。

通过对比图 5 中（a）～（d）的趋势曲线发现，算法改进后的液位控制系统可自学习适应不同负荷状态下，锅炉运行进入稳定状态后，汽包液位（液位设定值SP=0 mm）在0 mm上下的波动幅度减小，波动频率降低，相对算法改进前更加稳定。

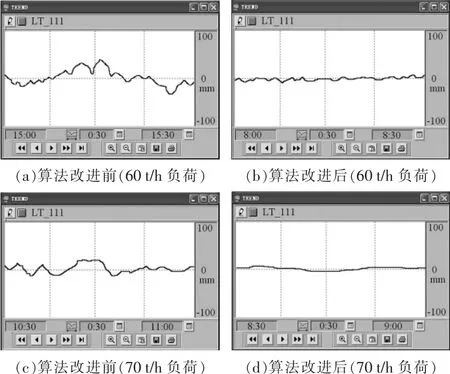
图5 汽包液位趋势图Fig.5 Boiler drum level trends

4 结语

本文所述基于单神经元自适应PSD算法的控制方法不依赖精确的对象模型，理论成熟且容易实现。采用该方法后，锅炉汽包液位的动态特性和静态特性均得到有效的改善，并且获得神经网络的自学习能力，可根据锅炉汽包运行工况变化动态整定控制参数，在实际生产中实现了对汽包液位的优化控制，提高了生产效率。

[1] 陈立甲.电站锅炉燃烧系统和汽水系统建模方法的研究[D].哈尔滨：哈尔滨工业大学，2000.

[2] Marsik J.A new conception of digital adaptive PSD control[J].Problems of Control and Information Theory，1983（12）：265-276．

[3] 龚菲，王永骥.基于神经网络的PID参数自整定与实时控制[J].华中科技大学学报：自然科学版，2002，30（10）：69-71． ■