提高中温热力管道系统温度测量准确性的研究

栗鹏飞，杨永平

（陕西理工学院 机械工程学院，汉中 723000）

中温热力管道系统被广泛应用于暖通系统和火力发电系统中，但在中温热力管道系统的研究中非常重要的温度参数，往往得不到准确的测量，有时测量值与热力管道中的实际温度值产生较大的偏差，这严重影响了整个工程系统效率的提高。

由于T型热电偶温度传感器具有热电极均匀性好、热电动势高、反应速度快、测量准确、性能稳定可靠等优点，所以被广泛地应用于中温热力管道系统的温度测量中，但在热力管道系统的实际应用中必须对其进行校正，目前常用的方法有：（1）采用硬件电路进行补偿[1-2]，这种校正方法的成本较高，操作复杂，电路易受外部因素的影响，在实际测量中偏差较大。（2）采用线性拟合[3-6]，这种方法的测量精度较低、误差偏大。

针对中温热力管道系统测温不准确的问题，本文利用最小二乘法对实际测量的热电势-温度数据分段进行一次、二次、三次、四次拟合，然后利用误差原理进行评估，并经过试验验证了该方法能够达到较高的拟合精度且运算速度快。

1 数据的标定

根据中温热力管道系统的实际温度范围，本次试验选取0～400℃作为监测范围。将标准的PT100热电阻温度传感器和被标定的T型热电偶温度传感器放置于可连续变温的温度检定炉中，然后将其同时接入美国MCC公司的USB-2408数据采集模块，通过数据采集模块记录T型热电偶温度传感器随温度变化对应的热电动势，记录的数据通过计算机进行显示，试验系统示意图如图1所示，实测E-T的关系曲线如图2所示。

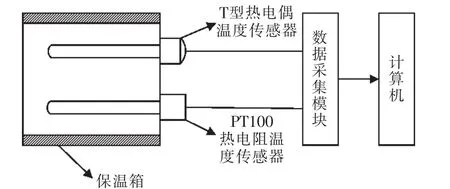
图1 试验系统示意图Fig.1 Schematic of experiment system

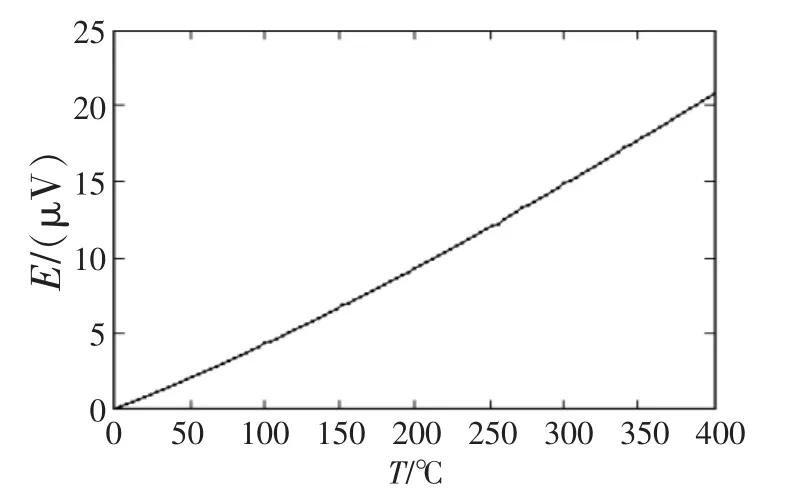
图2 T型热电偶温度传感器E-T的实测数据关系曲线Fig.2 T type thermocouple temperature sensor’E-T relation curve of the actually measured data

2 曲线拟合

2.1 最小二乘法拟合理论

对实测的一组热电势-温度数据（xi，yi）（i=0，1，2，…，n）进行拟合[7]，拟合后的函数为

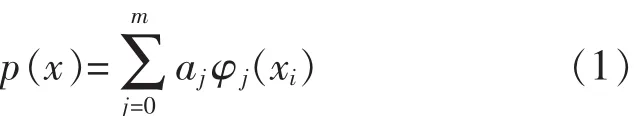
设xi处的误差为

则所有数据点拟合后误差ΔUi的平方和为

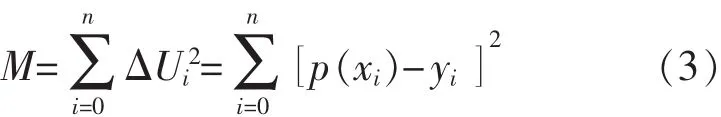
若使 M 取得最小值，需将式（3）分别对 a0，a1，…，am求偏导数，即为

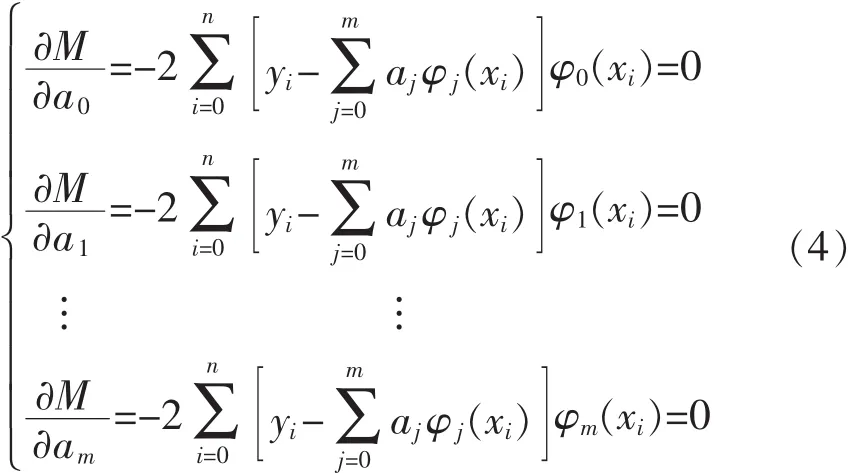
化简可得正规方程为

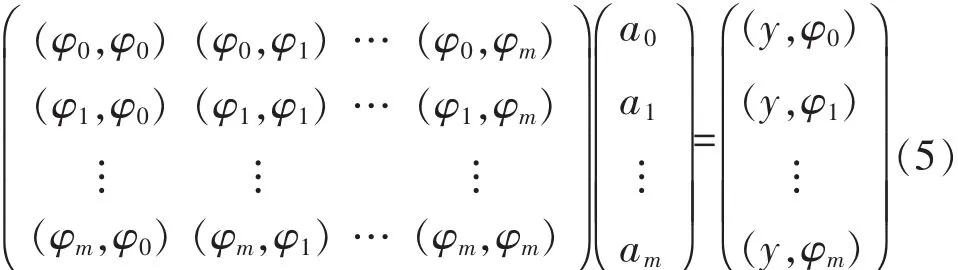
解方程组可得拟合系数 a0，a1，…，am，即可求出拟合多项式 p（x）。

2.2 利用Matlab进行数据拟合

利用Matlab中提供的多项式拟合函数Polyfit（T，E，n），对T型热电偶温度传感器的实际测量的数据分段进行一次、二次、三次、四次拟合[8]，T为实测温度，E为其所对应的电动势，n为拟合次数。拟合后多项式的系数如表1所示。

3 拟合误差评估

3.1 误差评估原理

通常利用绝对误差、算术平均值、标准差来评估拟合多项式的拟合精度[9]。

3.1.1 绝对误差

式中：e为拟合多项式的绝对误差；yi是实际测量的数值；p（xi）是拟合多项式的拟合值；绝对误差e的波动范围越小，则说明拟合多项式的拟合效果越理想。

3.1.2 算术平均值

式中：δ是拟合多项式的算术平均值；n为数据点个数；δ越小，则说明拟合多项式与实测数据的逼近度越高。

表1 T型热电偶温度传感器拟合多项式的系数Tab.1 T type thermocouple temperature sensor’s fitting polynomial coefficient

3.1.3 标准差

式中：σ为拟合多项式的标准差；σ越小，则说明拟合多项式的拟合精度越高。

3.2 拟合结果评估

由图3可以看出T型热电偶温度传感器在4个温度段内进行一次拟合时，绝对误差波动的范围较大，在进行二次、三次、四次拟合时，通过绝对误差不太容易评估出哪种拟合多项式的拟合效果最好。所以，通过对以上3种拟合多项式的算数平均值、标准差进行对比，以便评估最适合T型热电偶温度传感器的校正方程，如表2所示。

由表2可以看出：在4个温度区间内，4次拟合方程的算术平均值、标准差均为最小，由此可得出，在0～400℃范围内，4次拟合方程是T型热电偶温度传感器的最佳校正方程，具体方程如下：

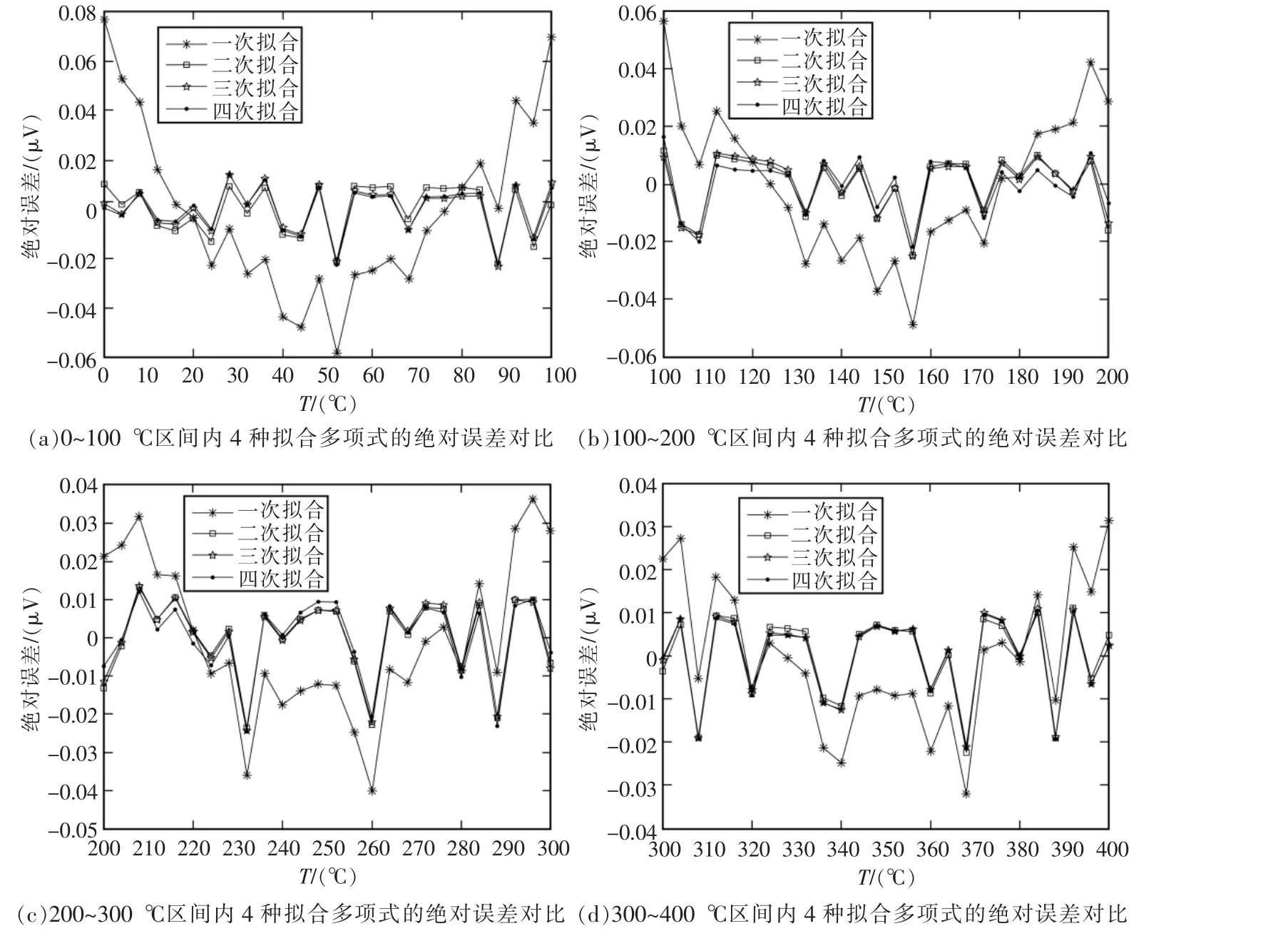
图3 分段拟合的绝对误差对比Fig.3 Comparison of absolute error of the segmented fitting

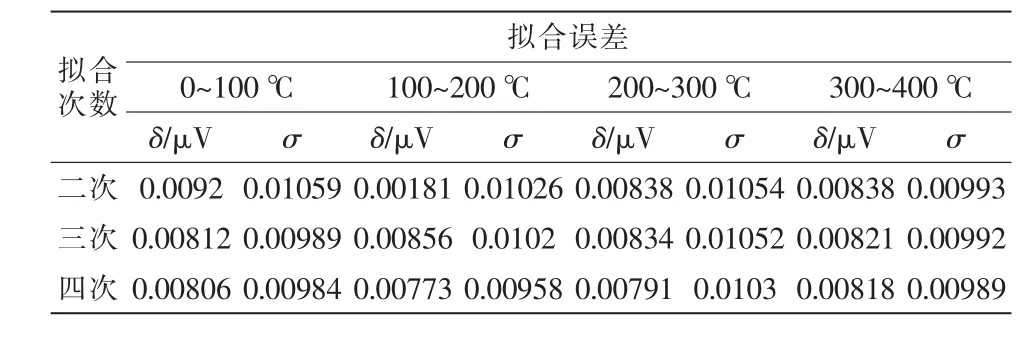
表2 T型热电偶温度传感器分段拟合的拟合误差Tab.2 T type thermocouple temperature sensor’s fitting error of the segmented fitting

4 结语

本文利用最小二乘法对T型热电偶温度传感器的实际测量数据进行拟合，经过对其绝对误差、算术平均值及标准差的比较，得到在0～400℃范围四次拟合的多项式是最适合T型热电偶温度传感器的校正方程。经试验验证，该校正方程在中温热力管道中得到了非常好的应用且对单片机的计算速度要求不高。文中提出的校正拟合的方法，也同样适用于各类热电偶温度传感器的校正拟合。

[1] 张贺丽.一种非线性校正器的设计及应用[J].工业计量，2009，19（4）：34-36.

[2] 王福顺，孙小华，王树涛.基于曲线拟合的土温高精度测量系统[J].农机化研究，2013（8）：158-161

[3] 赵明富，廖强，钟连超，等.热电偶最优化分段最小二乘拟合线性化处理方法[J].计量技术，2004（1）：18-20.

[4] 刘志华.基于最小二乘法的热电偶热电势—温度特性的线性化处理[J].中国教育技术装备，2007（5）：24-25.

[5] 俞阿龙，吴达华.热电偶传感器的一种非线性补偿方法[J].计量技术，2001（8）：21-22.

[6] 瞿江峰.一种基于热电偶的温度测量的线性拟合方法[J].中国西部科技，2010，9（26）：21-23.

[7] 徐明华，张燕新，李志林.数值分析[M].北京：高等教育出版社，2013：124-130.

[8] 李国朝.MATLAB基础及应用[M].北京：北京大学出版社，2011：46-50.

[9] 吴石林，张玘.误差分析与数据处理[M].北京：清华大学出版社，2010：11-17.