基于自适应卡尔曼滤波的动态称重算法的研究

杨 军，李丽宏，周尚儒

（太原理工大学 信息工程学院，太原 030024）

汽车动态称重过程中的运动状态比较复杂，当车辆轮轴驶过秤台时，传感器受到两部分的作用力，一是车辆的稳态载荷，二是车辆的动态载荷（瞬态载荷）。瞬态载荷是影响称重的干扰噪声，也是影响称重准确度的最主要因素[1]。动态载荷产生的因素有很多，如路面凹凸不平、车辆自身的振动、车辆结构的差异、车辆过秤不规则（包括拖磅、跳磅、加减速等）等，这些因素将导致称重数据中信噪比降低、采样数据波形不稳定、车辆重复称量的差异大，尤其是由于车辆过秤速度不同，导致称重数据个数有很大差异，这些问题将导致在使用常规滤波算法处理称重数据时无法保证称量的精度[2]。

卡尔曼滤波是以最小均方误差为最佳估计准则寻求一种递推估计的算法，其基本思想是：采用信号与噪声的状态空间模型，利用前一时刻的估计值和现时刻的观测值来更新对状态变量的估计，求出现时刻的估计值。本文提出的自适应卡尔曼滤波算法中加入了系统误差计算，自适应调节系统的量测噪声[3]，最大限度去除了干扰噪声对系统状态估计的影响。目前采用该算法的仪表已在实际中全面推广应用，称重数据稳定，称重准确度等级达到国家《GB/T 21296-2007动态公路车辆自动衡器》规定的2级秤要求[4]。

1 卡尔曼滤波基本原理

在传统卡尔曼滤波算法中，一般假设系统过程噪声和量测噪声不相关，并且均为零均值的白噪声。但在动态称重系统中的状态空间模型中量测噪声属于时变性质的，其协方差矩阵将不为零。称重系统在受到外部干扰时运动状态可由2部分组成：一部分由已知的运动方程预测出来，另一部分为随机噪声[5]，其状态方程和量测方程可表示为

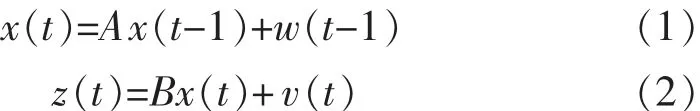
式中：x（t）为状态矢量；z（t）为输出矢量；w（t）和 v（t）分别为系统噪声和量测噪声。

卡尔曼滤波用反馈控制的方法估计过程状态：滤波器估计过程某一时刻的状态，然后以含噪声的测量变量的方式获得反馈[6，9]。卡尔曼滤波的结构图如图1所示。

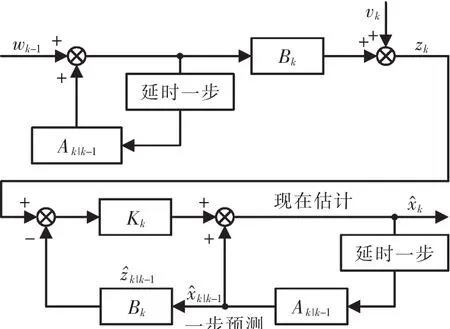
图1 卡尔曼滤波的结构图Fig.1 Structure diagram of Kalman filter

由图1可知，卡尔曼滤波的基本思路是先预测、后校正，可分为两部分：时间更新和量测更新。时间更新包括状态预测和先验误差协方差预测[7-8]，离散表达式为

类似的，预测的观测向量及误差协方差为

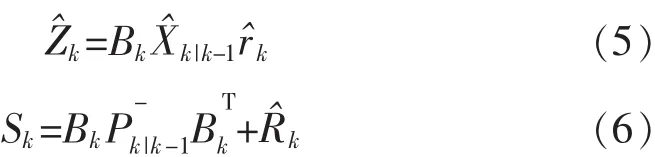
量测更新包括计算卡尔曼滤波器增益和协方差，离散表达式为

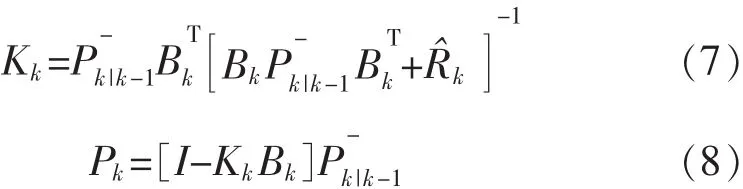
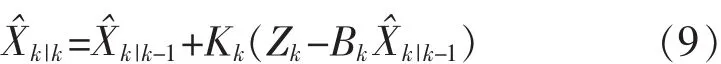
对应的滤波误差协方差更新表达式为

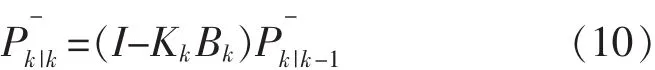
2 量测噪声自适应调节

在卡尔曼滤波器中时变噪声统计估值器可表示为

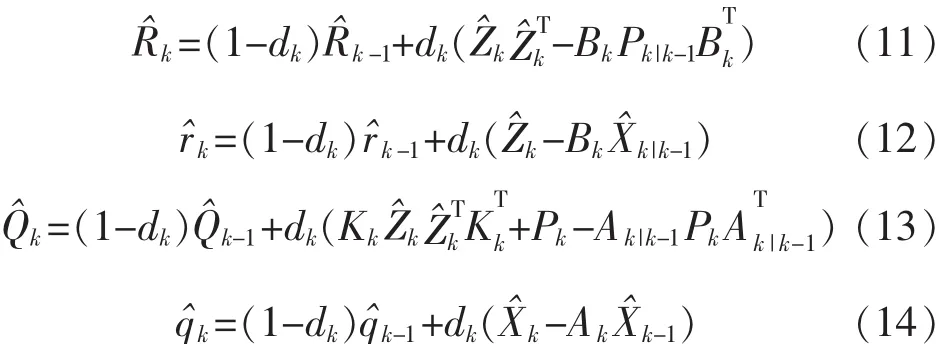
其中，dk=（1-b）/（1-bk+1），0＜b＜1，b 为遗忘因子。

在动态称重系统中，外部干扰噪声w（t）可认为是由车辆、计量平台、地面三者之间组成的耦合系统到时汽车振动的系统噪声[10-11]和因车辆变速行驶、车辆自身结构等引起的随机噪声组成：

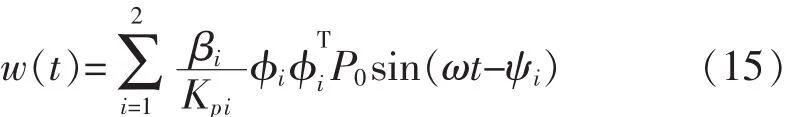
式中：βi为第i阶振幅放大因子；ψi为系统振幅相对激振力的相位差。因此在卡尔曼滤波算法中，系统过程噪声（系统误差）可以认为是定值，即Qk为常量，而由于量测噪声是时变的，在滤波时不能假定Rk为常量，否则将可能导致滤波不准确和滤波发散等后果[12]。

为了得到时变噪声的协方差，本文首先通过最小二乘法对称重数据进行拟合，然后将实际数据与拟合曲线对比，求出时变噪声的协方差，最后通过计算出的量测噪声值带入卡尔曼滤波公式中，对数据进行滤波。

设原始数据阵列为 X= [（x1，y1），（x2，y2），…，（xn，yn）]T，

1122nn

根据动态称重数学模型可设拟合曲线方程y=f（x）的具体表达式（在此不需要考虑干扰噪声）为其中，c0为称重平台的自重，可在实际中测量出来，且为恒值。根据最小二乘法原理，要求测量值yi的偏差的加权平均和最小，即：

式中，C=（c1，c2，c3，c4）， 考虑到各测量值是相互独立的，根据式（17）可得：

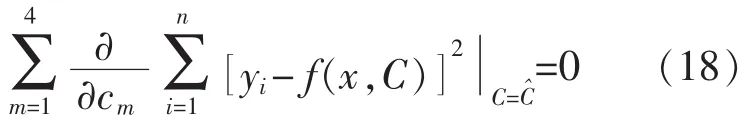
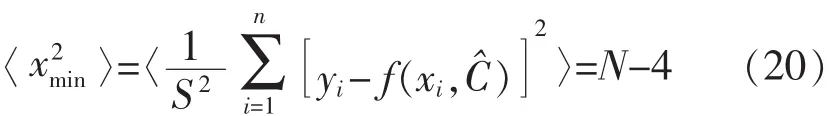
由此可得yi的标准偏差

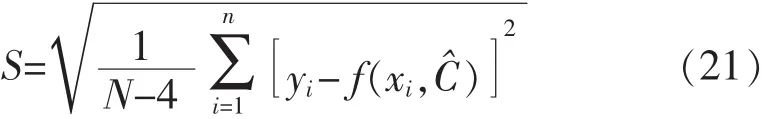
根据S值可以检验拟合曲线是否满足系统要求。

得到拟合曲线后，则原始数据波形上任簇点（xk，yk）到拟合曲线上对应点（xk′，yk′）的距离

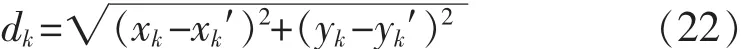
线性化后得到的量测矩阵为

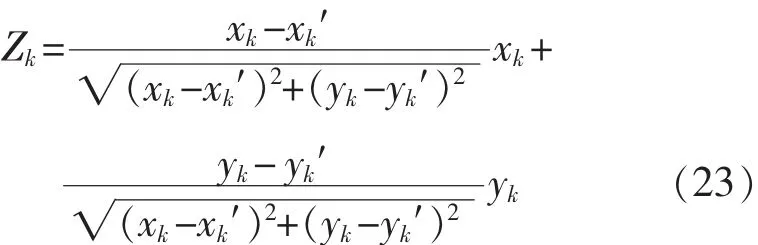
将式（23）带入式（2）中可得到量测噪声：

然后通过量测噪声方差Rk调整卡尔曼滤波增益Kk和量测更新协方差Pk|k。

3 算法效果验证

为了验证滤波算法的性能，将称重仪表采集到的若干车辆过秤时的原始数据通过传统的卡尔曼滤波算法和改进后自适应滤波算法将数据进行了对比处理，随后对该算法进行了多次现场重复实验。

3.1 实验参数输入

由于系统的干扰噪声在滤波算法中进行了处理，因此在对动态称重系统建模时可忽略干扰噪声的影响，即系统模型如式（16）所示，式中参数C需根据采样数据拟合后确定，c0为称重平台自重。为保证算法验证的准确性，系统采样频率和称重平台尺寸与选用采样仪表中的设定值一样。在调试中发现，卡尔曼滤波器的初值协方差P（0）应根据当前仪表采样分度值来确定，这样能减少滤波迭代次数。系统各参数输入如下。

表1 系统参数Tab.1 System Parameters

3.2 实验结果及分析

在实验中发现，当系统量测噪声较小时，两种方法滤波效果均能较好地将干扰噪声滤除，但是对于量测噪声较大的数据，传统的卡尔曼滤波算法有明显的缺陷（滤波程度不够甚至发散）。图2为在量测噪声较大时传统卡尔曼滤波算法和改进后自适应滤波算法的对比图（滤波前后波形在实际中有一定的滞后，为了便于观察现象，在图2中将滤波后前一段无关数据去掉了）。

由图2可知，当原始数据中参杂较为严重的干扰噪声时，传统卡尔曼滤波后的数据仍不能满足实际要求，而使用自适应滤波算法后，数据渐趋平滑，一方面能使系统方便的判断出车轴数量，另一方面能大大提高称重精度。随后将算法改进后的仪表在现场进行了多次试验发现，数据经滤波处理后，称量结果有明显改善；表2所示为10组滤波前后数据对比图，从表中可以看出，滤波处理前，称重精度最大可达到5.81%，而经滤波处理后，称重误差小于±2%。

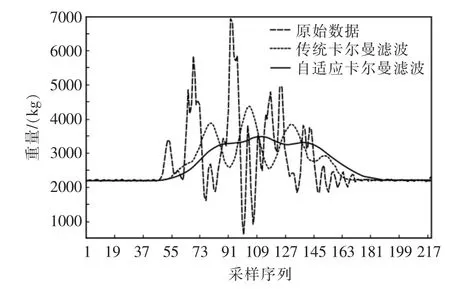
图2 传统卡尔曼滤波算法和自适应卡尔曼滤波算法滤波效果对比图Fig.2 Comparison of filter result between traditional Kalman and adaptive Kalman

表2 滤波前后数据对比Tab.2 Comparison of the data before and after filtering

4 结语

本文讨论了动态称重系统中使用传统卡尔曼滤波算法的局限性，并针对该问题提出了一种自适应滤波算法。该算法是一种自适应调节过程，实时计算系统的量测误差，当系统扰动有明显变化时，在线实时调整卡尔曼滤波器增益及量测更新协方差，而当系统扰动无明显变化时，采用前一阶段的状态进行快速滤波处理。最后通过对原始数据进行分析以及现场试验进行算法验证。试验结果表明，本文提出的自适应卡尔曼滤波算法能明显提高动态称量的准确度以及精度。

[1] 樊旺日.提高动态汽车衡称重精度的算法设计与实现[J].自动化技术与应用，2010，29（7）：47-50，58.

[2] 邵勇强.动态汽车衡存在的问题及对策[J].计量与测试技术，2013，40（1）：7-9.

[3] 赵洪山，田甜.基于自适应无迹卡尔曼滤波的电力系统动态状态估计[J].电网技术，2014，38（1）：3790-3794.

[4] 中国国家标准化管理委员会.GB/T 21296—2007准确度等级[S]，2007.

[5] 章旭景.基于卡尔曼滤波的语音增强算法研究[D].合肥：中国科学技术大学，2009.

[6] 龙礼，张合，唐玉发，等.自适应卡尔曼滤波在地磁姿态检测中的应用[J].兵工学报，2013，34（9）：1155-1160.

[7] 王冲，曾庆军.自适应滤波算法在AUV组合导航中的方法[J].中南大学学报，2014，44（2）：155-160.

[8] 徐经纬，刘士君.交互多模型扩展卡尔曼滤波算法的FPGA实现[J].传感器与微系统，2014，33（1）：11-14.

[9] 李丽宏，赵娜.卡尔曼滤波在动态汽车衡称量中的应用[J].软件，2012，33（3）：25-28.

[10]马晓君，张则，祝思亮.动态电子汽车衡称重系统数学模型的建立[J].佳木斯大学学报，2006，24（3）：379-381.

[11]李丽宏，裴春清，刘军，等.采样点选择对动态汽车衡称量精度的影响[J].中北大学学报，2010，31（1）：19-22.

[12]张文会，韩冰源，马振江.车辆动态称重系统误差产生机理[J].森林工程，2007，23（5）：22-24. ■