雅克比矩阵近似更新的三维装配约束求解研究

丁建完， 侯文洁， 熊 涛

（华中科技大学国家CAD支撑软件工程技术研究中心，湖北 武汉 430074）

雅克比矩阵近似更新的三维装配约束求解研究

丁建完， 侯文洁， 熊 涛

（华中科技大学国家CAD支撑软件工程技术研究中心，湖北 武汉 430074）

提出了三维装配约束求解中雅克比矩阵近似更新的方法。该方法通过对迭代过程中满秩以及行秩秩亏雅克比矩阵进行近似更新，提高了约束求解的效率。首先在非线性迭代求解过程中添加雅克比矩阵及其逆矩阵近似更新的公式；然后给出使用近似更新公式需要满足的限制条件；最后通过对奇异点扰动算法的描述介绍迭代求解过程中雅克比矩阵发生行秩秩亏的处理办法。文中提出的策略与算法已在三维装配约束求解引擎 CBABench中实现，给出的实例表明本文提出的方法效果显著。

约束求解；雅克比更新；几何约束；三维装配；非线性方程

三维装配约束求解技术作为现代CAD系统的关键技术之一，广泛应用于产品造型、装配设计、运动仿真、分子建模等诸多领域[1]。三维装配约束求解的基本任务是求出受约束刚体满足装配约束关系的位置和姿态[2]。对于开环装配约束系统，可依次求解各个刚体上的装配约束实现

约束系统的满足，其求解速度较快；而对于闭环装配约束系统，首先将几何约束映射为约束方程[3]，然后采用速度较快的数值方法对约束方程进行求解，但对于大规模的闭环装配约束系统，现有的数值方法需消耗大量的计算时间，不能满足实际应用的需求，故需对现有的数值方法进行改进。

在三维装配设计中，通过将几何约束映射为约束方程组，并由约束方程组成的方程系统往往是欠约束的[4]，即方程数小于变量数。方程系统的一个基本结构属性是方程与变量的约束依赖关系，这种关系通常采用结构关联矩阵 S来表示[5]，由于结构关联矩阵的稀疏性，可以为矩阵

其中 V1中的顶点对应于矩阵S的行，表示方程；V2中的顶点对应于矩阵S的列，表示变量[6]。根据文献[7]，通过在二部图中不断搜索增广路径，便可以获得二部图的一个最大匹配M，对匹配M进行DM分解[8]，其分解所得子图 G1、 G2和 G3分别对应方程系统中的过约束、欠约束和恰约束部分，其中过约束部分一般无法进行数值求解。鉴于三维装配模型中往往存在欠约束的特性，借助DM分解和文献[9]中提出的符号操作对约束方程系统进行处理，处理后的方程系统由恰约束方程组和欠约束方程组两部分组成。通过Newton-Raphson方法对符号操作后的方程系统进行求解时，无论是对恰约束方程组按 QR分解的方式计算雅克比矩阵的逆矩阵，还是对欠约束方程组按奇异值分解的方式计算雅克比矩阵的广义逆，由于计算逆矩阵的时间复杂度较高，求解的效率都会大大受到影响，尤其是广义逆的计算。就三维装配约束求解而言，求解的效率至关重要，所以高效的求解算法就显得举足轻重[10]，通过采用近似更新雅克比矩阵逆矩阵的方法来减少计算逆矩阵的时间复杂度[11]，就成为提高求解效率的重要手段之一。

1 经典的Newton-Raphson迭代

首先给出求解非线性方程组经典的Newton-Raphson迭代[12]，考虑非线性方程组(1)。

J（k）表示方程组在点 x（k）处的雅克比矩阵，表示方程组在点 x（k）处的值。

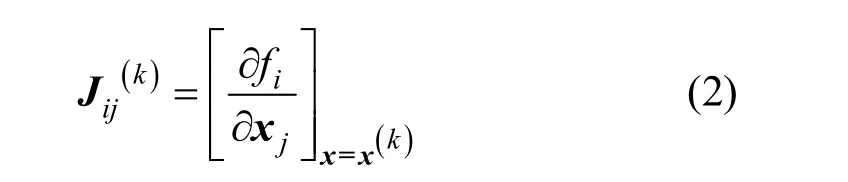
对于非线性求解的第 k （k = 1,2,…） 次迭代，通过求解线性方程组(3)得出第 k次迭代的修正变量 δ（k）。

方程组解的估计值变为

2 雅克比矩阵及其逆矩阵的近似更新

式(1)～(4)为经典的 Newton-Raphson迭代，一次迭代需要计算雅克比矩阵 J（k）和矩阵 J（k）的逆矩阵 H（k）。对于满秩矩阵 J（k）， H（k）的计算需借助QR分解的方式求得，计算的时间复杂度为O(n3)，如式(5)。

而欠约束的三维装配模型通过模型映射得到的方程系统中存在雅克比矩阵为奇异的方程组，如式(6)。

该方程组无法借助QR分解的方式计算雅克比矩阵的逆，为使迭代求解能够继续，取

无论雅克比矩阵是否满秩，若在每次迭代求解中按上述方法计算雅克比矩阵的广义逆，求解的效率都会大大受到影响。为了提高求解的效率，降低计算逆矩阵的时间复杂度，第k+1次迭代中所使用的逆矩阵 H（k+1）是通过近似更新H（k）得到的，该方法的时间复杂度为 O(n2)，下面给出近似更新的公式。

由式(3)和式(5)，我们得出第k次迭代修正变量 δ（k）的计算式(8)。

式(10)中 F（x）表示方程组残差的平方和，参见式(11)。

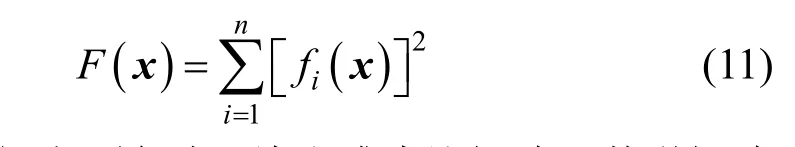
根据上面各式，给出雅克比矩阵及其逆矩阵近似更新的公式[11]。

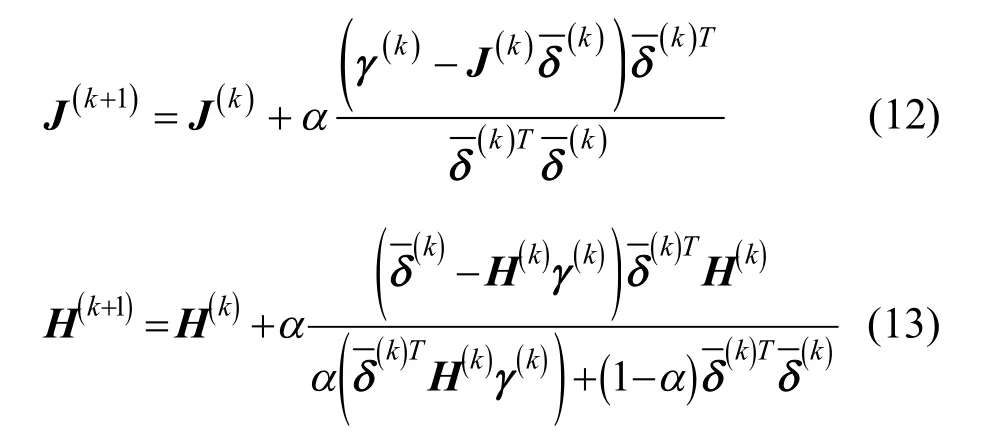
根据工程实际应用，式(12)和(13)中参数α的取值可以为1或0.8，绝大多数情况下取 α= 1，得到式(14)和(15)。

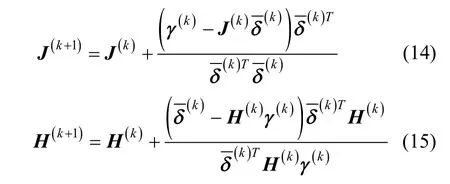
为避免式(15)中分母的数值过小，导致近似更新 H（k+1）时发生奇异，当满足式(16)时，取α= 0.8。

下面通过式(17)～(20)证明由近似更新得到的雅克比矩阵是满足求解要求的，假定在点x（k）处存在矩阵 J*，矩阵 J*满足式(17)。

根据式(12)和(17)可得：

由式(18)可得：

当式(20)满足时，上式中的等号成立。

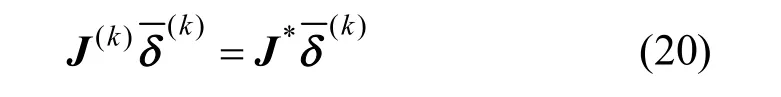
根据上面的描述，由式(19)可知，通过近似更新得到的雅克比矩阵是满足迭代求解要求的。下面我们考虑舍入误差对于近似更新的影响，基本上每次迭代都需要近似更新逆矩阵H，每次更新都会引入一些误差。由式(14)和(15)，得出式(21)。

综上所述，结合式(12)～(21)，近似更新有下面几个优点：①计算复杂度为 O (n2)；②如果H(k)是 J(k)的逆矩阵，那么 H(k+1)也是 J(k+1)的逆矩阵；③舍入误差收敛。但近似更新也存在下面的不足：①若不加限制条件地使用近似更新公式，在迭代多次后，通过近似更新得到的逆矩阵与准确值之间就可能相差过大，严重影响求解效率；②迭代求解过程中雅克比矩阵的秩亏对近似更新的准确性影响较大。下面通过给出使用近似更新的限制条件和奇异点扰动算法来解决近似更新存在的不足。

3 近似更新的限制条件

非线性方程组往往需要迭代求解，在逆矩阵多次近似更新后，由于步长不合适、舍入误差积累等原因的存在，造成多次近似更新后的逆矩阵与准确值偏差过大，严重影响了求解的效率和准确性，所以在迭代求解的过程中必须对逆矩阵的近似更新添加限制条件。

以非线性求解的第 k（k = 1,2,…） 次迭代为例，首先定义几个变量：fnorm和 fnorm1分别为方程组 f( x)≡ fi(x1,x2,…,xn)=0, i= 1,2,…,mm ≤n在 x(k)和 x(k)+δ(k)处残差的 Euclidean范数；actred为比例变量。

结合式(22)～(24)，给出使用近似更新公式的限制条件。

当满足条件表达式(25)时，使用近似更新公式计算雅克比矩阵的逆矩阵，否则，按常规方法重新计算逆矩阵。该限制条件的提出提高了求解的效率与准确性，使近似更新公式在工程实际中的应用成为可能。

4 奇异点扰动

迭代求解过程中Jacobian矩阵行秩的秩亏对近似更新的影响较大，易造成迭代求解的失败，导致矩阵秩亏的原因有下面3个方面：①欠约束方程组导致雅克比矩阵秩亏；②奇异点导致雅克比矩阵秩亏[14]；③前面两个条件的综合作用导致雅克比矩阵的进一步秩亏。

图1 雅克比矩阵出现秩亏的情况

图1中左图表示两个几何点P1(x1, y1, z1)和P2(x2, y2, z2)之间添加距离为L的约束；右图表示四连杆机构中的“死点”位置。对应于左图，方程结构导致雅克比矩阵行秩秩亏，同时当 P1和P2的坐标均为(0, 0, 0)时，该特殊的数值点（奇异点）导致雅克比矩阵进一步秩亏；对应于右图，特殊的几何元素形位（“死点”）导致雅克比矩阵秩亏。对于由特殊的数值点造成的矩阵秩亏，可利用奇异点扰动的方法进行处理。下面给出奇异点扰动算法：

Step 1令 i ←0， d1 , d2←0；

Step 2计算非线性方程组f (x)在x处的雅可比矩阵J，并对矩阵J执行QR分解。如果矩阵R中对角线元素为零的个数等于由于方程结构导致雅克比矩阵的秩亏数，返回；

Step 3若 i =0，令 d 1 ← 1e-5，i ←i+1；若 i ＞0，令 xi=xi-d2， i ←i+1；

Step 4如果i大于方程的个数， i ←1，若d 1＞0， 令 d 1← -d1； 若 d1 ≤ 0， 令

Step 5如果返回；

Step 6d2←max(1.0,)*d1，xi=xi+d2，转Step2。

上述扰动算法包括正负两个方向的扰动，若只做单方向的扰动，不能保证结果的正确性[15]。此外在进行奇异点扰动时，扰动变量的取值不能采用绝对扰动量，而应采用相对扰动量，以避免不恰当的扰动使方程无解或得出的解与初值偏离过大。相对扰动量的大小对应上述算法中的步骤4，相对扰动量序列为±1e-5、±1e-4、±1e-3、±2e-3、±4e-3、±8e-3、±16e-3、±32e-3、±64e-3、±128e-3，该扰动序列在实际应用中取得了较好的效果。奇异点扰动可以对求解过程中雅克比矩阵秩亏的问题进行处理，保证近似更新的准确性，并提高迭代求解的效率。

5 实例验证

本节以挖掘机的三维装配模型为例，验证三维装配约束求解引擎 CBABench[3]对于该装配模型求解的效率和准确性。不考虑连接部件，该模型包含的主要部件有：固定底座 B0，动臂 B1，动臂油缸B2和B3，动臂油缸活塞杆B4和B5，铲斗油缸 B6及其活塞杆B7，摇杆B8和 B9，连杆B10和推杆 B11，铲斗托 B12和铲斗 B13。图 2(b)为这些部件的装配结果。

图2中，三维装配模型由共轴约束CoiLL(B0, B1)、CoiLL(B0, B2)、CoiLL(B0, B3)、CoiLL(B2, B4)、CoiLL(B3, B5)、CoiLL(B1, B4)、CoiLL(B1, B5)、CoiLL(B0, B6)、CoiLL(B6, B7)、CoiLL(B7, B8)、CoiLL(B1, B8)、CoiLL(B8, B10)、CoiLL(B10, B11)、CoiLL(B11, B12)、CoiLL(B1, B9)、CoiLL(B9, B11)、CoiLL(B12, B13)；共面约束 CoiFF(B0, B1)、

CoiFF(B1, B4)、CoiFF(B1, B5)、CoiFF(B7, B8)、CoiFF(B1, B8)、CoiFF(B8, B10)、CoiFF(B10, B11)、CoiFF(B1, B9)、CoiFF(B12, B13)；共点约束CoiPP(B12, B13)组成，其中CoiLL表示共轴约束、CoiFF表示共面约束、CoiPP表示共点约束。采用前言中介绍的符号的方法对该几何约束图分解，可以发现刚体B0～B12构成耦合闭环子图Gs，采用螺旋理论[16]将 Gs内的几何约束组合转换成运动副约束，有转动副J1(B0, B1)、J2(B1, B4)、J3(B1, B5)、J4(B1, B8)、J5(B1, B9)、J6(B1, B12)、J7(B7, B8)、J8(B8, B10)、J9(B10, B11)和圆柱副J10(B0, B2)、J11(B0, B3)、J12(B0, B6)、J13(B2, B4)、J14(B3, B5)、J15(B6, B7)、J16(B9, B11)、J17(B11, B12)，则可得到耦合闭环子图Gs对应的运动副约束图Gk，如图3所示。分析运动副约束图Gk中所有运动副的特征参数可知，不考虑圆柱副J13(B2, B4)、J14(B3, B5)、J15(B6,

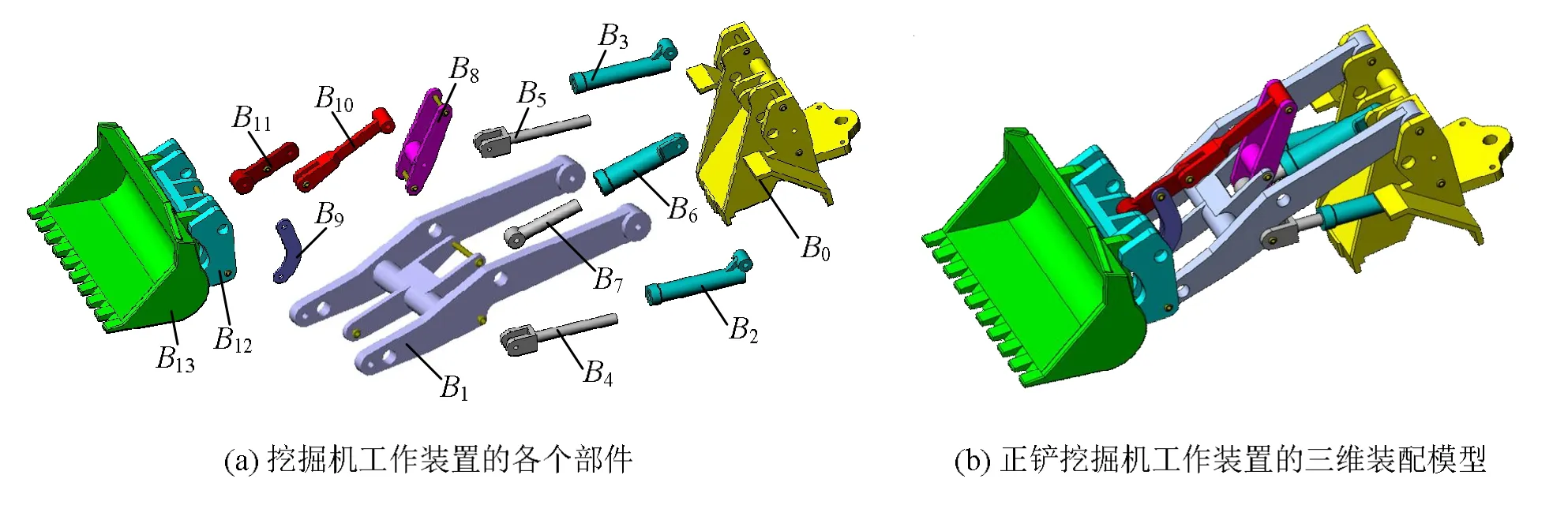
图2 挖掘机三维装配模型

图3 正铲挖掘机工作装置的约束图

B7)、J16(B9, B11)和J17(B11, B12)的约束，Gk中的所有刚体仍然在相互平行的平面内运动。显然，Gs为可投影求解的耦合几何约束闭环。这样，挖掘机工作装置三维几何约束系统可投影映射为图 4所示的二维几何约束系统，包含的几何约束有：点点距离约束和点点重合约束点在线上约束共15个约束方程和17个求解变量。

图4 二维几何约束系统

在不使用规划分解的情况下采用本文介绍的方法对该约束方程系统直接进行求解，设置求解精度为1e-5，迭代求解过程中共计算矩阵的逆135次，其中雅克比矩阵近似更新的计算次数为118次，其余17次因为不满足近似更新的限制条

件，而进行了MP广义逆的计算，奇异点扰动3次。对比本文中提出的方法，当采用经典的Newton-Raphson法对其进行迭代求解时，共计算MP广义逆164次、奇异点扰动5次（表1）。

表1 近似更新法与经典Newton-Raphson法效果对比（次数）

由上述实验结果可知：迭代过程中大量MP广义逆的计算被近似更新所替代，减小了计算时间；限制条件和奇异点扰动算法的引入，降低了总的迭代次数，求解的效率得到了明显的提升。

6 结 论

三维装配约束求解效率的提高在工程实际中具有重要的意义，本文对求解过程中雅克比矩阵的近似更新、使用近似更新公式的限制条件以及求解过程中会对近似更新造成较大影响的雅克比矩阵秩亏进行了深入研究，提出了一套有效的策略，并给出了相应的算法。本文的主要贡献在于：①给出秩亏雅克比矩阵及其逆矩阵近似更新的公式，提高了三维装配约束模型求解的效率；②结合近似更新公式在实际应用中存在的问题，提出了使用近似更新公式的限制条件，使近似更新在工程实际中的应用成为可能；③奇异点扰动算法的完善，保证了近似更新的准确性。本文提出的策略与算法已在三维装配约束求解引擎CBABench中实现，效果显著。

[1] 高小山, 蒋 鲲. 几何约束求解研究综述[J]. 计算机辅助设计与图形学学报, 2004, 16(4): 385-396.

[2] 黄学良, 陈立平, 王波兴. 求解三维装配约束闭环的投影变换方法[J]. 计算机辅助设计与图形学学报, 2010, 22(12): 2138-2146.

[3] Peng Xiaobo, Lee K W, Chen Liping. A geometric constraint solver for 3-D assembly modeling [J]. The International Journal of Advanced Manufacturing Technology, 2006, 28(5-6): 561-570.

[4] Owen J C. Algebraic solution for geometry from dimensional constraints[C]//Proceedings of the ACM Symposium on Solid Modeling Foundation, Austin, TX: ACM Symposium on Solid Modeling Foundation, 1991: 397-407.

[5] Barton P I. Structural Analysis of Systems of Equations [R]. Massachusetts Institute of Technology. Department of Chemical Engineering, 1995: 2-5.

[6] 肖位枢. 图论及其算法[M]. 北京: 航空工业出版社, 1993: 124-126.

[7] Karp R M, Hopcroft J E. An n5/2algorithm for maximum matchings in bipartite graphs [J]. SIAM Journal of Computing, 1973, 2(4): 225-231.

[8] Bliek C, Neveu B, Trombettoni G. Using Graph Decomposition for Solving Continuous CSPs[C]//Proceedings of the Principles and Practice of Constraint Programming, Pise, Italy, 1998: 102-116.

[9] Serrano D. Constraint Management in Conceptual Design [D]. Ph.D. Thesis. Massachusetts Institute of Technology, Dept. of Mechanical Engineering, 1988: 52-72.

[10] Zhu Zhenmin, Liu Degui, Li Shoufu. A class of fast algorithm in real-time simulation [J]. Journal of Systems Engineering and Electronics, 1999, 10(4): 10-20.

[11] Powell M J D. A method for minimizing a sum of squares of nonlinear functions without calculating derivatives [J]. Computer Journal, 1965, 7: 303-307.

[12] Broyden C G. A class of methods for solving nonlinear simultaneous equations [J]. Mathematics of Computation, 1965, 19: 577-593.

[13] Ben-Israel A, Greville T N E. Generalized inverses: theory and application [M]. 2nd Edition. New York: Springer Verlage, 2003: 41-43.

[14] Haug E J. Computer aided kinematics and dynamics of mechanical systems: basic method [M]. Boston: Allyn and Bacon, 1989: 104-111.

[15] Li Yantao, Hu Shimin, Sun Jiaguang. On the numerical redundancies of geometric constraint systems[C]//Proceedings of the IEEE 9th Pacific Conference on Computer Graphics and Applications, Tokyo, 2001: 118-123.

[16] 黄 真, 赵永生, 赵铁石. 高等空间机构学[M]. 北京: 高等教育出版社, 2006: 61-75.

Research on 3D Assembly Constraint Solving with Approximate Update Formula of Jacobian Matrix

Ding Jianwan, Hou Wenjie, Xiong Tao
(National CAD Support Software Engineering Research Center, Huazhong University of Science and Technology, Wuhan Hubei 430074, China)

A new method of approximately updating Jacobian matrix during 3D assembly constraint solving is proposed in this paper. This method principally improves the efficiency of constraints solving based on the approximate update of Jacobian matrix. First, an approximate update formula of Jacobian matrix and its inverse matrix are inserted to the non-linear iterative solution process. After that, the indispensable constraint is put forward, which must be satisfied when using the formulas above. At last, a solution handling row rank defect of Jacobian matrix is introduced via disturbance algorithm description. The methodology presented is implemented in a 3D assembly constraint solving engine, named CBABench. An example given at the end of this paper shows that the method has achieved a considerable effect.

constraint solving; Jacobian update; geometric constrains; 3D assembly; non-linear equations

TP 391

A

2095-302X (2014)03-0368-06

2013-08-27；定稿日期：2013-11-27

国家科技支撑计划资助项目（2012BAF16G02）

丁建完（1975-），男，湖南桃江人，副教授，博士。主要研究方向为约束系统规划分解与数值求解、多领域系统统一建模与仿真等。E-mail：dingjw@hust.edu.cn

侯文洁（1990-），女，河南信阳人，硕士研究生。主要研究方向为几何约束求解，多领域系统统一建模与仿真。E-mail：houwj@hust.edu.cn