基于全要素生产率视角的深圳经济运行质量实证研究

林德钦

（清华大学深圳研究生院 社会科学与管理学部，广东 深圳 518055）

基于全要素生产率视角的深圳经济运行质量实证研究

林德钦

（清华大学深圳研究生院 社会科学与管理学部，广东 深圳 518055）

通过构建总量生产函数模型，对深圳市1979—2010年的全要素生产率进行了测算，并对这一期间深圳经济运行质量进行实证分析。结果表明：深圳经济全要素生产率呈逐年递增的趋势，但其对深圳经济增长的平均贡献率只有19.70%，要素投入对深圳经济增长的平均贡献率则高达79.18%，深圳经济的运行质量不佳，仍处于粗放型发展阶段。经济的快速发展是以大量的要素投入为代价的，技术进步因素所起的作用较小。

全要素生产率；索洛余值；深圳特区；运行质量

一、引言

改革开放30年来，作为我国改革开放试验田的深圳市经济取得了举世瞩目的成就和发展，地区生产总值以超过20%的速度飞速增长。然而，深圳经济取得如此高的发展成就在很大程度上是国家给予的各种政策优惠和大量的要素投入所带来的，随着改革的不断深入和经济的发展，深圳市经济面临的“四个难以为继”的约束也愈发明显。正因为如此，在深圳市“十二五”规划中，明确提出“深圳质量”这一概念，重点将转变经济发展方式、优化产业结构、节约资源、保护环境以及创造经济发展质量作为其主要目标。

经济的增长既包括数量的增长，也包括运行质量的提高，应该是二者的统一。其中，数量的增长指的是投入要素的增加引起的经济增长；圆形质量的提高则指的是非要素投入以外因素的改善引起的经济增长。而全要素生产率指的是各种投入要素以外的因素对经济增长的贡献，恰好可以用以表征经济运行质量好坏。

基于以上认识，对深圳经济全要素生产率进行测算并据此就其经济运行质量进行实证研究具有一定的理论和现实价值。

二、相关文献综述

首先运用定量方法对经济增长进行研究的是芝加哥大学经济学教授P.H.Douglas和数学家C.W.Cobb，他们于1928年首次将经济数学模型引入到生产的分析中来，提出了著名的“柯布—道格拉斯生产函数”即C—D生产函数。[1]荷兰经济学家J.Tinbergen（1942）则将时间趋势引入到生产函数中来，并第一次提出了全要素生产率的概念。[2]以上述研究为基础，美国经济学家R.M.Solow（1957）提出了总量生产函数的概念，并明确将全要素生产率定义为总产量增长率扣除要素投入增长对其贡献率之后的“余值”，并首次运用此方法对全要素生产率进行了测算。[3]郭庆旺，贾俊血（2005）运用“索洛余值法”对我国1979—2004年的全要素生产率进行了测算，并对我国经济和全要素生产率增长的源泉进行了分析。[4]徐瑛，陈秀山，刘凤良（2006）则将产业结构、人力资本等因素引入中国经济全要素生产率的分析中来，并据此对我国1987—2003年的全要素生产率进行了测算。[5]徐现祥（2000）则通过构建C D生产函数，对我国1980—1997年的全要素生产率进行了测算，并提出了经济增长方式的判断标准。[6]云鹤，吴江平，王平（2009）则将经济结构、人力资本因素引入到总量生产函数中来，测算我国1978—2005年的全要素生产率，并对我国经济增长方式的转变进行了实证分析。[7]

三、数据来源及处理

1.数据来源

本文从2011年《深圳统计年鉴》以及《中国统计年鉴》中获得深圳市1979—2010年地区生产总值GDPt、资本投入量Kt以及劳动投入量Lt等相关数据资料。

2.数据处理

由于地区生产总值GDPt、资本投入量都是按照当年的价格来计量的，为了确保各年之间数据的可比性和统计口径的一致，需要进行价格调整，换算成按照不变价格计量的数据。

对于深圳市地区生产总值序列，以1978年为基期进行指数平减，换算成以1978年不变价格计量的地区生产总值。理论上而言，应该用资本流量作为资本投入的衡量指标，然而，资本流量方面的数据往往难以获得。因此，通常将资本存量作为资本投入的近似代替，并按照Goldsmith于1951年提出的永续盘存法进行调整：

其中，Kt和Kt1分别代表第t和t1年的资本存量，It代表第t年的投资额（基于数据可获得性考虑，本文中采用深圳市历年全社会固定资产投资额作为代替指标，并按照全国固定资产投资价格指数进行平减，换算成以1978年不变价格计量的实际投资额）。 代表折现率。关于基期（1979）年深圳市资本存量的计算，本文采用覃武，谭砚文（2010）所介绍的方法。[8]即用深圳市与广东省1979年固定资产投资额之间的比值再乘以广东省1979年的资本存量。计算公式如下：

而有关广东省1979年的资本存量数据，可以直接从周苗苗，周光南（2004）的计算结果中获得。[9]

四、模型构建及实证分析

1.模型构建

为了运用“索洛余值法”测算出深圳经济运行的全要素生产率，首先需要构建总量生产函数。然而，在传统的C D生产函数中，全要素生产率被假定为一常数，难以反映其随时间而变化的特点。因此，本文引入时间趋势项以刻画全要素生产率随时间变化的特征，构建的总量生产函数形式为：

在（1）式中，Yt代表深圳市各年以1978年不变价格计算的GDPt，A为常数，t表示时间，Kt为第t年的资本投入量，Lt为第t年的劳动投入量则分别代表资本投入和劳动投入的产出弹性。

通过普通最小二乘法，便可以得到（2）式中各个参数的估计值，并计算得到劳动投入的产出弹性系数全要素生产率TFPt可以通过下式计算得到：

为了测算因素对深圳经济增长的贡献率的大小，先对（1）式两边同时取对数，然后对t求微分，可以得到：

如果用Gy、Gtfp、Gk与Gl分别表示总产出Yt的增长率、全要素生产率TFPt的增长率、资本投入量Kt的增长率以及劳动投入量Lt的增长率，则（4）式可以进一步简化为：

（5）式两边同时除以Gy，可得：

通过全要素生产率的增长以及投入要素的增长对总产出增长贡献率的相对大小比较，可以对深圳经济运行质量的情况进行分析和判断。令则经济运行质量的判断依据可以表述为：

2.实证分析

运用eviews5.0软件对（2）式进行回归，得到回归方程为：

由以上回归结果可以看出，虽然各参数估计值的经济意义合理，t统计量检验表明其显著异于0。但是，DW统计量的取值（DW=0.821594）小于临界值的下限（DL=1.244）。这表明，回归残差存在着正相关关系，回归残差图也能体现这种正相关关系。回归残差图如图1所示：

图1 回归残差序列图

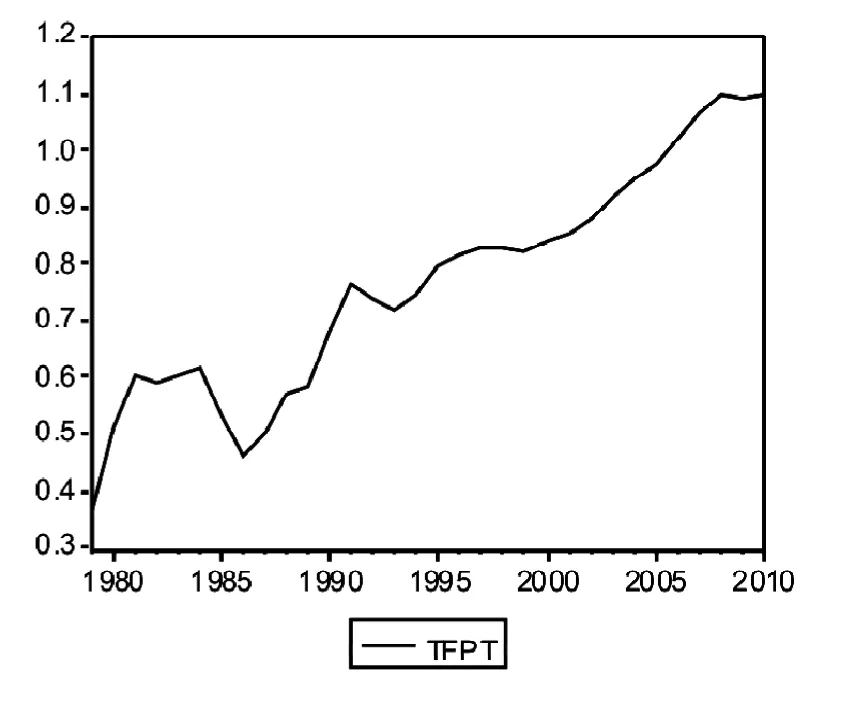
图2 1979—2010深圳TFP变化趋势图

为了消除上述回归方程中残差序列的正相关性，以残差et作为被解释变量，以其滞后值作为解释变量进行回归分析。经过多次尝试和比较后发现，以滞后1阶和滞后2阶的残差值作为解释变量的回归效果最为明显。回归结果如下：

根据以上残差序列的自回归分析结果，运用Cochrance-Orcutt迭代法消除残差序列的自相关性，得到新的回归结果为：

（7）式中各参数估计值的t统计量均显著，残差序列的相关性亦得到了消除，拟合优度值显示模型的整体拟合效果良好，这些均表明本文构建的总产生产函数较为合理。由回归方程（7）可以看到，资本投入的产出弹性为0.980258，劳动投入的产出弹性为0.019742。

根据（7）式所得到的参数估计值以及（3）式所示的全要素生产率TFP的计算公式，可以计算得到深圳经济1979—2010年间的全要素生产率如表1所示：

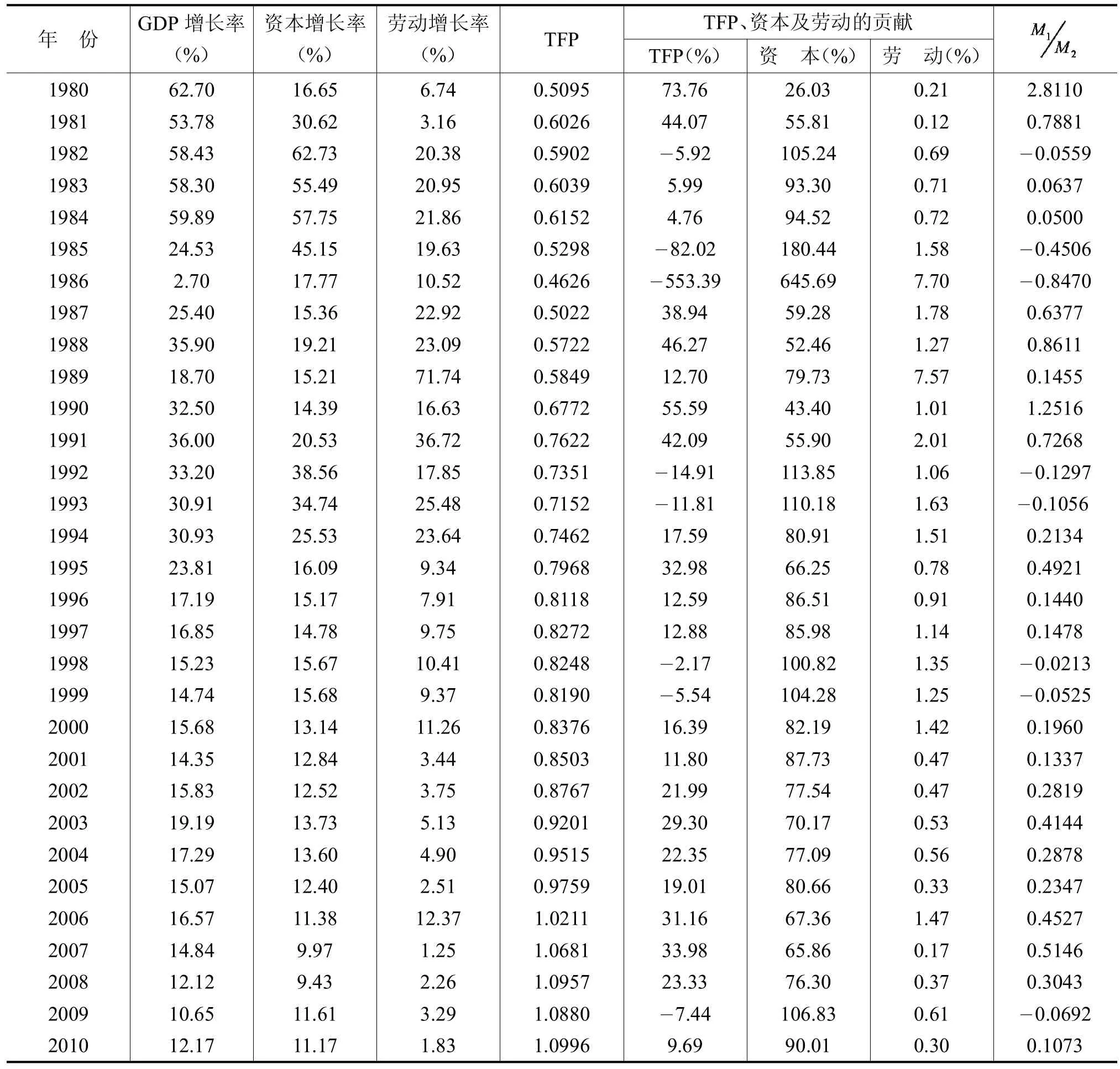
表1 深圳经济运行质量相关指标统计表

根据表1第5列所示的深圳经济1979—2010年的全要素生产率数据，以年份为横坐标，全要素生产率为纵坐标，建立直角坐标系，可以得到全要素生产率随时间变化的趋势图，如图2所示。

由图2可看出，1979—2010年，深圳经济运行的全要素生产率总体呈现出上升的趋势。只是在1984—1986年出现明显的下降趋势，并于1986年下降至相对的低点位置。究其原因，可能是深圳市政府1985年之前的基础建设投资过多，导致市财政收入入不敷出，透支巨大，这也促使深圳市的城市建设在1986年进行了一次重大的调整。[10]自此以后，深圳经济运行的全要素生产率呈现逐步上升的趋势，并于2010年达到最高点。

为了同时展现TFP增长率、资本投入增长率、劳动投入增长率与深圳GDP增长率之间的相互关系，可以年份为横坐标，增长率作为纵坐标，建立平面直角坐标系，并将TFP增长率、资本投入增长率、劳动投入增长率与深圳GDP增长率随时间变化的趋势展示于同一张图中，如图3所示。

根据图3可以明显地看出，TFP增长率及资本投入增长率与深圳GDP增长率随时间变化的趋势具有较高的同步性，显示出两两之间具有较强的正相关关系。相反，劳动投入增长率与深圳GDP增长率随时间变化趋势的同步性较差，说明二者之间的相关性较弱。

虽然图3表明TFP增长率及资本投入增长率与深圳GDP增长率随时间变化的趋势之间具有较强的相关性，但是二者对深圳GDP增长的贡献率存在着较大的差别。根据表1所示的数据，剔除1985年和1986年这两年的特殊数据以后，可以计算得出1980—2010年，深圳GDP年均增长率达到了25.48%。其中，全要素生产率TFP增长率对深圳GDP增长率贡献平均为19.70%；资本投入增长率对深圳GDP增长率贡献的平均为79.18%；而劳动投入增长率对深圳GDP增长率贡献则较小，平均而言只有1.34%。由此表明，深圳经济近30年持续飞速发展主要是以大量的资本投入为代价的，其次是技术进步因素，劳动投入所产生贡献则最低。根据本文所给出的判断标准，平均而言，深圳经济目前仍然处于粗放型发展的阶段。

同理，为了分析1979—2010年深圳经济运行质量随时间变化的趋势，可以将表1最后一列所示数据以图形的形式展现出来，如图4所示。

图3 深圳经济GDP、TFP、Kt与Lt变化趋势图

图4 经济运行质量判别指标变化趋势图

五、结论与建议

本文通过构建一个带时间趋势的总量生产函数模型，考察了深圳市经济全要素生产率TFP的测算，分析了TFP增长率、资本投入增长率以及劳动投入增长率对深圳GDP增长的贡献，并设置TFP增长率对GDP增长率贡献与要素投入增长率对GDP增长率贡献的比值作为评价指标，考察深圳1979—2010年间经济运行质量随时间变化的特征。根据本文实证分析所得结论，针对深圳的现实情况，欲改变深圳经济发展主要依靠高资本投入拉动的局面，提高深圳经济运行的质量，首先，完善创新体系，增强核心技术的自主创新能力，加快推进创新型城市建设。其次，进一步优化、调整经济结构，大力发展金融、物流等现代服务业，实现高技术产业和现代服务业双轮驱动经济发展的格局。最后，大力发展高等教育和职业技术教育，培养高层次人才，提高劳动者素质，为深圳经济发展提供人才保障和智力支持。

[1]Charles W.Cobb，Paul H.Douglas.A Theory of Production.The American Economic Review，1928，（18）：139-165.

[2]J.Tinbergen.Professor Douglas’s Production Function.Review of the International Statistical Institute，1942，（10）：37-48.

[3]R.Solow.A Contribution to the Theory of Economic Growth.Quarterly Journal of Economics，1956，（70）：65-94.

[4]郭庆旺，贾俊血.中国全要素生产率的估算：1979—2004[J].经济研究，2005，（6）：51-60.

[5]徐瑛，陈秀山，刘凤良.中国技术进步贡献率的度量与分解[J].经济研究，2006，（8）：93-103.

[6]徐现祥.我国经济增长方式转变的实证分析[J].上海经济研究，2000，（3）：27-32.

[7]云鹤，吴江平，王平.中国经济增长方式的转变：判别标准与动力源泉[J].上海经济研究，2009，（2）：11-18.

[8]覃武，谭砚文.深圳经济增长因素分析：1979—2007——基于全要素生产率视角[J].城市发展研究，2010，（3）：97-102.

[9]周苗苗，周光南.广东经济路在何方[J].中山大学研究生学刊（社会科学版），2004，（25）：86-93.

[10]李罗力，郭万达，张玉阁.定位深圳的全面创新与和谐发展[M].北京：中国经济出版社，2006.

[责任编辑：辛晓莉]

F127.652

A

1674-3288（2014）02-0023-05

2014-03-28

深圳市社会科学重点规划课题“深圳市率先实现经济增长方式根本转变战略研究”（115A002）

林德钦（1983-），男，清华大学深圳研究生院社会科学与管理学部助理研究员，数量经济学博士研究生，研究方向：金融计量、宏观经济建模。