“数字信号处理”课程的教学实践与体会*

孔令杰

（菏泽学院物理系，山东菏泽 274015）

引言

随着计算技术和信息科学的迅速发展，数字信号处理的理论与应用得到突飞猛进的发展，业已形成了一门极其重要的学科.

“数字信号处理”课程作为高等学校电子信息类专业一门重要的专业基础性课程，是理论与实践、原理与应用紧密结合的课程［1］.学习与该课程相关的理论知识，不仅能够使学生掌握数字信号处理领域中常用的基本理论、基本技能和基本方法，也能够为学生学习后续课程和应用数字信号处理技术奠定坚实的基础.但在学习过程当中，大部分学生发现该课程中公式多且复杂、概念抽象且难以理解与掌握，普遍产生了厌学和畏难情绪［2］.因此，如何帮助学生理解与掌握“数字信号处理”课程中的基本概念、基本原理及其基本分析方法，提高学生综合应用所学知识解决实际问题的能力，俨然成为该课程教学任务中所要解决的关键性问题.

鉴于此，该文提出在传统教学的基础上，应将Matlab仿真软件引入到“数字信号处理”课程的教学中，通过结合Matlab仿真软件的实践性教学，使学生从繁琐复杂的数学运算推导中解脱出来，将学习的重点放在对“数字信号处理”课程的基本概念与基本方法的理解上，以期提高学生分析问题和解决问题的能力［3］.

1 “数字信号处理”课程的特点

“数字信号处理”课程所涉及的内容广泛、理论复杂、概念抽象，造成很多学生在学习时甚感困难的现象，课程的具体特点如下［4］.

1）教学内容广泛，重点掌握难

该课程中时域离散信号与系统的频域分析这一章节的基本概念和基本理论，是学生学习和应用数字信号处理技术的基础性知识，它与前期“信号与系统”课程有着紧密的承接连贯性;该课程中离散傅里叶变换（DFT）和快速傅里叶变换（FFT）这两章的教学内容，属于该课程的重点知识，同时也是学生学习中的一个难点知识;该课程中无限脉冲响应数字滤波器的设计和有限脉冲响应数字滤波器的设计，实质上是关于前几章理论知识的一种综合性应用;该课程中信号的整数倍抽取与插值、数字信号处理中的量化效应等内容则需根据实际学时进行选学.

2）高等数学知识应用多，数学公式推导难

由于该课程中涉及复变函数、高等数学、信号与系统等理论知识.因此，学生学习数字信号处理技术，必然离不开数学公式的推导，如Z变换、序列的傅里叶变换（DTFT）、离散傅里叶变换（DFT）、傅里叶级数等概念及其性质，同时时域和频域抽样定理、利用DFT对信号进行频谱分析等内容，也都有大量的数学公式推导.而这些内容从本质上来讲，都属于是一种数学方法，并且这些数学计算也大都可以借助于计算机来完成.当然，大部分繁杂的数学公式推导并不需要学生掌握，只需要理解清楚相应结论即可.

3）基本概念抽象，物理含义理解难

该课程中涉及序列的傅里叶变换（DTFT）、Z变换、离散傅里叶变换（DFT）、快速傅里叶变换（FFT）等诸多变换，学生对其概念理解不清，很容易混淆.特别是学生对各种变换的物理含义理解不透彻，常感到无所适从，如DFT与Z变换及DTFT三者之间的关系、线性卷积与循环卷积之间的关系、DFT对连续时间傅里叶变换逼近过程的误差分析等内容.

2 加强Matlab的实践性教学

2.1 Matlab实践性教学的作用

Matlab（Matrix Laboratory，矩阵实验室）是由Math Works公司推出的一款数值计算和可视化型软件.它以较强的人机互动性和简单易学的程序语言，并借助简单的编程调试环境，现已成为信号处理领域中国际公认的仿真开发平台与标准软件［5］.

Matlab软件是以矩阵运算为基础，通过简单的函数调用，就可以方便地完成复杂的数字信号处理的相关运算，它在“数字信号处理”课程教学中的作用主要体现在以下三个方面.

1）在进行相关数学公式推导后，教师可以利用Matlab软件的编程直观生动地演示相应知识点的对应结果，有效地帮助学生理解和掌握数学公式所隐含的物理意义.

2）针对课程中的课后练习题，学生可以利用Matlab软件方便地完成以书面形式难以完成的作业，从而激发学生的学习积极性，提高学生的学习效率.

3）通过开设综合性或设计性实验，充分发挥学生动手实践的主动性与创造性，促进学生将所学知识学以致用，进而提高分析和解决实际问题的能力.

2.2 Matlab实践性教学的仿真实例

在“数字信号处理”课程教学过程中，将传统理论教学与Matlab软件的实践性教学结合起来，不仅可以增强课程教学内容的直观生动性，而且也可以使得学生能够真正理解数字信号处理领域中的基本概念，并掌握数字信号处理领域中的基本方法，同时还能激发学生的学习积极性，从而达到事半功倍的效果.为了验证该方法的有效性和可行性，该文以系统零极点的位置对系统频率响应的影响为仿真实例，对Matlab软件在“数字信号处理”课程中的应用加以探讨.

离散时间线性时不变系统函数的零极点对系统频率响应的影响是“数字信号处理”课程中的一个重要知识点，也是学习中的难点［6］.为了减少数学公式推导给学生带来的疑惑和困扰，使学生直观清晰地观察零极点对系统频率响应的影响，该文选择最简单的一阶离散系统，其系统函数为H（z）=，假设系统的零点q在原点，极点p分11别取 0.2，0.5，0.8，则此一阶离散系统极点的位置对幅频特性的影响如图1所示.

图1 一阶离散系统极点的位置对幅频特性的影响

由图1可见，这些一阶系统是滤波性能较差的低通滤波器.单位圆内越靠近单位圆的极点，对系统幅频特性凸峰的位置及峰值的影响越明显.如在ω→0处，p1=0.8时比 p1=0.2和 p1=0.5 时更靠近单位圆，因此幅频特性凸峰的峰值比其它两种情况明显.由此得到如下结论:系统的极点影响幅频特性的峰值，且极点越靠近单位圆，幅频特性对应的峰值越高.

对上述一阶离散系统，假设系统的极点p1在原点，零点 q1分别取 0.2，0.5，0.8，则此一阶离散系统零点的位置对幅频特性的影响如图2所示.

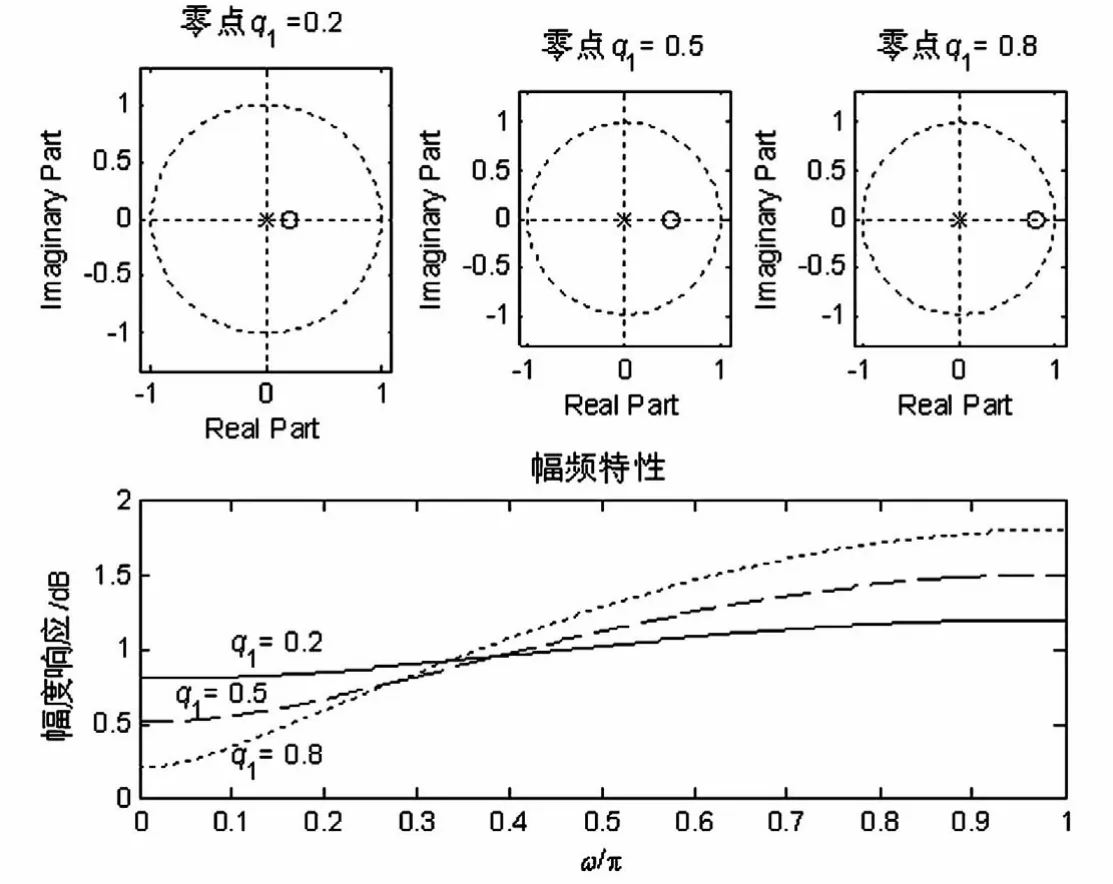
图2 一阶离散系统零点的位置对幅频特性的影响

由图2可见，这些一阶系统是滤波性能较差的高通滤波器.单位圆内越靠近单位圆的零点，对系统幅频特性凹谷的位置及谷值的影响越明显.如在ω→0处，q1=0.8时比 q1=0.2和 q1=0.5 时更靠近单位圆，因此幅频特性凹谷的谷值比其它两种情况明显.由此得到如下结论:系统的零点影响幅频特性的谷值，且零点越靠近单位圆，幅频特性对应的谷值越低.

综上所述，将Matlab仿真软件引入“数字信号处理”课程进行实践性教学的方法，使得系统零极点的位置对系统频率响应的影响这一知识点以形象直观的图形展示出来，有效地减少了相关的数学公式推导环节，在节约课堂时间的同时，一方面能让教师轻松突破难点，另一方面也能让学生明明白白、清清楚楚地掌握相应的知识内容，极大地提升了教学效果.

3 结语

“数字信号处理”既是一门理论性和实践性都很强的课程，又是一门让学生时感畏难的课程.为了有效地解决课程教学过程中出现的学生对知识点理解困难、学习枯燥无味、教学效果差等问题，该文针对“数字信号处理”课程的特点，采用了传统教学结合Matlab仿真软件加强实践性教学的方法.通过以系统零极点的位置对系统频率响应的影响为仿真实例，将抽象的概念、枯燥的公式、复杂的物理含义用图形直观生动地表示出来，使学生对“数字信号处理”课程的理论知识和分析设计方法有了更深入的理解.同时，Matlab仿真软件简单易学，有助于学生在有限的课堂时间内，将数学公式与物理含义有机结合，迅速掌握与数字信号处理技术相关的理论知识，从而实现数字信号处理知识的灵活运用.

［1］袁小平，王艳芬，史良.基于Matlab的《数字信号处理》课程的实验教学［J］.实验室研究与探索，2002，21（1）:58－60.

［2］曹建玲，朱联祥，刘焕淋.“数字信号处理”课程教学改革与实践［J］.中国电力教育，2011，（20）:75－76.

［3］曹昕燕.基于Matlab的数字信号处理课程改革［J］.长春大学学报，2007，17（2）:95－97.

［4］程佩青.数字信号处理教程［M］.第3版.北京:清华大学出版社，2007.

［5］方益明.提高“数字信号处理”课程教学效果的研究［J］.电气电子教学学报，2009，31（3）:15－16.

［6］高西全，丁玉美.数字信号处理［M］.第3版.西安:西安电子科技大学出版社，2008.