小天体着陆动力学参数不确定性影响分析
2014-03-06袁旭朱圣英乔栋崔平远
袁旭,朱圣英,乔栋,崔平远
(1.北京理工大学小天体探测与防御实验室,北京100081;2.飞行器动力学与控制教育部重点实验室,北京100081)
小天体着陆动力学参数不确定性影响分析
袁旭1,2,朱圣英1,2,乔栋1,2,崔平远1,2
(1.北京理工大学小天体探测与防御实验室,北京100081;2.飞行器动力学与控制教育部重点实验室,北京100081)
针对小天体不规则程度高、引力场复杂,且物理参数存在较高不确定性的问题,基于小天体着陆动力学方程线性化近似解析解,对各动力学参数不确定性的影响进行了分析。考虑动力学方程线性化带来的误差,引入线性化误差补偿校正方法,建立了探测器轨迹对动力学参数不确定性的敏感度方程。以小行星Eros 433为例,重点分析了目标小天体质量、自转角速度、引力势函数系数,以及探测器初始状态、推力加速度等动力学参数不确定性对探测器着陆轨迹的影响。数学仿真分析表明,针对本文选取的目标小天体,推力加速度扰动为主要影响因素,探测器初始状态的不确定性为次要影响因素,其他参数扰动的影响较小。
小天体;着陆;参数不确定性;敏感性分析
0 引言
对小天体的探测研究,有利于人们认识和研究太阳系的起源与演化。因此,小天体探测是21世纪深空探测活动的重要内容[12]。其中,着陆探测由于能够进行现场科学探测,因而引起学者的广泛兴趣[34]。迄今,各国的小天体探测任务中,有2次成功完成了着陆任务,分别为美国航空航天局(NASA)发射的NEAR探测器于2001年2月着陆于Eros 433小行星[5],和日本宇宙航空研究开发机构(JAXA)发射的Hayabusa探测器于2005年11月着陆于Itokawa小行星并采样返回[6]。此外,欧洲太空局(ESA)发射的Rosetta探测器预计将于2014年11月对Churyumov-Gerasimenko彗星进行着陆探测[7]。
形状的不规则性是小天体显著的物理特征。由于形状极度不规则,小天体引力场环境较为复杂,小天体的各物理参数也存在较大的不确定性[89]。这种参数不确定性会对小天体着陆过程产生影响,给小天体着陆任务带来挑战。同时,发动机推力误差等探测器自有误差也对小天体着陆精度造成影响。因此,有必要对小天体着陆过程中参数不确定性的影响进行分析与研究,通过分析各参数不确定性对探测器状态的影响程度,可重点关注影响较大的参数并设法减小相应的误差。Broschart等对小天体固联坐标系下探测器的平移与下降运动特点进行了大量研究,并进行了敏感性分析,取得了显著的研究成果[10]。
本文针对小天体下降与着陆过程,首先给出动力学方程并对其线性化,利用线性化方程对探测器状态及其他变量求解。基于这些方程和敏感性分析方法,研究了探测器状态对参数不确定性的敏感度,对相同条件下处于不同区域时探测器状态对各参数的敏感度进行了分析与比较,并以Eros 433小行星参数[9]为例给出了仿真分析结果。
1 系统动力学模型
1.1 坐标系
本文采用小天体固联坐标系Σb:原点ob位于小天体质心,zb轴与小天体最大惯量轴即自转轴重合,xb与yb轴分别与最小和中间惯量轴重合,xb, yb,zb三轴满足右手法则,如图1所示。

图1 小天体固联坐标系Fig.1 Small celestial body fixed frame
1.2 动力学方程
假设小天体密度均匀并绕其最大惯量主轴匀速转动,忽略其他干扰力,在小天体固联坐标系下,选取探测器位置、速度为状态变量,即

则探测器的动力学方程可表示为

其中,ω为小天体自转角速度;Tx,Ty,Tz为探测器控制力形成的三轴加速度分量;V为小天体引力势函数;为三轴的小天体引力加速度分量。
小天体引力势函数采用球谐函数形式,即

其中,Pnm为缔结勒让德多项式;Cnm和Snm为小天体引力场对应的球谐函数各阶系数;a为小天体名义半径;θ,φ,r分别为探测器所处的经度、纬度和半径,满足
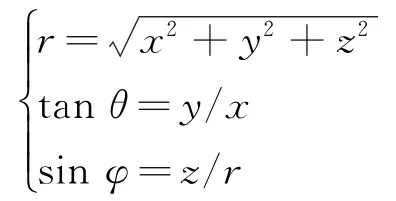
1.3 动力学方程线性化
由于探测器受到的小天体引力加速度与探测器位置有关,因此式(1)所示的动力学方程为非线性方程,且无法求出精确解析解。在一些情况下,需要解析形式的近似解。此时可将式(1)进行线性化处理,得到近似的线性化方程

其中
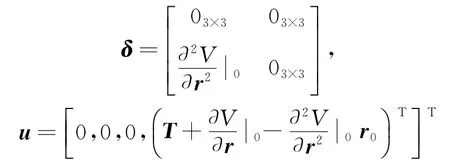
则可求出此线性方程的解析解

虽然探测器的运动存在很大的非线性,但线性化假设可在一定精度下简化分析过程,并能获得解析形式的近似解,便于进一步的分析,在初期的理论推导和任务设计阶段是非常方便和重要的分析手段。
由于矩阵A+δ可逆,若在研究的时间范围内,推力加速度T为常矢量,则此解可进一步化简为

式(5)即为常推力加速度下动力学方程式(3)的线性近似解析解。
2 线性化误差校正
2.1 利用线性化方程求解未知变量
式(5)中含有6个方程,包括始末状态、推力加速度、作用时间共计16个变量。若已知其中10个变量,则可求解出6个未知变量。
例如,若已知初始状态X(0),欲在常推力加速度T作用下经时间tf到达末端位置rf,则可求得T和到达末端位置时的速度vf分别为:

2.2 线性化误差及误差校正
线性化方程求解出的探测器状态为近似解,与真实状态存在误差。探测器的真实状态X*(t)可表示为
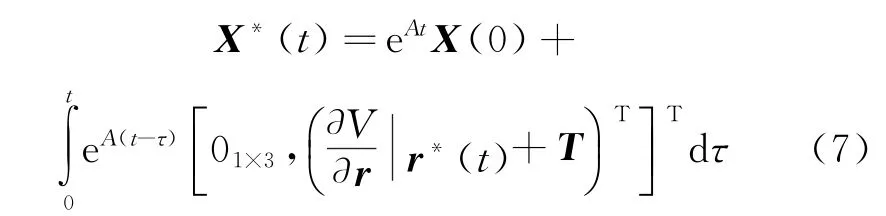
则线性化误差可表示为

假设在适当时间范围内,线性化解(5)的轨迹接近真实轨迹,且此区域内也很接近,则可认为在此区域内进行线性化带来的误差总是近似相等的。这样,可对式(6)所求得的推力加速度T进行校正[10]:按照非线性方程式(1)进行数值求解后,可求出末时刻的线性化误差E(tf)。基于X*(tf)附近不同轨迹对应的E(tf)近似相等的假设,可设一个用于校正的,满足
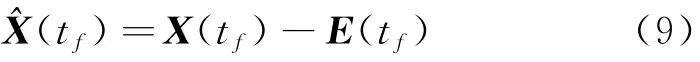
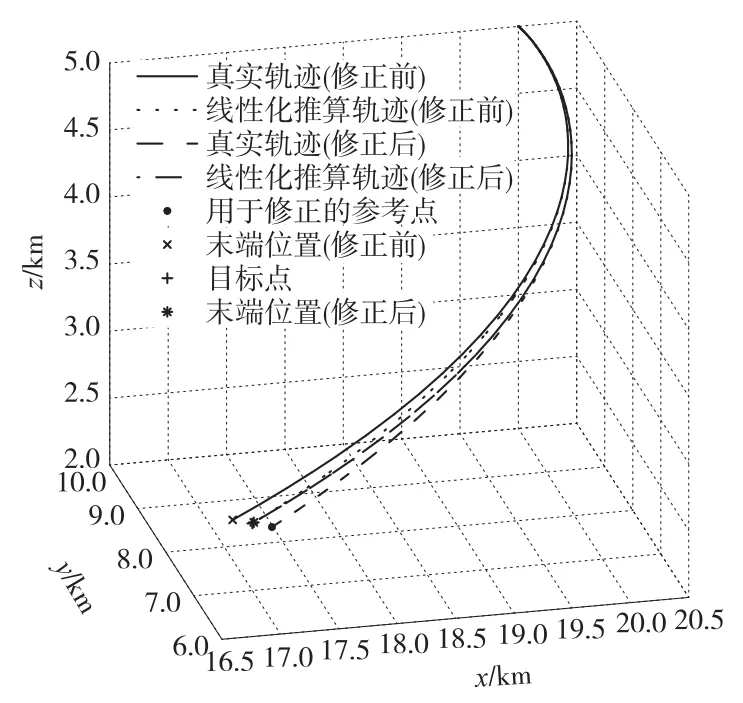
图2 线性化误差修正示意图Fig.2 Scheme of linearization error calibration

图3 线性化误差修正局部放大图Fig.3 Calibration scheme partially amplified
3 探测器状态对参数不确定性的敏感度
从动力学方程的解式(5)及引力势函数式(2)可以看出,探测器t时刻的状态变量X(t)与其初始状态、发动机推力加速度、小天体自转角速度、质量和球谐函数各阶系数有关,即

于是,式(10)中各参数的误差或不确定性都会对探测器的状态与着陆轨迹产生影响。
在tf时刻,以αi,i=1,2,...,k表示参数ω, M,Cnm,Snm,X(0),T,则X(tf)的协方差矩阵可表示为:
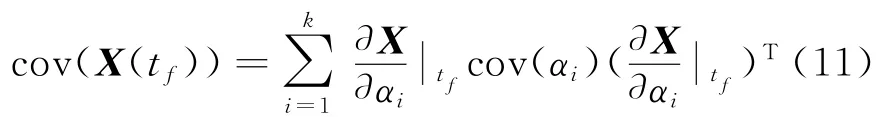
由式(11)可以看出,X(tf)的不确定度与各参数的不确定度和X(tf)对该参数的敏感度矩阵有关,即由系统状态方程和各参数不确定度共同决定。探测器状态对某参数的敏感度矩阵可由以下过程求得[11]
结合动力学方程
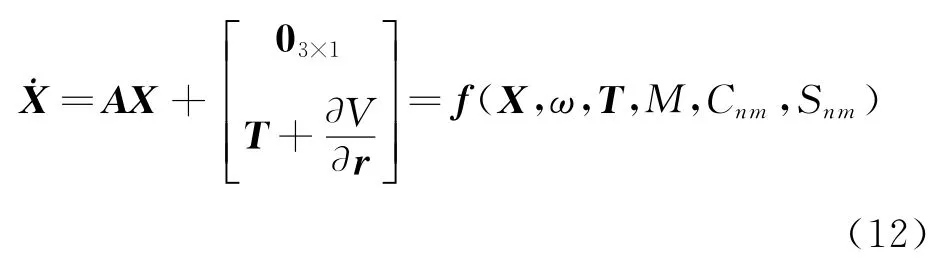
对某一参数αi,其敏感度矩阵满足
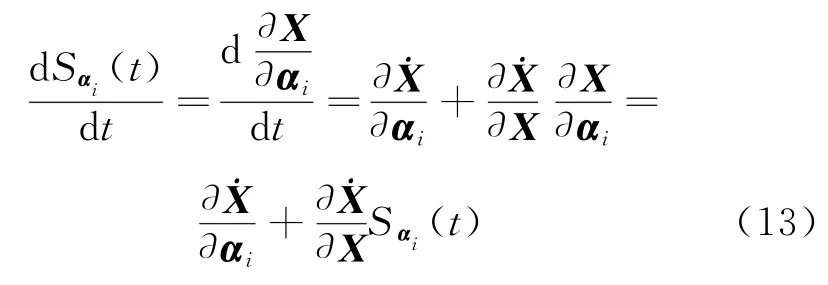
通过解上式中的微分方程即可求出对某参数的敏感度矩阵,再结合该参数的不确定度,即可得到某时刻探测器状态X(tf)的不确定度。
由式(11)可见,已知各参数不确定的情况下,探测器状态对各参数的敏感度矩阵随时间变化,因此由某一参数扰动引起的探测器状态不确定度也随时间变化。可研究相同条件下,同一时刻各参数不确定性对探测器状态的影响,来比较某一任务中不同参数扰动的作用大小;对某一参数,可研究探测器处于不同区域(初始状态)时,其状态受该参数扰动影响的差异。这里,取探测器位置向量协方差阵最大特征值的平方根作为探测器位置不确定度的度量指标
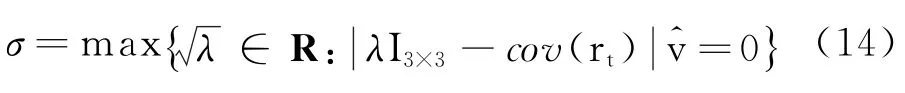
4 仿真与分析
4.1 线性化误差校正的仿真分析
以Eros 433小行星为例进行仿真分析。假设探测器在常推力作用下沿径向向小行星表面下降(即保持经纬度不变)。仿真中选取探测器初始位置半径为20 km,经纬度选取多组数据以比较,初始速度大小为3.0 m/s,方向指向小天体质心即坐标系原点,末端位置半径为17.8 km,运动时间为1 000 s。在某一初始位置,可由式(6)计算所需推力加速度并通过式(9)校正。仿真末端位置与目标末端位置的偏差(距离)随初始位置的经纬度不同而变化,可绘制等高线图表示。仿真所用参数参照NEAR任务获得的数据,如表1所示,未经误差校正和校正后末端位置偏差的区域分布如图4和图5所示。

表1 仿真参数Table 1 Simulation parameters
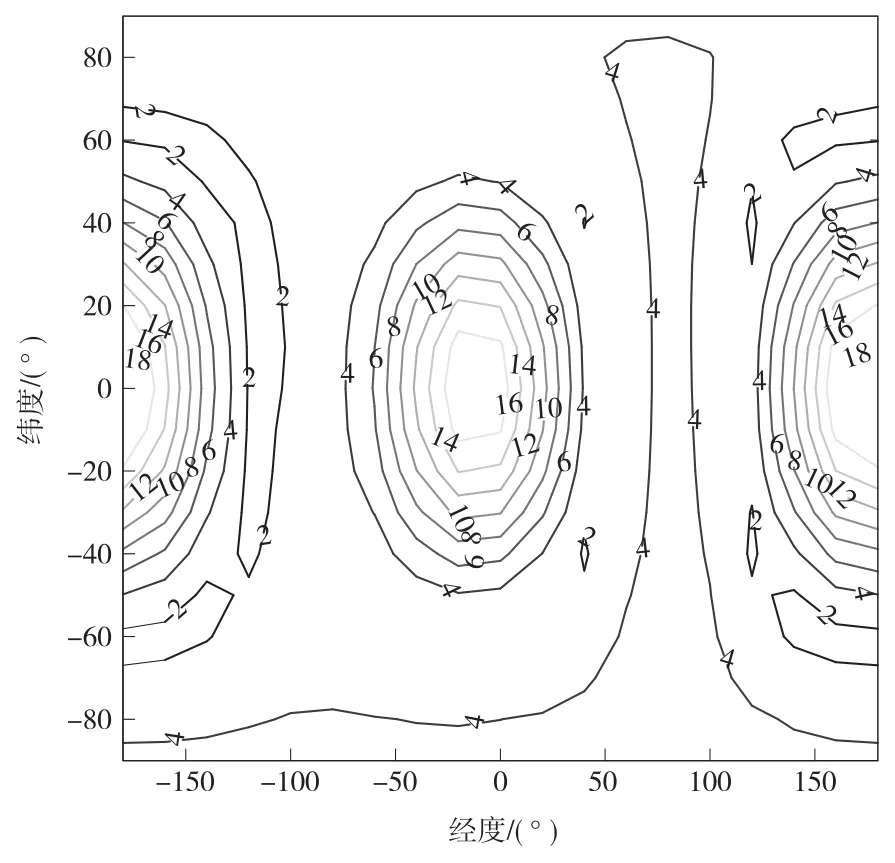
图4 未校正时末端位置与目标位置偏差等高线图(单位:m)Fig.4 Contour map of terminal position offset from target without calibration(unit:m)
由图4和图5可见,在此仿真条件下:
1)校正前的末端位置偏差一般处于米级,校正后减小至厘米级,精度提高了2个数量级,表明此校正方法非常有效。

图5 校正后末端位置与目标位置偏差等高线图(单位:cm)Fig.5 Contour map of terminal position offset from target after calibration(unit:cm)
2)纬度愈靠近0°,经度愈靠近0°或±180°,即愈靠近xb轴,则偏差愈大。这表明愈靠近长轴,小天体形状的不规则度愈大,引力加速度的非线性愈强,线性化引入的误差愈大。
4.2 探测器状态对参数敏感度的仿真分析
仿真参数仍如表1所示,各参数的1—σ不确定度参照NEAR任务中获得的数据以及文献[10],如表2所示。

表2 仿真参数的1-σ不确定度Table 2 1-σuncertainty of the simulation parameters
其中,对球谐函数系数的不确定度考察到3阶, Tmag,ϕT,θT分别代表推力加速度大小和推力方向角。
探测器末端位置不确定度以式(14)中σ表达,得到图6所示的等高线图。由各参数扰动引起的不确定度数量级如表3所示,其中推力加速度扰动引起的末端位置不确定度分布如图7所示。
在此仿真条件下:
1)将图6与图7进行比较发现,二者等高线图非常相似,数值也非常接近,表明末端位置的不确定度主要源于推力加速度的不确定性,即末端位置不确定度受发动机推力不确定性影响最大,发动机推力偏差是影响探测器着陆轨迹不确定度的主要因素。

表3 各参数扰动引起的末端位置不确定度的数量级Table 3 Order of magnitude of terminal position uncertainty due to uncertainty of each parameter alone

图6 末端位置不确定度等高线图(单位:m)Fig.6 Contour map of terminal position uncertainty(unit:m)

图7 参数T扰动引起的末端位置不确定度等高线图(单位:m)Fig.7 Contour map of terminal position uncertainty due to uncertainty of T(unit:m)
2)末端位置的不确定度为10 m级,主要分布于30~50 m范围。推力加速度偏差引起的末端位置不确定度为10 m级,主要分布于25~45 m范围,为主要影响因素;初始状态偏差引起的末端位置不确定度为米级,主要分布于5~6 m范围,为次要影响因素;小天体质量、引力势函数系数、自转角速度不确定性引起的末端位置不确定度均小于米级。可见在此仿真条件下,探测器轨迹的不确定度主要受推力偏差影响,其次受初始状态误差影响,受其他参数扰动的影响较小。
5 结论
本文对小天体着陆过程中探测器状态对小天体及探测器参数的敏感性进行了简要的分析。首先,建立非线性动力学方程并进行了线性化,得出线性化方程的近似解析解。基于线性化方程,得出常推力下求解未知变量的方法,并引入一种线性化误差校正方法。探测器状态的不确定度由各参数不确定度和探测器状态对各参数的敏感度共同决定。通过敏感性分析,比较了探测器着陆轨迹在相同条件下受各参数扰动影响的区别和处于不同区域时受某一参数扰动影响的差异。在本文的仿真条件下,推力加速度的扰动为主要影响因素,初始状态的不确定性为次要影响因素,其他参数扰动的影响较小。
[1] 崔平远,乔栋.小天体附近轨道动力学与控制研究现状与展望[J].力学进展,2013,43(5):526- 539.[Cui P Y,Qiao D. Research progress and prospect of orbital dynamics and control near small bodies[J].Advances in Mechanics,2013, 43(5):526- 539.]
[2] Furfaro R,Cersosimo D,Wibben D R.Asteroid precision landing via multiple sliding surfaces guidance techniques[J]. Journal of Guidance,Control,and Dynamics,2013:1-18.
[3] Barucci M,Cheng A F,Michel P,et al.MarcoPolo-R nearearth asteroid sample return mission[J].Experimental Astronomy,2012,33(2- 3):645- 684.
[4] Michel P,Barucci M A,Cheng A F,et al.MarcoPolo-R: near-earth asteroid sample return mission selected for the assessment study phase of the ESA program cosmic vision [J].Acta Astronautica,2014,93(0):530- 538.
[5] Dunham D W,Farquhar R W,Mcadams J V,et al. Implementation of the first asteroid landing[J].Icarus, 2002,159(2):433- 438.
[6] Uo M,Shirakawa K,Hashimoto T,et al.Hayabusa's touching-down to Itokawa-autonomous guidance and navigation[J].The Journal of Space Technology and Science, 2006,22(1):41.
[7] Ulamec S,Biele J,Bousquet P,et al.Landing on small bodies:from the Rosetta lander to{MASCOT}and beyond [J].Acta Astronautica,2014,93(0):460- 466.
[8] 崔平远,朱圣英,崔祜涛.小天体自主软着陆脉冲机动控制方法研究[J].宇航学报,2008,29(2):511- 516.[Cui P Y,Zhu S H,Cui H T.Autonomous impulse maneuver control method for soft landing on small bodies[J].Journal of Astronautics,2008,29(2):511- 516.]
[9] Miller J K,Konopliv A S,Antreasian P G,et al. Determination of shape,gravity,and rotational state of asteroid 433 Eros[J].Icarus,2002,155(1):3- 17.
[10] Broschart S B,Scheeres D J.Spacecraft descent and translation in the small-body fixed frame[C]//Proc.AIAA/ AAS Astrodynamics Specialists Meeting.Providence,RI, USA:[s.n.],2004.
[11] Montenbruck O,Gill E.Satellite orbits:models,methods, and applications[M].Berlin Heidelberg:Springer,2000.
电话:(010)68918910
E-mail:yuanxu1020@126.com
[责任编辑:宋宏]
Impact Analysis of Dynamic Parameters Uncertainty on Small Celestial Body Landing
YUAN Xu1,2,ZHU Shengying1,2,QIAO Dong1,2,CUI Pingyuan1,2
(1.Laboratory of Asteroid Exploration and Defense,Beijing Institute of Technology,Beijing 100081,China;2.Key Laboratory of Dynamics and Control of Flight Vehicle,Ministry of Education,Beijing 100081,China)
To the challenge of high degree irregularity,complex gravity field and relatively high degree of physical parameters uncertainty of small celestial bodies,the impact of dynamic parameters uncertainty is analyzed, based on the approximate linearized analytical solution of the small celestial body landing dynamic equations.A calibrating method is used to compensate the errors brought in by linearization.And the sensitivity equations of spacecraft trajectories to dynamic parameters are established.Taking the asteroid Eros 433 as an example,the impact of the uncertainty of the mass,rotation rate and gravitational potential coefficients of the target body on the spacecraft landing trajectory,the initial state of the spacecraft and the thrust acceleration are analyzed elaborately. Mathematical simulation shows that for this selected target body,the thrust acceleration disturbance is the primary factor of such impact,and the initial state of the spacecraft the secondary one.And the impact of other parameters are relatively small.
small celestial body;landing;parameters uncertainty;sensitivity analysis
V448.21
:A
:2095-7777(2014)02-0134-06
袁旭(1986—),男,博士研究生,主要研究方向:深空探测器自主导航与控制
2013-11-01
2013-12-30
国家重点基础研究发展计划(973计划)(2012CB720000);国家自然科学基金(61304248);基础科研计划(B2220110012);民用航天预先研究计划
