基于地表有效保水量的森林火险天气等级预报1)

2014-03-06王艳霞周汝良

东北林业大学学报 2014年3期

王艳霞周汝良丁琨

(西南林业大学，昆明，650224)

森林火险天气等级预报，主要根据能反应天气干湿程度的气象因子来预报天气条件能否引起森林火灾的可能性。这种林火预报对实现有针对性的排兵布阵、扑救资源调度、火源检查与巡护、火情监测与瞭望等，对全社会涉林人员杜绝林区火源、警惕并预防林火发生，都具有十分重要的现实意义［1］。作为影响森林火灾的主要因素之一，降水可增加可燃物的含水量从而降低火险系数，是各国火险天气等级预报的必要因子［2］。因此，较为准确地描述地表实际水分状态，特别是复杂多变的山地区域，对进一步提高中长期火险天气等级预报的准确性和可靠性具有重要作用。

《全国森林火险天气等级》根据最高空气温度、最小相对湿度、前期或当日的降水量及其后的连续无降水日数、最大风力等级、物候等因子预报森林火险天气等级。现有标准以每日为时间单位进行短期火险天气等级预报。当森林防火工作需中长期(如以旬、月为时间单位)火险天气等级预报时，气温、湿度、风力、物候等预报因子可根据气象站(台)观测的资料获取，而降水量及其连旱天数所代表的降水火险指标，难以直接用于森林火险的预报工作。一方面，现有标准认为降水过后如果连续无降水日数越多，火灾发生的危险性越大，这种方式难以表达出一段时间内的可燃物水分散失情况，从而不适合开展中长期森林火险天气等级预报。另一方面，现有国家标准指数计算的本质是分段函数模型，存在严重的阶跃问题，往往微小差异数据计算出来的火险等级差异较大，存在较大的预报误差。

目前，许多研究者提出了森林火险天气等级预报的方法，但针对中长期火险天气等级预报的文献较少见。张学艺［3］参考国内外火险天气等级预报方法研究的思路及森林火险等级划分标准，针对宁夏的实际情况，对指标体系进行逐月调整，运用多个气象因子和综合因子之间相关关系，来确定森林火险天气等级标准。冯家沛等［4］通过对连云港市1987—1993年大小不同的111 次林火查找原因并进行天气分析，指出原全国森林火险天气等级方法的不合理部分，并加以改进，增加了实效雨量、积雪深度等预报因子。高仲亮［5］选取1950—2010年云南省各地州的降水量、平均相对湿度、蒸发量、温度和风速数据，建立了蒸发量的线性回归模型，计算降水量和蒸发量之间的差值作为有效保水量，预报云南森林火险天气等级。王艳霞等［6－9］使用1950—1980年云南气象观测数据，采用高桥公式计算了蒸发量，通过累积求和计算有效保水量，提出了预报云南森林火险等级方法。以上预报方法，对行业标准中的不准确问题做了改进，但改进模型的普遍适应性、可行性存在一定不足或不全面。例如:降水在下垫面作用下的径流分配与土壤渗透、无积雪区域预报、降水在连续干旱条件下的蒸发与再吸水、经验统计回归模型的跨区域实用性、预报因子的计算精度等问题，都有待进一步研究解决。

1 研究区概况

云南地处中国西南边陲，位于北纬21°8'32″ ～29°15'8″，东经97°31'39″ ～106°11'47″，东西横跨864.9 km，南北纵距990 km，总面积3.94 ×105km2。北回归线横贯云南省南部，其山地区域地形复杂，高差起伏大，山地微气候特征突出。“十里不同天、一山分四季”，是云南山地微气候时空分布格局的真实写照。同时，由于云南干湿季分明，冬春季节几乎无降水，造成了森林火灾高发、频发的自然格局。云南山地地形复杂多样，森林可燃物类型多样，载量变化快，山区林农交错分布，火源多而复杂。

2 研究方法

2.1 数据收集

收集云南119 个常规气象站1993—2007年的观测数据，主要包括1—12月月均降水量、温度、湿度等指标。收集山地环境梯度数据，主要有:高程数据(DEM)、纬度、坡度、坡向、沟谷指数、纬度、坡向指数等。

研究区地形及山地微气候复杂，气象观测站稀少，分布不均匀。为了尽可能反映山区地形对气象要素分布的影响，本研究使用1∶ 250 000 比例尺的DEM，其数据空间分辨率重采样为100 m。利用地理信息系统中的空间模拟方法(如关联函数法、克里金法)对温度、湿度、风速等气象因子进行空间连续化模拟，收集除降水火险因子之外的其他因子的空间分布数据。

2.2 模型的建立

陆面蒸发量的计算:由于蒸发量观测的准确资料很少，蒸发量的计算依赖于间接计算。根据谭冠日等［10］的检验，认为傅抱璞［11］蒸发量计算公式误差较小，且公式较严密，具有普遍意义，傅抱璞根据水热平衡原理提出的陆面蒸发量计算公式为:

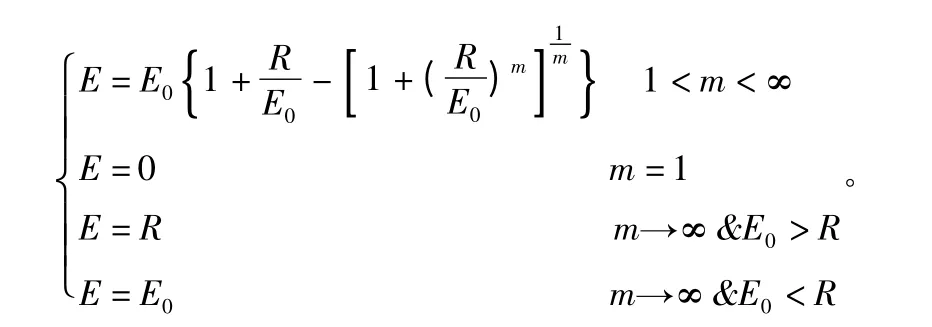
式中:E 为陆面蒸发量;E0为蒸发力;R 为降水量;m为下垫面参数。

使用对高桥公式进行修正并增加了海拔高度订正项后E0模型［10］:

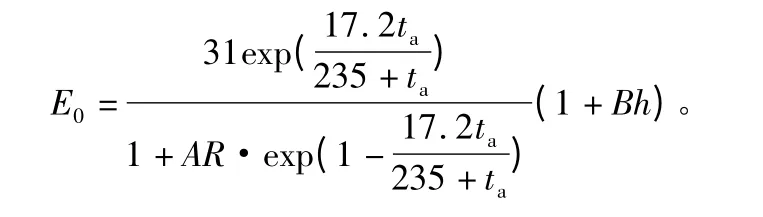
式中:ta为温度;R 为降水量;h 为海拔;A、B 为订正系数，A=1.2 ×10－3，B=8 ×10－5。

下垫面参数的空间模拟:地表径流越大，森林土壤的含水率越少，降水对降低火险的作用越小。傅抱璞［11］认为下垫面的透水性好坏决定了地表植被、地表径流的情况，故将下垫面参数(m)引入到陆面蒸发计算模型中。当m 取极小值1 时，表示下垫面透水性最差，植被最少，地面坡度最大，地表径流最强，陆面蒸发为0，即降水量全部以地表径流形式流走，未参加地面蒸发过程。反之，下垫面透水性好，其覆盖的植被多，地形平坦，地面径流就小，m 值就越大，表示全部降水都参加了地面蒸发过程。

谭冠日等［10］以云南为研究对象，指出下垫面参数与地形起伏度有较好的关系，提出了m 的计算公式:

其中:m 为下垫面参数;U 为地形起伏度;Ct为研究区域经纬线与等高线的交点总数;Lm为经纬线总长度;ΔH 为等高线间距;Km为地图比例尺。

利用ArcInfo 的栅格运算功能，采用DEM 的窗口分析法，在GRID 模块下基于DEM 提取地形起伏度，其计算理论为一定区域内最大高程和最小高程的差［12］，即:U =Hmax－Hmin。其中，Hmax为分析窗口中的最大高程值;Hmin为分析窗口中的最小高程值。用1∶ 250 000 的DEM 作地形起伏度计算时，最佳分析窗口取21 ×21 大小［13］。

地表有效保水量计算模型:将地表有效保水量估算为地表降水量与同时期陆面蒸发量差值的动态累加值，即:Rx=其中，Rx为地表有效保水量;Ri为降水量;Ei为陆面蒸发量。

云南11月至次年4月为旱季，在此期间，地面蒸发量很大，在当年的雨季所保有的水分大部分在旱季结束前蒸发。本研究视旱季结束，雨季到来之前，即前一年4月结束时，森林火灾常发地区的地表有效保水量达最小值，从5月份开始，以0 值开始重新计算地表有效保有水分。

地表有效降水火险天气指标模型的建立:由于森林火险指数的确定主观因素比较大，没有客观定量的评述标准，因此将降水火险指标按照［0，50］的取值范围，按研究区多年月平均保水量的总体情况，定义有效保水量(Rx)的区间取值，根据经验确定其打分值，得到森林火险天气指数(F)，结果如表1所示。

表1 有效保水量对应的森林火险天气指数打分表

采用表1地表有效保水量各区间的中间值和其对应森林火险指数建立样本点集合:{(117，45)，(243，40)，(369，35)，(495，30)，(621，25)，(687，20)}。由于火险有最高和最低限制，本研究采用S形曲线形状的Logistic 生长曲线模型［14］(函数形式为:Y=(1/u+b0bx1)－1，其中u 为上限值)，则u =50。将表1所反映的分段打分函数改为连续函数形式，得到有效保水量的森林火险天气指数计算模型:F=50/(1 +50 ×0.002 ×1.004Rx)。其中，F 为有效保水量的森林火险指数;Rx为地表有效保水量。

气象因子的空间连续化模拟:预报因子的空间连续化是实现森林火险天气等级预报精细化的重要步骤。周汝良等［15］提出“对于许多宏观生态学、气象学、地表过程中一些物理指标的连续化模拟，如果只有少量稀疏样本数据，关联函数法应该是最好的内插方法”。因此，基于前人研究基础，使用关联函数法，对降水量、温度、湿度、风速等预报因子进行空间模拟，通用函数表达式如下:y =β0+β1x1+… +βpxp+ε 其中，y 为因变量，指降水量、温度、湿度等气象因子;x1、x2…xp为自变量，指海拔、经度、纬度等地理要素;p 为自变量的个数;β0为常数，β1、β2…βp为系数;ε 为误差。

3 结果与分析

3.1 降水量空间模拟

使用SPSS 软件，将气象站点观测的降水量数据及其环境梯度因子数据构成的样本集，使用逐步回归方法建立降水量关联函数内插模型，以4月月均降水量为例，公式为:R =1692.276－58.729A +2.342Cuv+9.896Slp。其中:R 为降水量(单位:0.1 mm);A 为纬度;Cuv为沟谷指数;Slp为坡度。该方程和系数均通过显著性和有效性检验。将纬度、沟谷指数、坡度栅格数据代入上述模型，使用ArcGIS 软件的栅格计算功能，计算得出连续化的降水量空间分布，如图1所示。

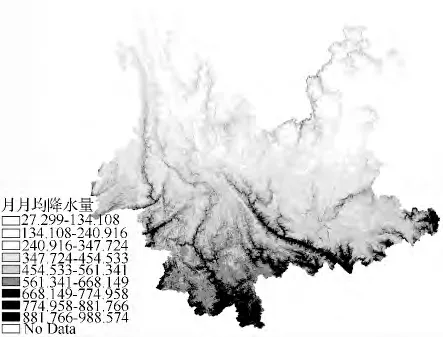
图1 连续化降水量空间分布图

3.2 地表有效保水量计算

下垫面参数空间模拟:云南省下垫面参数结果如图2所示，滇西、滇北的地形坡度大，下垫面透水性差，地表径流强，下垫面参数小，集中在1.1 ～2.5的范围内。滇东地形比滇西北平坦，植被覆盖多，下垫面透水性较好，m 值大，集中在3 以上。特别地区的m 值在图中显示为NODATA，表示U 值为0，m 值为无穷大，这表明地形平坦的地方，地表径流影响很小。

图2 云南省下垫面参数分布图

蒸发量计算:当下垫面参数m 为无穷大，在蒸发力空间分布(如图3)上以NODATA 值显示时，表明降水参加地表径流的部分很少，可视为没有。这种情况下，如果这些区域蒸发力值E0大于降水量R，则E=R;如果这些区域的蒸发力E0小于等于降水量R 时，则E=E0。

在旱季时，即使降水为0 时，云南省陆面蒸发量能达到5 ～15 mm。因此本文在计算蒸发量时若遇到降水量为零或计算的蒸发量不足15 mm 的月份时，默认此月的蒸发量为15 mm。将降水量、下垫面参数、蒸发力代入蒸发量计算的模型得到蒸发量的空间连续化分布图，如图4所示。从图中可以看出，纬度愈低，气温愈高，蒸发能力越强，蒸发量也就越大。总体上滇北温度、降水低于滇南，蒸发力小于滇南，其蒸发量也相对小。

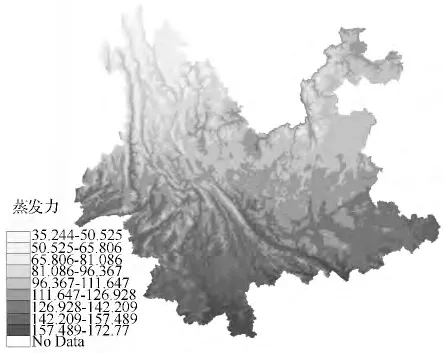
图3 蒸发力分布示意图

图4 蒸发量分布示意图

地表有效保水量计算:从图5看出，某些地方保水量值为负值，仅仅表示截止4月份的蒸发量值大于降水量，该地区比较干旱。当雨季到来，大规模的降水便会为这些地区补充水分。另外，林内植物夜间反吸水作用也缓解了蒸发对干旱的贡献。保水量为负值的地区的天气条件与保水量为正值的地区比较起来，干旱较严重，火险等级指数较高。从图中可以看出，保水量分布总体上南部多北部少，西部多东部少，这与云南旱季降水量分布趋势大体一致。

3.3 基于地表有效保水量的森林火险天气等级预报

云南4月月均保水量火险天气指数，见图6。从图中可以看出，该火险天气指数呈现空间连续变化的特点，不存在因一个县只有一个气象站点而出现的整个县域只有一个火险天气指数值的情况。火险天气指数较好的反映了云南历年因降水而表现出的森林火灾风险程度。全区域分东西两大阶梯变化，滇东大部分地区具有较大的火险天气指数，但具有大河谷存在的落雪和玉溪东南部地区火险天气指数相对较小;滇西北、哀牢山以西的滇西和滇南火险天气指数相对较小，红河干热河谷地带具有明显较高的火险天气指数，呈条带状沿元江、红河从滇中延伸至滇东南。

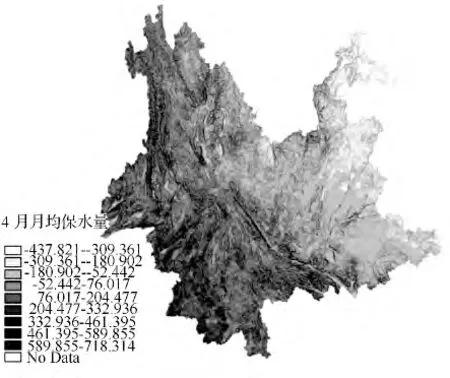
图5 有效保水量分布示意图

图6 地表有效保水量对应的火险天气指数图

根据云南省中长期火险天气等级预报模型，计算得出云南省历年4月月均森林火险天气等级(图7)。比较现有以行政区划为单位的火险天气等级预报(图8)，本文的预报结果因地理环境的不同而表现出连续变化的火险等级，从图7可以看出，火险等级呈逐级过渡，不存在相邻地区跨越2 级的地方。云南省4月份月均森林火险等级均较高，没有火险天气等级是1 级、2 级的区域，省内大部分地区为5级火险，火灾发生的危险性很高。滇北火险天气等级较滇南高，河谷火险天气等级却比周围地区高。各大河流域内火险等级相对低，但也在3 级到4 级，火灾较易发生。

图7 云南省4月份火险天气等级预报图

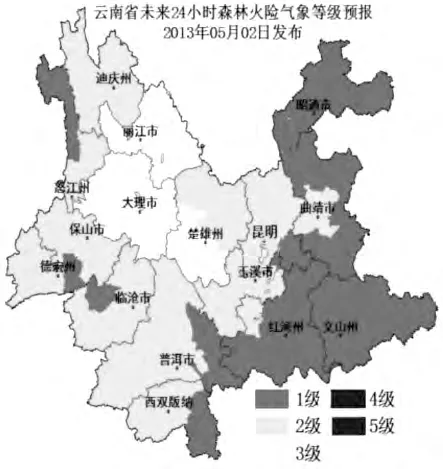
图8 以行政区划为单位的森林火险天气等级预报图

4 讨论与结论

在考虑地表径流的陆面蒸发量的基础上，探讨了云南地表有效保水量的机理模型，提出了使用表征干旱程度的地表有效保水量，衡量地表水分对森林可燃物的影响。进而建立了基于地表有效保水量的长期森林火险天气指数的连续化模型，并以栅格像素大小为单元预报了森林火险天气等级。

使用地表有效保水量代替降水量和连旱天数，充分考虑火险期内，连续时间上的地表降水的补充与蒸发消耗，建立的森林火险天气等级预报，弥补了现有国家标准的不足，具有较强的可推广性。与现有的国家森林火险天气等级预报标准、云南省及其他省份关于森林火险天气等级预报的改进方法［16－19］相比，本文所提出的地表有效保水量模型和连续化的火险天气指数模型，输入因子容易获取，方便建立计算机可实现的算法，结合GIS 的空间分析、地学统计分析、空间数据表达等功能，将预报因子空间连续化，可得到连续化分布的火险天气等级精细化预报图。预报结果能够预报出行政单位内部微地理区域上的火险情况，适用于山地起伏变化、气候变化异常的地理区域。

改进国家火险天气等级预报标准中的地表水分火险指数计算方法，将分段函数改进为连续曲线函数，克服了原有指标存在的阶跃性问题。连续化的火险指数模型更加符合火灾发生规律。

以1∶ 250 000 比例尺的DEM 和稀疏观测站点所测得的气象数据为基础，数据的精度存在进一步提高的空间。由于计算保水量的关键模型——陆面蒸发量计算模型，是传统较成熟的机理模型，且获取一年内有效保水量的实测数据较为困难，因此，未对蒸发量和保水量进行定量的真实性检验。如何结合热红外卫星影像反演地表温度、地表湿度等技术方法，缩短预报期限，进一步提高火险天气预报的实时性、准确性是后续研究的方向。

［1］舒立福，田晓瑞，寇晓军.林火研究综述(I):研究热点与进展［J］.世界林业研究，2003，16(3):37－40.

［2］林其钊，舒立福.林火概论［M］.合肥:中国科学技术大学出版社，2003.

［3］张学艺，李凤霞.宁夏森林火险天气等级预报方法的研究［J］.森林防火，2006(2):28－30.

［4］冯家沛，刘步宽.火险天气等级预报方法的研究［J］.森林防火，1998(1):37－39.

［5］高仲亮，周汝良，龙腾腾，等.基于蒸发量模型的云南省中期火险趋势分析与应用［J］.热带农业工程，2012，36(5):21－25.

［6］王艳霞，周汝良，何强.云南省森林火险等级预报系统［J］.山东林业科技，2007(3):13－15.

［7］易浩若，纪平，覃先林.全国森林火险预报系统的研究与运行［J］.林业科学，2004，40(3):203－207.

［8］杨崇军.森林火险天气等级预报与应用［J］.森林工程，2005，21(2):6－7.

［9］周明昆，王永平，高月忠.大理州森林火险天气预报方法［J］.江苏林业科技，2012，39(6):15－18.

［10］谭冠日，严济远，朱瑞兆.应用气候［M］.上海:上海科学技术出版社，1985.

［11］傅抱璞.山地蒸发的计算［J］.气象科学，1996，16(4):328－334.

［12］汤国安，刘学军，闵国年.数字高程模型及地学分析的原理与方法［M］.北京:科学出版社，2005.