林木联合采育机作业过程中的稳定性1)

苏永涛 刘晋浩 丁小康

(北京林业大学，北京，100083)

“十一五”国家科技支撑计划重大项目“多功能林木采育作业关键技术装备研究与开发”(2006BAD11A15)，研制成功了国内首台多功能林木采育装备。该多功能林木联合采育机，是集采伐、打枝、造材、集材、归堆、清林和采伐剩余物收集等于一体的机械，其提高了劳动生产率和木材生产的安全性，并改善了林区作业条件［1－3］。本文主要通过建立大脑情感学习模型，对获取的环境与运动数据信息进行融合，对多车辆稳定性作出判断;通过对联合采育机的纵向稳定性和横向稳定性两个方面进行研究［4］，为驾驶员提供危险预警，便于驾驶员的作业操作。

1 采育机纵向稳定性计算与判断

采育机作业稳定性，是指作业时不发生倾翻的能力。在作业过程中，由于坡度、方位角等一系列因素的影响，可能发生向前或向后的纵向失稳［5］。通过计算特征面外法矢量特征值，即可判断采育机向前或向后的静态稳定性:当外法矢量Z 值大于0时，即为该方向上的稳定状态;当外法矢量Z 值等于0 时，即采育机为该方向的翻倾临界状态;当外法矢量Z 值小于0 时，即采育机在该方向上为翻倾状态，采育机将会发生相应方向上的纵向失稳。

下面以向前的纵向失稳为例，分析计算采育机向前纵向失稳的计算与判断方法。

1.1 纵向稳定性计算

设平面MON 外法矢量为(XMON，YMON，ZMON)，分别计算平面MON 的内外法向量为:

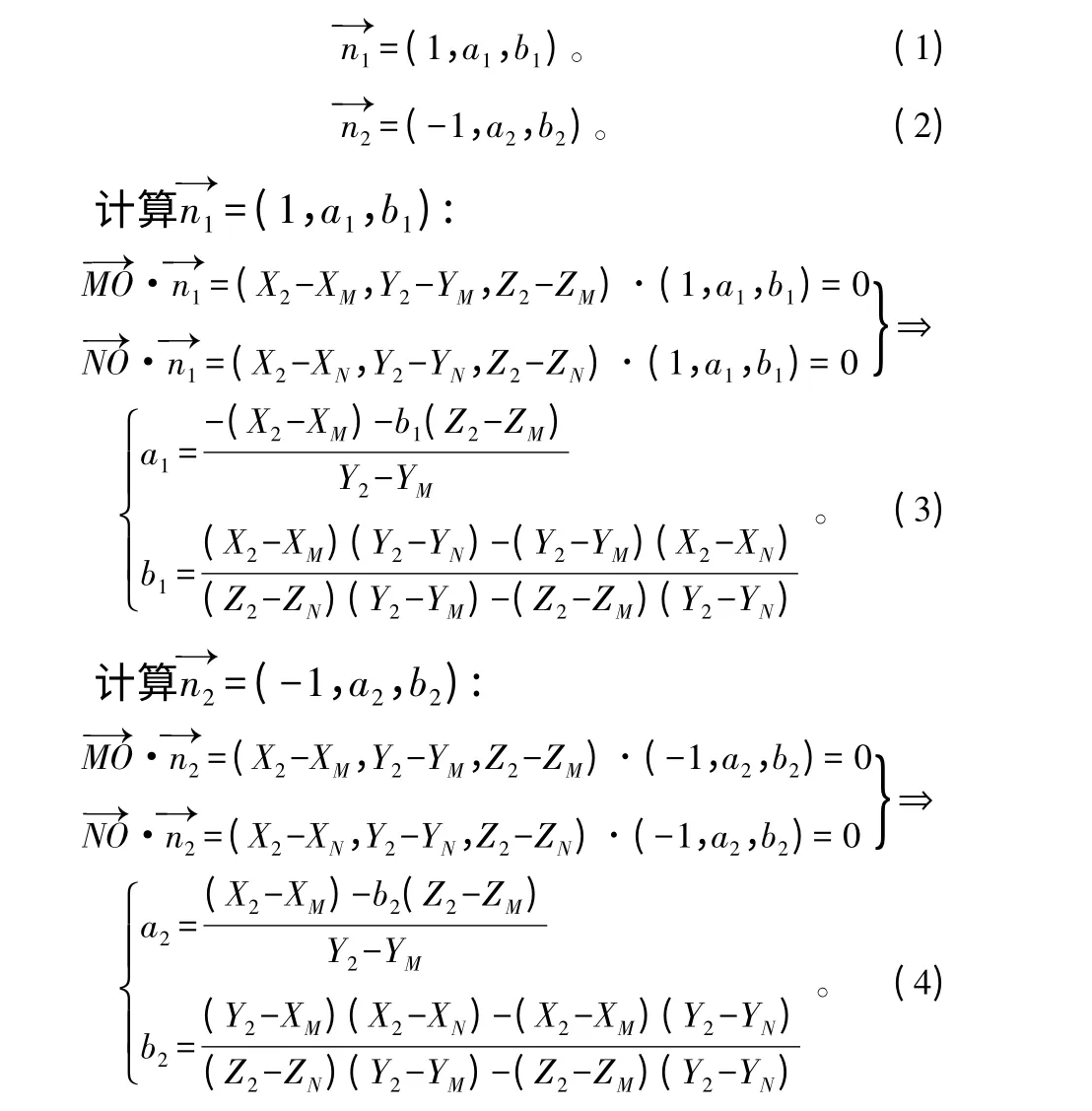
利用立体三角形中向量之间的夹角关系，判断平面MON 的外法矢量，并将相应的值赋给平面MON 的外法矢量(XMON，YMON，ZMON)。

1.2 纵向稳定性判断

根据特征矢量法，判断采育机向前稳定性。若ZMON＞0，则采育机向前为稳定状态;若ZMON=0，则采育机向前为倾翻临界状态;若ZMON＜0，则采育机向前为不稳定状态，向前翻倾。

利用相同计算方法，可计算并判断采育机向后的稳定性。设平面POQ 外法矢量为(XPOQ，YPOQ，ZPOQ)，则:若ZPOQ＞0，则向后为稳定状态;若ZPOQ=0，则向后为倾翻临界状态;若ZPOQ＜0，则向后为不稳定状态。

2 采育机横向稳定性计算与判断

2.1 横向一级稳定性计算与判断

采育机在作业过程中，除了可能发生前后的纵向失稳外，还会发生横向的失稳。由于采育机后桥与整机的链接只有一个支撑点，因此，后桥可以产生上下自由摆动，后桥与前轮接地点连线构成了采育机横向一级失稳的翻倾轴;所以，在计算采育机横向一级失稳的过程中，应采用的质心为整机除后桥外的质心用于计算。通过计算翻倾轴与整机除后桥外质心构成平面的外法矢量，即可判断采育机横向一级失稳向左或向右的静态稳定性。当外法矢量Z＞0时，即为该方向上的稳定状态;当外法矢量Z=0 时，即采育机为该方向的翻倾临界状态;当外法矢量Z＜0 时，即采育机在该方向上为翻倾状态，其将会发生相应方向上的横向一级失稳。

下面以向右的横向一级失稳为例，分析计算采育机向右横向一级失稳的计算与判断方法。

2.1.1 横向一级稳定性计算

设平面EO2N 外法矢量(XEO2N，YEO2N，ZEO2N)，分别计算平面EO2N 内外法向量为=(1，a1，b1)=(－1，a2，b2)。

利用立体三角形中向量之间的夹角关系，判断平面EO2N 的外法矢量，并将相应的值赋给平面MON 的外法矢量(XEO2N，YEO2N，ZEO2N)。若·＞0，则(XEO2N，YEO2N，ZEO2N)=;若·＞0，则(XEO2N，YEO2N，ZEO2N)=。

2.1.2 横向一级稳定性判断

根据特征矢量法，判断采育机向右的横向一级稳定性。若ZEO2N＞0，则向右横向一级稳定性稳定;若ZEO2N=0，则向右横向一级稳定性倾翻临界状态;若ZEO2N＜0，则向右横向一级稳定性不稳定状态。

利用相同的计算方法，可计算并判断采育机向后的稳定性。设平面EO2M 外法矢量为(XEO2M，YEO2M，ZEO2M)，则:若ZEO2M＞0，向左横向一级稳定性稳定;若ZEO2M=0，向左横向一级稳定性倾翻临界状态;若ZEO2M＜0，向左横向一级稳定性不稳定状态。

2.2 横向二级稳定性计算与判断

轮式联合采育机，在发生横向一级失稳后会继续发生其他的失稳状态。以向右的横向一级失稳为例，转向角θ 为轮式联合采育机以方位角φ 置于斜坡上，发生横向向右的一级失稳。在发生横向向右的一级失稳后，除后桥外的整机质心将绕翻倾轴EN旋转，使摆动桥右侧两限位块相接触;由于除后桥外的质心的旋转，使得整机的质心因此偏转，此时即可判断轮式联合采育机是否会发生其他形式的失稳。分别以后轮接地点连线PQ 和两右轮QN 连线为翻倾轴，当旋转后的整机质心在PQ 以外时，采育机向后纵向翻倾;当旋转后的质心在QN 以外时，采育机向右横向二级失稳;当旋转后的质心在PQ 和QN 以内时，采育机将在一级失稳后保持稳定状态。

设平面EO3N 的外法向量为(XEO3N，YEO3N，ZEO3N)，分别计算平面EO3N 内外法向量为:n=(1，a1，b1)=(－1，a2，b2)。

利用立体三角形中向量之间的夹角关系，判断平面EO3N 的外法矢量，并将相应的值赋给平面EO3N 的外法矢量(XEO3N，YEO3N，ZEO3N)，若·＞0，则(XEO3N，YEO3N，ZEO3N)=;若·＞0，则(XEO3N，YEO3N，ZEO3N)=。

根据特征矢量法，判断采育机向右横向一级失稳后横向二级稳定性状态。若ZEO3N＞0，则向右横向二级稳定性稳定状态;若ZEO3N=0，则向右横向二级稳定性倾翻临界状态;若ZEO3N＜0，则向右横向二级稳定性不稳定状态。

利用相同的计算方法，可计算并判断采育机横向一级失稳后向后的稳定性。设平面PO3Q 外法矢量为(XPO3Q，YPO3Q，ZPO3Q)，则:若ZPO3Q＞0，则向右一级失稳后不会再发生向后翻倾失稳;若ZPO3Q=0，则向右一级失稳后处于向后翻倾失稳临界状态;若ZPO3Q＜0，则向后一级失稳后会继续再发生向后翻倾失稳;当ZPO3Q＞0，且ZQO3N＞0，则采育机向右横向一级失稳后，既不会发生向右横向二级失稳，也不会发生向后的纵向失稳，保持稳定状态。

同理，可采用相同的计算方法，建立采育机向左一级失稳后各失稳状态判断计算方法。

设平面PO4M 的外法矢量为(XPO4M，YPO4M，ZPO4M)，利用特征矢量法判断采育机向左横向一级失稳后横向二级稳定性。若ZPO4M＞0，则采育机向左横向一级失稳后不会发生横向二级失稳;若ZPO4M=0，则采育机向左横向一级失稳后处于横向二级失稳临界状态;若ZPO4M＜0，则采育机向左横向一级失稳向后发生横向二级失稳。

设平面PO4Q 的外法矢量为(XPO4Q，YPO4Q，ZPO4Q)，利用特征矢量法判断采育机向左横向一级失稳后纵向稳定性。若ZPO4Q＞0，则向后为稳定状态;若ZPO4Q=0，则向后为倾翻临界状态;若ZPO4Q＜0，则向后为不稳定状态;当ZPO4M＞0，且ZPO4Q＞0，则采育机向左横向一级失稳后，既不会发生向左横向二级失稳，也不会发生向后纵向失稳，保持稳定状态。

3 结束语

林木联合采育装备作为一种高性能的现代化林业复合装备，在人工林地作业，显示出无法比拟的先进性，为采伐工人提供了安全、舒适的工作环境，从而提高了生产效率和木材利用率［6］。目前，在国际林业采育行业的应用越来越广，显示出巨大的发展潜力。多功能林木采育装备在作业过程中的稳定性，是设计和实现人工智能化的重要指标，因此，对其稳定性的研究具有十分重要的现实意义和应用价值。

［1］ 赵文锐，刘晋浩.伐木联合机的现状及发展［J］.林业机械与木工设备，2008，36(11):10－12.

［2］ 鲍际平，刘晋浩，魏占国，等.世界采运机械的采伐方式及发展进程［J］.湖北农业科学，2009，48(8):2004－2006.

［3］ 王典，刘晋浩，王建利.基于系统聚类的林地内采育目标识别与分类［J］.农业工程学报，2011，27(12):173－177.

［4］ 王猛猛，鲍际平，刘晋浩.基于虚拟样机技术的联合采伐机静态稳定性分析［J］.湖北农业科学，2009，48(6):1485－1487.

［5］ 郭世怀，刘晋浩，孙治博，等.轮式林木联合采育机林地越障能力分析与仿真［J］.江苏农业科学，2013，41(8):387－389.

［6］ 魏占国，王忠伟，刘晋浩.基于现代设计技术林木联合采育机的设计及评价体系［J］.东北林业大学学报，2013，41(8):146－149.