三维装配几何约束组合的分类求解策略

黄学良， 李 娜， 陈立平

（1. 中国工程物理研究院总体工程研究所，四川 绵阳 621900；2. 华中科技大学国家CAD支撑软件工程技术研究中心，湖北 武汉 430074）

三维装配几何约束组合的分类求解策略

黄学良1， 李 娜1， 陈立平2

（1. 中国工程物理研究院总体工程研究所，四川 绵阳 621900；2. 华中科技大学国家CAD支撑软件工程技术研究中心，湖北 武汉 430074）

针对两个刚体之间的三维几何约束求解问题，依据几何约束的参数结构分析了角度约束和距离约束的解耦性，给出了角度约束和距离约束可解耦求解的条件；然后对两个刚体之间的几何约束进行组合分析，总结出约束度不小于2的几何约束构成的组合只有几十种，且均可采用几何推理方法进行求解；最后阐述了附加方向约束、冗余约束和矛盾约束对数值求解的不利影响，提出了三维几何约束组合的分类求解策略，并用实例验证了该求解策略的有效性。

几何约束；解耦性分析；冗余约束；几何推理

几何约束求解的基本思路是采用分而治之的方法将几何约束系统分解为若干个规模较小的子系统，然后分别对各个子系统进行求解，最后用各个子系统的解组装成整个几何约束系统的解[1]。针对三维装配几何约束系统，文献[2]提出的等价性分析方法可以将其分解为大量独立边子图对应的两个刚体之间的几何约束系统和独立闭环子图、耦合闭环子图对应的多个刚体之间的几何约束闭环系统，文献[3]提出的递归分解方法进一步将多个刚体之间的几何约束闭环系统分解为一系列两个刚体之间的几何约束系统，这使得对两个刚体之间几何约束系统的高效稳定求解成为三维几何约束求解的关键内容。目前，对于两个刚体之间的几何约束系统，除去稳定性不够的数值方法和求解效率不足的符号方法，几种具有代表性的求解方法分别是基于自由度分析的几何推理方法[4-6]、基于位姿解耦的分步增量求解方法[7-9]和面向特定构型的解析求解方法[10]，但这些方法均是针对两个刚体之间的特定几何约束问题的求解方法，缺乏对两个刚体之间几何约束问题的系统性分析和分类。为此，本文针对两个刚体之间的几何约束问题，分析角度约束和距离约束可解耦求解的条件，研究几何约束组合的分类，并据此提出基于约束组合分类的混合求解策略。

1 几何约束的参数结构分析

由三维几何约束的基本约束分量表达可知，两个刚体上几何实体之间的距离、角度、平行、垂直、相切和重合等三维几何约束均可表达为若干个基本几何约束的组合，且能够归为11类[11]，分别是约束度为1的5种基本几何约束（矢量角度约束、点点距离约束、点线距离约束、点面距离约束和线线距离约束），约束度为 2的矢量平行约束、线面距离约束和点线重合约束，约束度为3的点点重合约束和面面距离约束，约束度为4的线线重合约束。由于约束度大于1的几何约束可用约束度等于 1的基本几何约束的组合表示，而在这些基本几何约束中，角度约束和距离约束在参数结构上存在差异，角度约束只与表示刚体姿态的欧拉参数有关，而距离约束则与表达刚体姿态的欧拉参数以及表示刚体位置的点坐标都有关，刚体姿态的变动会同时影响角度约束和距离约束的满足，而刚体位置的变动则只会影响距离约束的满足，即刚体的位置变量只由距离约束确定。如果可以首先单独求解角度约束确定刚体的姿态，然后单独求解距离约束确定刚体的位置，就能将刚体上几何约束组合的整体求解转换为角度约束和距离约束的先后单独求解。

通过分析角度约束和距离约束的参数结构，可得到如下性质：

性质1：与动刚体U匹配的独立角度约束的数量小于或等于3。

性质2：如果与动刚体U匹配的独立角度约束的数量等于3，则角度约束和距离约束可解耦求解，首先求解角度约束和欧拉参数归一化约束确定表示刚体姿态的欧拉参数，然后求解距离约束确定刚体的位置参数。

性质3：如果与动刚体U匹配的距离约束的数量等于1，则角度约束和距离约束可解耦求解，姿态参数和位置参数可先后确定。

性质4：假定与动刚体U匹配的距离约束的数量为 m，如果满足条件 3＜m≤6，则角度约束和距离约束一定不能解耦求解，姿态参数和位置参数必须同时进行求解。

依据上述性质，按刚体上角度约束和距离约束的数量进行分类，可以得到不同有效约束数量的约束组合的解耦求解特性如表1所示。其中，mDnA表示该约束组合有m个有效距离约束和n个有效角度约束组成，“√”指可解耦求解，“×”指不可解耦求解，“?”指解耦求解性不确定。在表1中有21种约束组合，其中9种约束组合可解耦求解，6种约束组合不可解耦求解，另外 6种约束组合能否解耦求解无法由性质1～4确定。对于这6种解耦性无法确定的约束组合，存在性质5。

性质5：如果基刚体B和动刚体U之间只有一个几何约束，则该几何约束中的角度约束分量和距离约束分量是可解耦求解的。

上述性质依据角度约束和距离约束的数量关系来判定几何约束组合是否可解耦求解，其前提条件是几何约束组合中不包含冗余约束，即依据角度约束和距离约束的数量关系来判断之前必须先剔除冗余约束。

2 几何约束组合的分类

性质6：假定基刚体B和动刚体U之间只有点点重合约束、面面距离约束和线线重合约束这三类约束度≥3的几何约束，则基刚体B和动刚体U之间几何约束的数量≤3。

证明：如果刚体之间存在线线重合约束，由于线线重合的约束度为4，有4个基本约束分量，而刚体有6个自由度，由于每添加1个非冗余几何约束都将至少增加1个有效的基本约束分量，此时至多还可添加2个几何约束就能使刚体完全约束，那么基刚体B和动刚体U之间的几何约束数量≤3。如果刚体之间不存在线线重合约束，根据组合理论，刚体之间必然存在2个面面距离约束或是2个点点重合约束；如果是2个面面距离约束，则此时动刚体U只有1个移动自由度；如果是2个点点重合约束，则此时动刚体U只有1个转动自由度；显然，再添加1个几何约束必然使刚体完全约束，那么基刚体B和动刚体U之间的几何约束的数量≤3。得证。

依据组合理论，从点点重合约束、面面距离约束和线线重合约束这3类约束中任选2个构成的欠约束组合的数量最多有6种，任选3个构成的完整约束组合的数量最多有10种。图1所示为约束度≥3的几何约束的组合分类，图中RDOF(Residual Degree of Freedom)为受约束刚体的剩余自由度，RTDOF(Residual Translational Degree of Freedom)为受约束刚体的剩余移动自由度，RRDOF(Residual Rotational Degree of Freedom)为受约束刚体的剩余转动自由度，nDmA表示刚体上约束组合中有n个有效的距离约束分量和m个有效的角度约束分量。用 ΦCLL、分别表示线线重合约束、面面距离约束和点点重合约束，根据约束的几何分析，这16种约束组合中角度约束分量和距离约束分量可以解耦求解的约束组合实例有和角度约束和距离约束不能解耦求解的约束组合实例有和显然，对于那些依据数量分析无法确定解耦性的约束组合，通过几何分析可以确定其中的角度约束和距离约束是否可以解耦求解，比如约束组合）中的角度约束和距离约束可解耦求解。对于约束类型和约束数量均相同的几何约束组合，约束关联几何实体的特征参数差异也会导致其有效几何约束分量不尽相同，比如 2个线线重合约束构成的约束组合如果则刚体U只有沿直线的移动自由度，为实例否则，刚体 U 没有剩余自由度，为实例

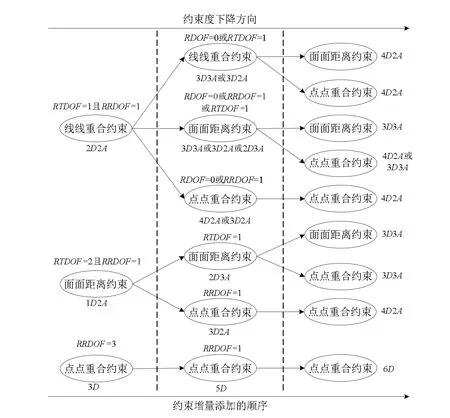
图1 约束度≥3的几何约束的组合分类

下面具体分析约束关联几何实体的特征参数的差异对几何约束组合中有效几何约束分量的影响。对于约束组合）的两个线线重合约束如果，则刚体U只有沿直线的移动自由度，为实例；否则，刚体U没有剩余自由度，为实例对于约束组合）的线线重合约束 CoiLL和面面距离约束 DisFF如果则刚体U只有绕直线的旋转自由度，为实例如果则刚体 U只有沿直线的移动自由度，为实例否则，刚体U没有剩余自由度，为实例对于约束组合）的线线重合约束 CoiLL和点点重合约束 CoiPP，如果点在直线上，则刚体U只有绕直线的旋转自由度，为实例否则，刚体U没有剩余自由度，为实例对于约束组合）的线线重合约束面面距离约束和CoiPP，如果则为实例如果则为实例由上述分析可知，任选两个约束度≥3的几何约束构成的约束组合，其有效约束度≥5；因此，有性质7。

性质7：如果基刚体B和动刚体U之间有两个几何约束属于线线重合约束、面面距离约束和点点重合约束这三类，则基刚体B和动刚体U之间几何约束的数量≤3。

根据性质7可知，如果刚体之间存在3个几何约束，且其中只有2个几何约束的约束度≥3，则另外1个几何约束可能是约束度等于2或约束度等于1的几何约束。约束度为2的几何约束有3种，则由2个约束度≥3的几何约束和1个约束度等于 2的几何约束构成的约束组合至多有6×3=18种；约束度等于1的几何约束有5种，则由2个约束度≥3的几何约束和1个约束度等于 1的几何约束构成的约束组合至多有 6×5=30种。由于角度约束分量只能与刚体的姿态变量匹配，刚体之间角度约束分量的数量必须满足性质1，故这两类约束组合的最大数量分别为 16和28。另外，受2个约束度≥3的几何约束的动刚体U至多有1个剩余移动自由度或1个剩余旋转自由度，如果将2个约束度≥3的几何约束构成的约束组合分为剩余移动自由度的约束组合和剩余旋转自由度的约束组合，则由2个约束度≥3的几何约束和1个约束度任意的几何约束构成的约束组合的数量为12+10=22；在这22种组合中，只有部分组合的角度约束和距离约束可解耦求解，但全部可以采用几何推理方法进行求解。

性质8：如果基刚体B和动刚体U之间存在1个线线重合约束，则基刚体B和动刚体U之间几何约束的数量≤3。如果基刚体B和动刚体U之间存在1个点点重合约束或面面距离约束，则基体B和动刚体U之间几何约束的数量≤4。

根据性质8给出的数量上界分析1个线线重合约束和2个约束度等于2的几何约束的组合分类、1个点点重合约束和3个约束度等于2的几何约束的组合分类以及1个面面距离约束和3个约束度等于2的几何约束的组合分类，发现三者总共有 33种约束组合，其中有大约一半的约束组合不可解耦求解，但可以采用几何推理方法进行求解。

3 几何约束组合的求解

3.1 附加方向约束对数值求解的影响

如图2(a)所示两个刚体B1和B2，平面F1和圆柱面F2在刚体B1上，平面F3和圆柱面F4在刚体B2上。欲获得如图2(c)所示的装配结果，可在刚体 B1和 B2之间添加反向共面约束CoiFF(F1,F3,-1 )和反向共轴约束 CoiLL(F2,F4,-1)，这2个几何约束的基本约束表达分别为：

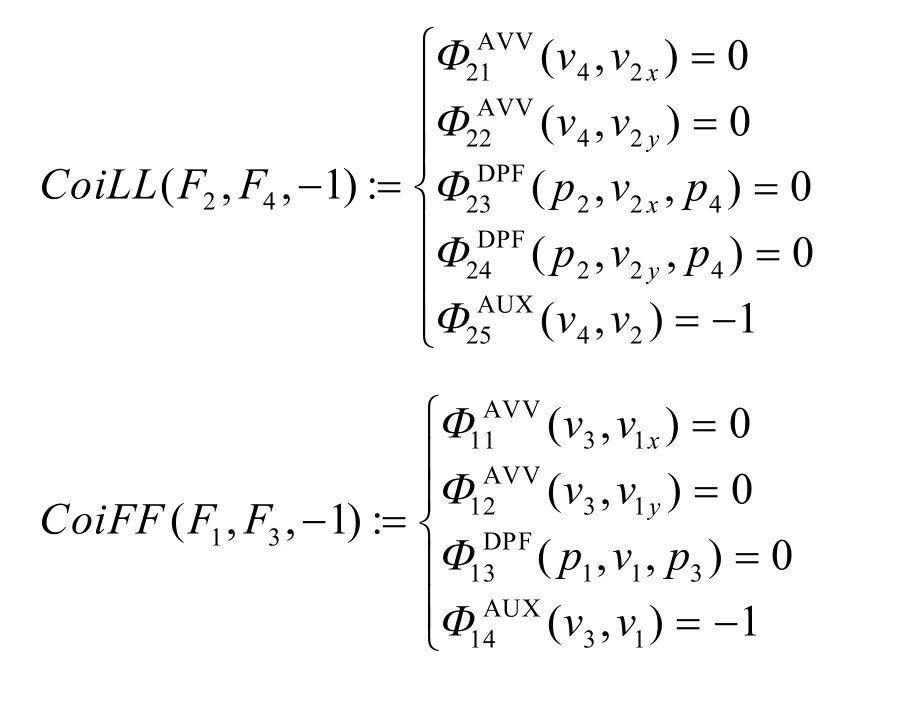
图2 在两个刚体之间添加1个共轴约束和1个共面约束

3.2 冗余约束和矛盾约束对数值求解的影响

如图3(a)所示，在刚体B1和B2之间依次添加3个共点约束CoiPP(p1, p4)、CoiPP(p2, p5)和CoiPP(p3, p6)，这3个共点约束的基本约束表达分别为：

假定首先添加CoiPP(p1, p4)，约束满足后刚体B2的位姿如图3(b)所示。然后添加CoiPP(p2, p5)，此时刚体 B2的位姿满足和( p.z, p.z)= 0，而冗余性分析必然认定2 5 CoiPP(p2, p5)的3个基本约束方程中存在1个冗余约束方程；如果将( p.y,p .y)= 0视为冗

2 5果如图3(c)所示，最后添加CoiPP(p3, p6)，此时刚体 B2的位姿满足基本约束方程( p.x,p .x) = 0和 ΦEY(p .y,p .y)= 0，而

3 632 3 6冗余性分析必然认定CoiPP(p3, p6)的3个基本约束方程中有 2 个是冗余的，如果将( p.z, p.z)= 0视为冗余的，则求解结果依

3 6然如图3(c)所示，而满足CoiPP(p3, p6)的正确结果应该是如图3(d)所示。可见，约束方程数值求解的正确性有赖于冗余约束判定的正确性。此外，如果将共点约束CoiPP(p3, p6)改为CoiPP(p6, p7)，由于共点约束CoiPP(p6, p7)与CoiPP(p1, p4)、CoiPP(p2, p5)是相互矛盾的，数值求解必然失败。但是，与冗余约束不同，数值求解失败并不能断定共点约束CoiPP(p6, p7)是矛盾约束，因为数值求解失败也可能源于数值算法的内在缺陷。可见，冗余约束和矛盾约束的存在增加了数值方法求解几何约束问题的复杂性。

图3 在两个刚体之间添加3个共点约束

3.3 几何约束组合的分类求解策略

对于包含线线重合约束、面面距离约束和点点重合约束的几何约束组合，直接采用几何推理方法进行解析求解。对于不包含线线重合约束、面面距离约束和点点重合约束的几何约束组合，首先剔除约束组合中的冗余约束，然后分析角度约束分量和距离约束分量的数量；若能解耦求解，则先求解角度约束，后求解距离约束；若不能解耦求解，则采用数值方法进行求解；如果不能确定是否能解耦求解，则先假设角度约束和距离约束可解耦求解，先求解角度约束，后求解距离约束，若求解距离约束失败，则可确定该约束组合不能解耦求解，重新采用数值方法进行求解，数值求解时考虑冗余约束和附加方向约束。

4 实例分析

如图4(a)所示的变速箱三维装配几何模型，其装配几何约束图经等价性分析处理后如图4(b)所示。由性质 6～8及其分析可知，在所有的 36个刚体之间，只有 3种类型的约束组合，其中类型的约束组合有 28个，类型的约束组合有 5个，类型的约束组合有1个，若是考虑装配设计过程中增量添加几何约束的方式，则除上述3种类型的约束组合外，还有4种类型的约束组合，分别为和

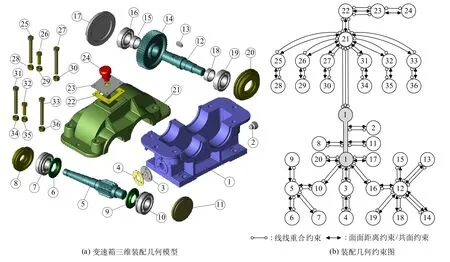
图4 变速箱三维装配模型及其几何约束图

5 结 论

本文通过分析角度约束和距离约束的结构参数特点，给出了两个刚体之间的几何约束系统中角度约束和距离约束的可解耦求解条件，揭示了大量常见几何约束组合是不可解耦求解的。基于约束度不小于2的三维几何约束只有6种的事实，对两个刚体之间的几何约束组合进行分析，总结出约束度不小于2的几何约束构成的组合只有几十种，且可采用几何推理方法进行求解。通过阐明附加方向约束、冗余约束和矛盾约束对数值求解的不利影响，指出采用几何推理方法解析求解两个刚体之间的几何约束系统具有突出的优势，并据此给出了基于约束组合分类的混合求解策略。由于对几何约束组合进行了系统性的分类，针对不同的问题采用特定的求解方法，该求解策略可以获得更高的求解效率和稳定性。

[1] 高小山, 蒋 鲲. 几何约束求解研究综述[J]. 计算机辅助设计与图形学学报, 2004, 16(4): 385-396.

[2] 黄学良, 王波兴, 陈立平, 黄正东. 三维几何约束系统的等价性分析[J]. 软件学报, 2011, 22(5): 1106-1120.

[3] 黄学良, 李 娜, 陈立平. 三维装配几何约束闭环系统的递归分解方法[J]. 计算机辅助设计与图形学学报, 2013, 25(9): 1296-1303.

[4] Kramer G. Using degrees of freedom analysis to solve geometric constraint system [C]//Proceedings of the First ACM Symposium on Solid Modeling Foundations and CAD/CAM Applications. New York: ACM Press, 1991: 371-378.

[5] 乔 雨, 王波兴, 向 文. 基于自由度分析的三维几何约束推理求解[J]. 计算机辅助设计与图形学学报, 2002, 14(6): 557-561.

[6] 姜 勇, 王波兴, 陈立平. 三维几何约束求解的自由度归约算法[J]. 计算机辅助设计与图形学学报, 2003, 15(9): 1128-1133.

[7] Kumar A V, Yu Lichao. Sequential constraint imposition for dimension-driven solid models [J]. Computer-Aided Design, 2001, 33(6): 475-486.

[8] 石志良, 陈立平, 王小刚. 三维装配约束推理的球面几何和球面机构法[J]. 计算机辅助设计与图形学学报, 2006, 18(7): 942-947.

[9] 石志良, 陈立平. 装配位置约束建模及求解[J]. 计算机辅助设计与图形学学报, 2007, 19(5): 553-557.

[10] Kim J, Kim K, Chio K, Lee J Y. Solving 3D geometric constraints for assembly modeling [J]. The International Journal of Advanced Manufacturing Technology, 2000, 16(11): 843-849.

[11] 黄学良, 陈立平, 王波兴, 黄运保. 面向集成变量化设计的三维几何约束求解方法[J]. 计算机辅助设计与图形学学报, 2010, 22(1): 30-36.

Classification and Solution of 3D Assembly Geometric Constraint System Between Two Rigid Bodies

Huang Xueliang1, Li Na1, Chen Liping2
(1. Institute of Systems Engineering, CAEP, Mianyang Sichuan 621900, China; 2. National CAD Support Software Engineering Research Center, Huazhong University of Science and Technology, Wuhan Hubei 430074, China)

It is a key problem to solve the geometric constraint system between two rigid bodies(GCSBTRD) efficiently and stably when 3D geometric constraint system has been decomposed into a series of GCSBTRDs using equivalent constraint substitution method. In this paper, the decoupling conditions to separately solve angle constraints and distance constraints of GCSBTRDs are presented after analyzing the parametric structure of angle constraints and distance constraints. Then, with the geometric analysis of GCSBTRDs, it is found that the GCSBTRDs consisting of the geometric constraints with more than one constraint degrees can be divided into dozens of patterns, which can all be solved analytically by geometric reasoning method. Subsequently, the adverse impact on numerical solution of GCSBTRDs from additional direction constraint, redundant constraint and contradictory constraint is addressed to demonstrate the advantage of geometric reasoning method. Finally, a hybrid solving strategy based on the classification of constraint combinations is proposed to solve GCSBTRDs, whose effectiveness has been validated by a practical example.

geometric constraint; decoupling analysis; redundant constraint; geometric reasoning

TP 391

A

2095-302X (2014)02-0236-07

2013-06-13；定稿日期：2013-09-13

国家自然科学基金资助项目（51375185）；中国工程物理研究院总体工程研究所创新与发展基金资助项目（13cxj19）

黄学良（1983-），男，江西崇仁人，工程师，博士。主要研究方向为几何约束求解、变量化直接建模、虚拟样机和 CAD/CAE集成。E-mail：xueliang.huang@qq.com

陈立平（1964-），男，湖北武汉人，教授，博士，博士生导师。主要研究方向为几何约束求解、参数化设计、多体系统动力学、多领域建模与仿真。E-mail：chenlp@hustcad.com