最小势能原理在关键层挠度计算中的应用

张忠厚，左 彪，黄厚旭

(1.辽宁工程技术大学理学院，辽宁阜新 123000;2.辽宁工程技术大学力学与工程学院，辽宁阜新 123000;3.辽宁工程技术大学土木与交通学院，辽宁阜新 123000)

0 引言

钱鸣高提出了采场上覆岩层活动的关键层理论并用弹性组合梁模型确定了当较软岩层与坚硬关键层协调变形时关键层上的等效荷载［1］，李文秀等用弹性薄板法建立了开采时地表下沉的预测力学模型［2］，刘开云等利用弹性薄板法分析了采空区上覆岩层的组合运动特征并对关键层的位置进行了计算分析［3］。利用弹性板理论研究顶板挠曲变形已经取得了许多有价值的成果［3-6］。但在顶板挠度计算中已有的研究大多是先建立薄板力学模型然后求解平衡方程，本文将试图从另一个角度求解离层挠度问题。最小势能原理表明:在合外力作用下真实存在的位移场使平衡体系所具有的势能最小。将覆岩顶板简化为四边简支的弹性薄板然后建立平衡方程求解弹性薄板在上部荷载及自重下的挠度值是目前研究覆岩离层及地表沉陷使用较多的一种方法。在上部荷载及自重作用下四边简支的弹性顶板的挠曲方程符合双三角级数。注浆减沉的力学机理是:浆体充填离层空间，固结后对关键层提供支撑反力进而减小地表沉降。本文将以最小势能原理为基础计算关键层在注浆前后的最大挠度值，并用求得的结果评价注浆减沉的效果。

1 离层岩板弹性力学模型建立

在开采形成采空区后位于采空区上部的岩石失去下部支撑，在上部荷载及自重作用下将发生向下的挠曲变形。由于成岩年代、岩石成分及上覆荷载等存在差异，在下沉过程中不同岩板将产生不同的挠度。关键层对岩体的活动起全部的控制作用受关键层控制的各岩层将与关键层协调变形且挠曲形式相同。在离层空间上方关键层岩板的悬露面积远大于其厚度，而关键层的硬脆性决定了在未破坏范围内关键层将发生弹性变形且其挠度小于其厚度，因此将关键层岩板简化为弹性板是合理的。且根据已有的研究成果可将关键层岩板简化为四边简支的矩形岩板。在应用弹性薄板理论分析关键层的离层变形之前先对关键层做如下假设［7］:(1)垂直于薄板中平面的法线在变形后仍为垂直弹性曲面的直线且长度不变;(2)垂直于中平面方向的正应力与其他两个方向的正应力相比可以忽略，即σz=0;(3)板的中平面无伸缩变形。

由弹性薄板理论知，薄板在合外力作用下的平衡方程为:

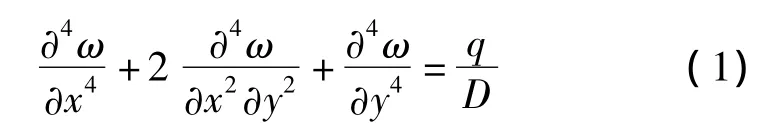
或表示为:

其中:

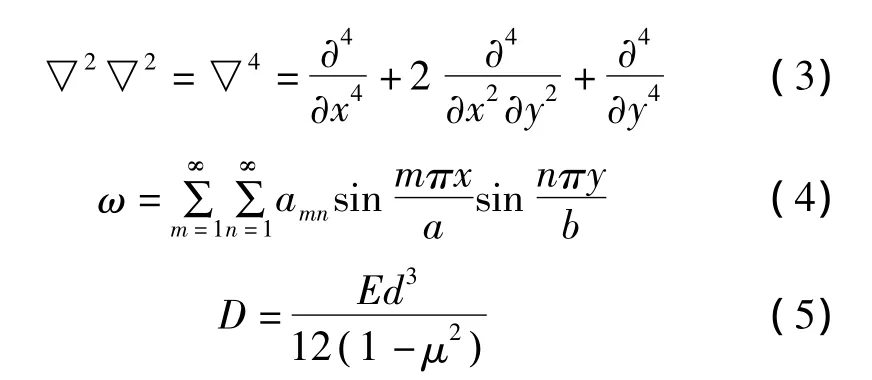
其中amn为关键层在弹性限度内的最大挠度，m、n分别为岩板在x、y方向挠曲的半波数，其中m、n=1、2…，a、b分别为岩板在 x、y方向的长度，q为关键层上的等效均布荷载，D为关键层的抗弯刚度，E为关键层岩板的弹性模量，μ为关键层岩板的泊松比，d为岩板厚度。

2 关键层上等效均布荷载q的计算

将关键层当作覆岩挠曲变形的分界点，与关键层协调变形的上覆岩层与关键层形成一个组合梁，依据岩层的自然分层将采场上覆岩层从下至上分别编号1、2、3…m … k，k ＞m 对应的厚度分别为 d1、d2、d3… dm… dk，密度分别为 ρ1、ρ2、ρ3…ρm…ρk，并假设第 m 层为关键层(图1)。则第m层至第k层将发生相同挠曲变形并且各层之间紧密接触这种变形协调关系可表示为:

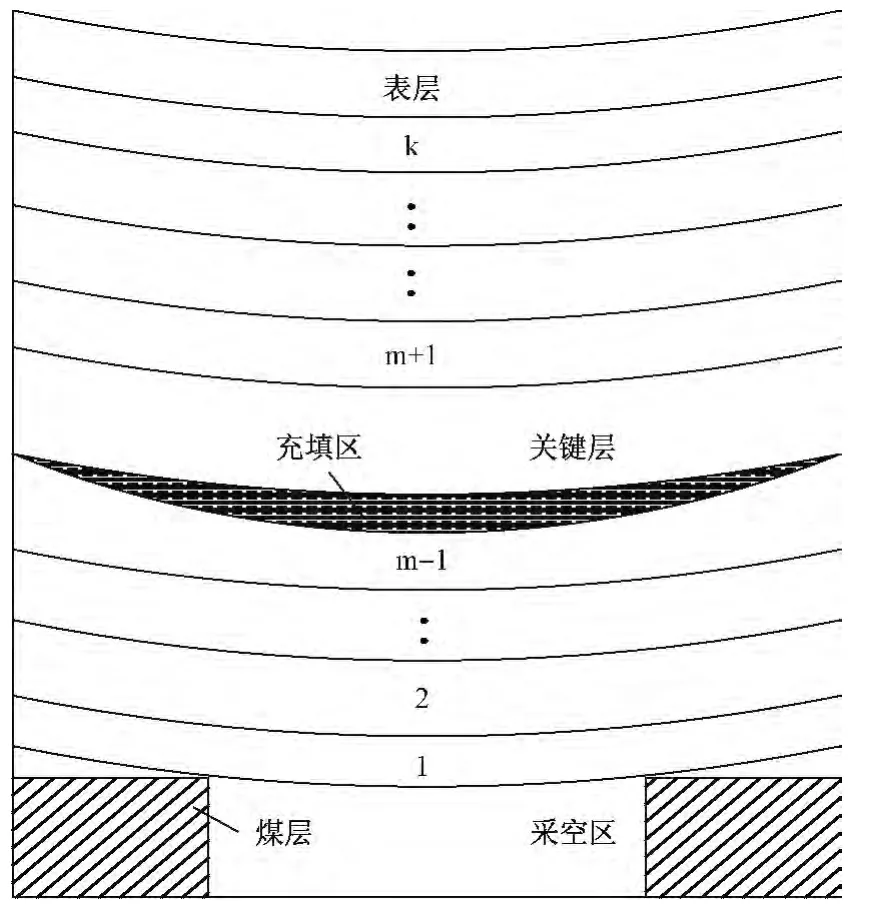
图1 覆岩离层力学模型Fig.1 Mechanical model of cover rock seperation stata

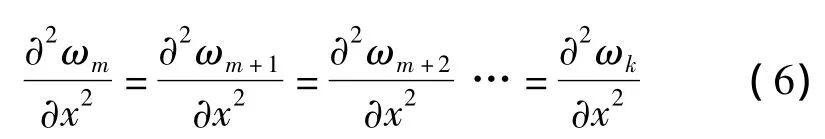
由材料力学知:

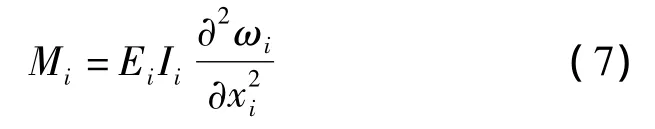
即:

将(8)代入式(6)得:

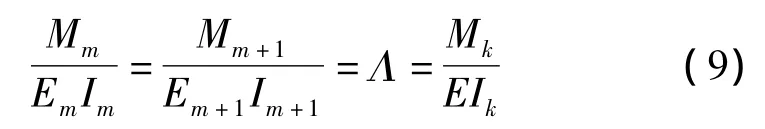
由式(9)可解得:

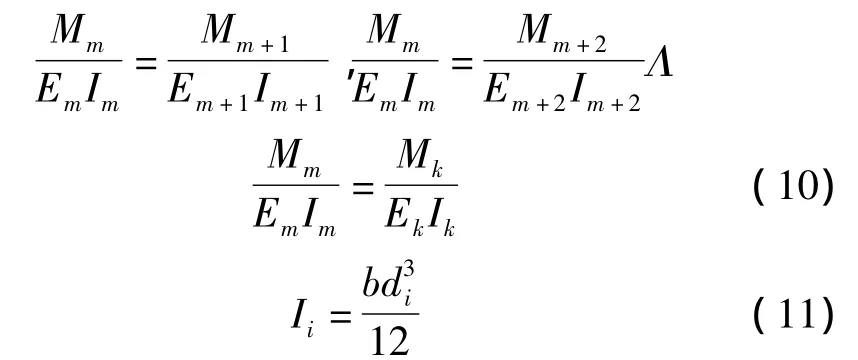
式中Mi(i=m…k)为第i层岩板承受的弯矩，Ii第i层岩层的截面惯性矩。由组合梁理论知:

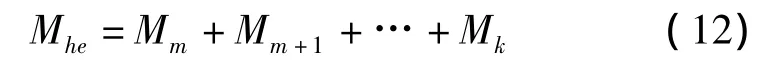
式中Mhe代表组合梁承受的总弯矩。

将式(10)代入式(12)可得:

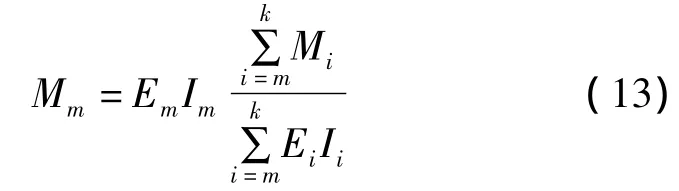
由于组合梁的弯矩可视为由组合梁上的均布荷载组成，则有:

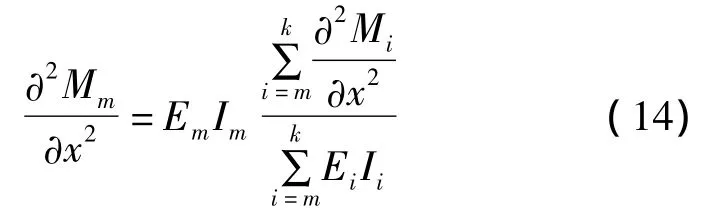
即:

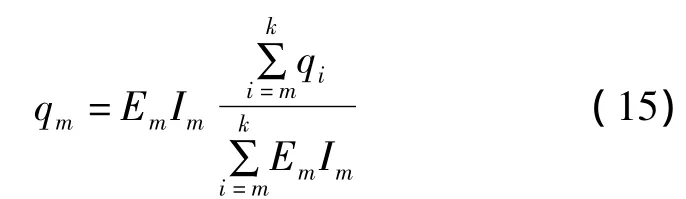
由qisi=ρisidig得:

式中si为相应岩板的有效计算面积。

将式(16)代入式(15)可得:

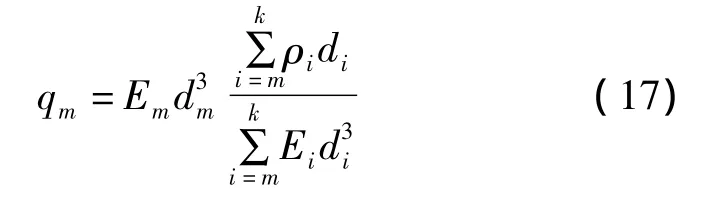
3 关键层的最大挠度计算

3.1 注浆前关键层的最大挠度计算

由于离层的产生是一个长期而缓慢的过程，因此可将关键层视为在合外力作用下的平衡体系.设在上部荷载及自重作用下关键层产生的最大挠度为amn。

当关键层发生挠曲ω后所具有的弹性势能为:

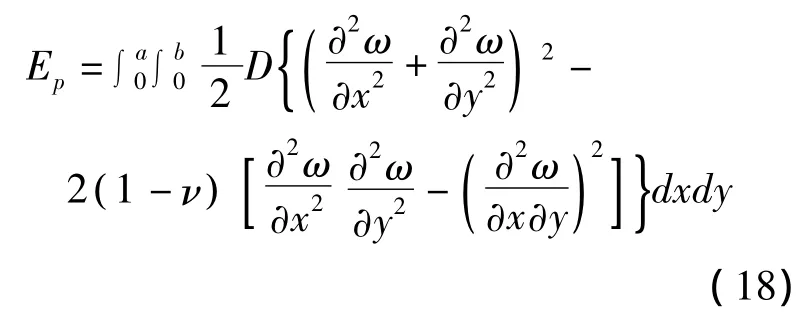
但由于关键层处于四边简支状态，因此上式中第二项将不存在，所以此处关键层的势能表达式为:

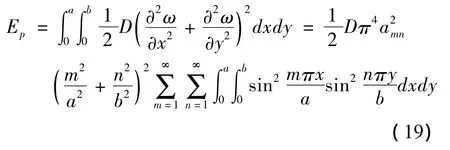
其中:

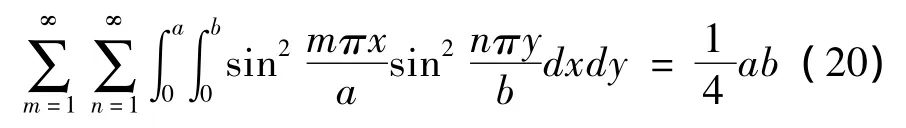
将式(20)代入式(19)中，则有:

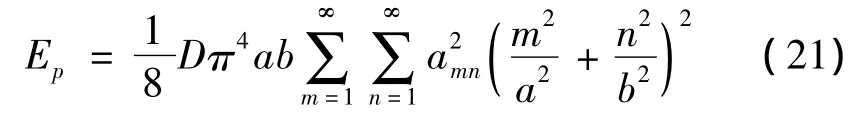
关键层上等效均布荷载在挠曲方向上做的功为:

关键层岩板所具有的总势能为:

将式(21)和(22)代入(23)中，则有:

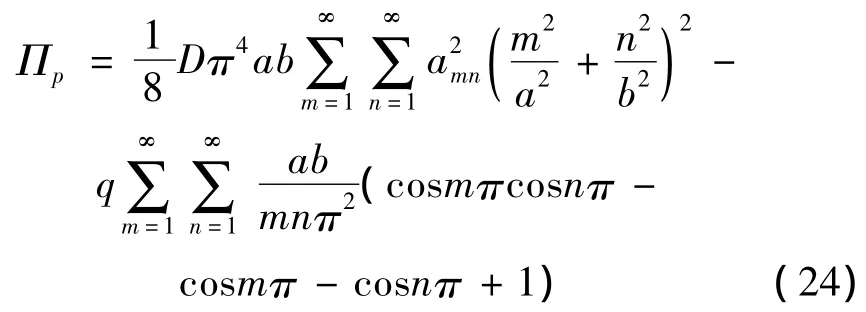
最小势能原理表明:对于给定的应力场平衡体系将发生让系统总势能最小的实际位移，则此时的位移amn应满足:

将式(24)代入式(25)中，则有:

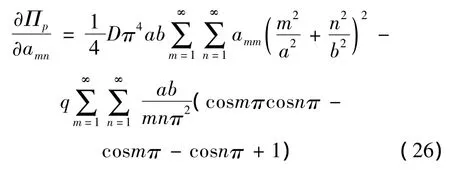
由式(21)可知:

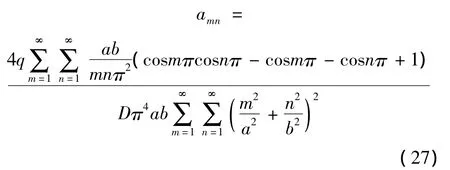
若仅取级数的第一项，即m=1，n=1则得关键层的最大挠度为:

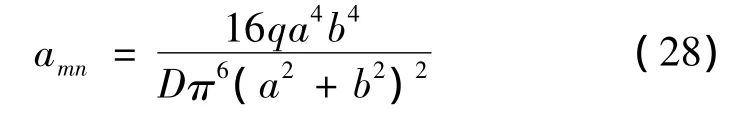
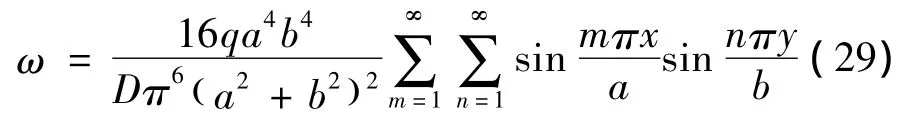
3.2 注浆后关键层的最大挠度计算

在离层空间中充填的粉煤灰浆体在固结后由于其硬度和弹性模量远小于坚硬的关键层顶板，因此可将固结后的浆体视为处于关键层下的弹性垫层。假设注浆时关键层只发生了大小可以忽略的挠曲下沉且注浆量足够，关键层的下沉和凝固浆体的变形是同步且两种介质之间接触良好，由Winkler地基假设知固结的浆体对关键层的支撑反力为［7］:

式中F是关键层受到的支撑反力，K是Winkler地基系数与基础本身的结构及力学特性有关，弹性地基系数K=(E0/h0)-2，其中E0，h0分别为垫层的弹性模量和厚度。ωz为注浆后关键层的挠度，由于支撑反力方向与ωz的方向相反，故F的值取负号。

注浆后关键层仍处缓慢下沉状态，但由于变形速率慢，因此可以将挠曲变形过程看作平衡状态。当关键层发生最大挠度amnz时具有的弹性势能为:

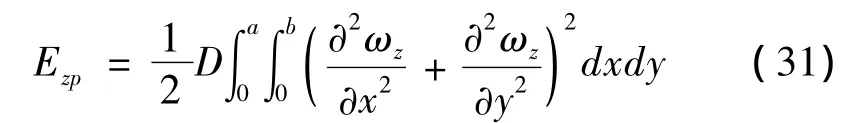
关键层的挠曲方程可表示为:

由式(21)知:

此时合外力做功为:

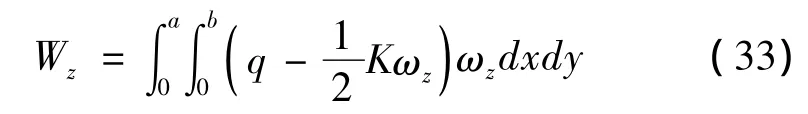
将式(20)和(22)代入式子(33)则有:

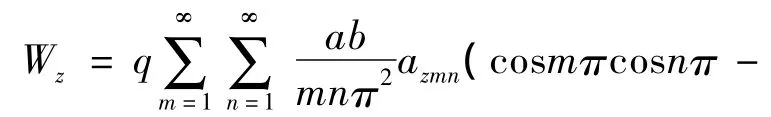
注浆后关键层的总势能为:

将式(32)和(34)代入(35)中则有:

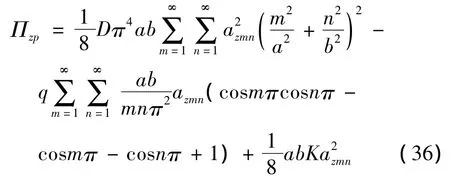
由平衡体系满足最小势能原理则有:

将式(36)代入式(37)中则有:

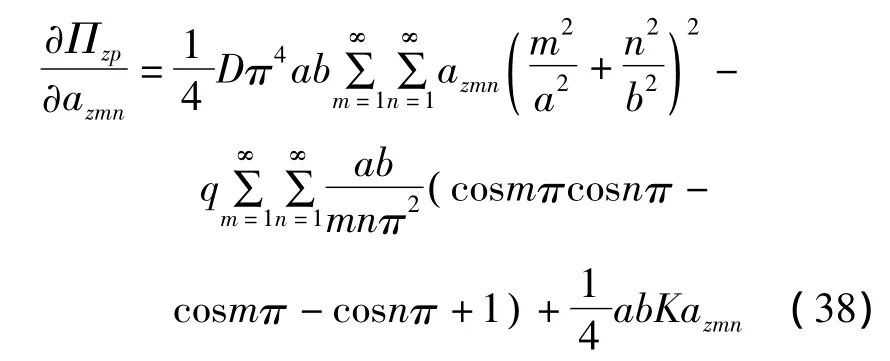
经整理后得:

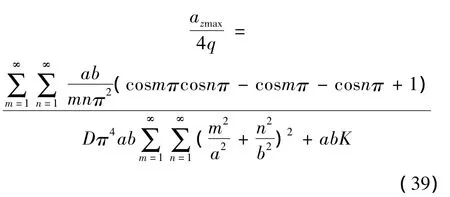
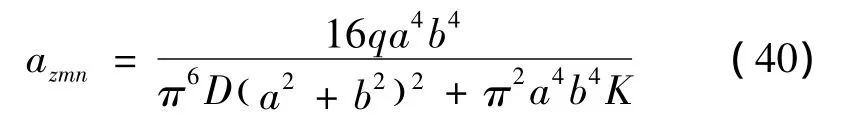
因此充填注浆后关键层的挠曲方程可以表示为:

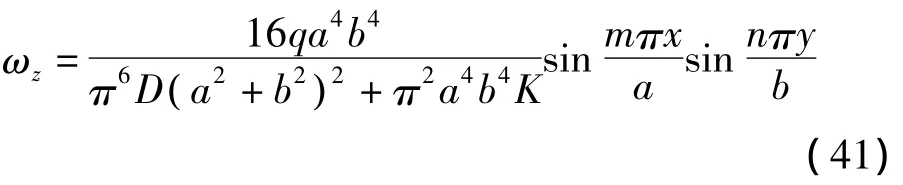
在式(39)中仅取级数第一项，当m=n=1得:

4 注浆减沉效果分析

4.1 薄板所受最大拉力方向的确定

由于注浆前后岩板的变形都是处于小挠曲变形范围内，因此可认为中平面依然保持为平面［7］。则岩板沿x、y方向的应力分别为:

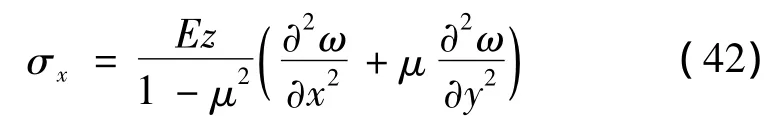
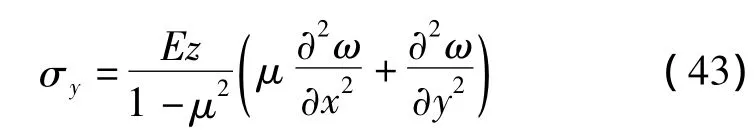
式中μ为岩板材料的泊松比且μ＜1，z为受力点距中平面的距离，在中平面上部时取“+”号，在中平面下部时取“-”号。由于最大拉应力出现在关键层最底端，即分别代入式(36)和(37)则得到最大拉应力σx、σy的表达式为:

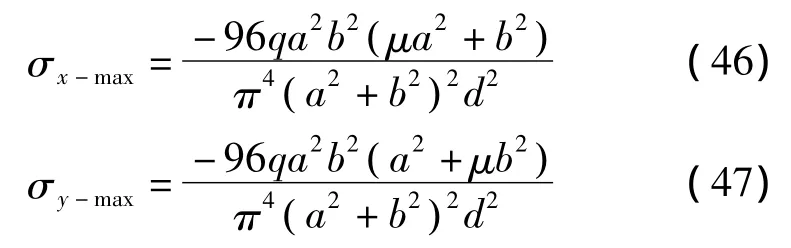
在式(46)和(47)中当改变 a、b的相对大小时得:

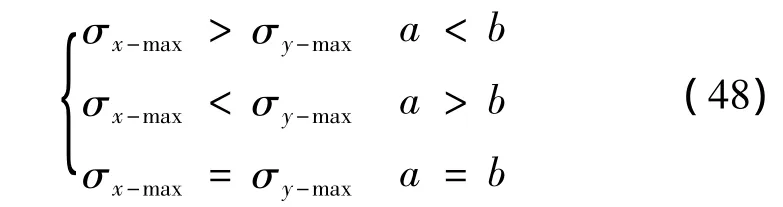
上式表明四边简支矩形岩板的最大拉应力发生在挠度最大处且沿顶板的短边方向。

4.2 关键层岩板的极限跨距的计算

在计算薄岩板挠度时应保证计算是在岩板的极限跨距内进行且满足，但实际开采中大多数情况下离层岩板的a、b值都大于岩板的极限跨距，因此必须对岩板极限挠度计算公式予以修正。弹性力学中将受到外部荷载作用时薄岩板最大挠度处正好发生拉裂时对应的长度称为薄岩板的极限跨距，分别用am、bm表示。薄岩板的极限跨距与岩板自身的力学性质、外观尺寸以及作用于岩板上的荷载的分布情况等都有关系，由板的抗拉强度可推导计算am、bm的公式为:［8］

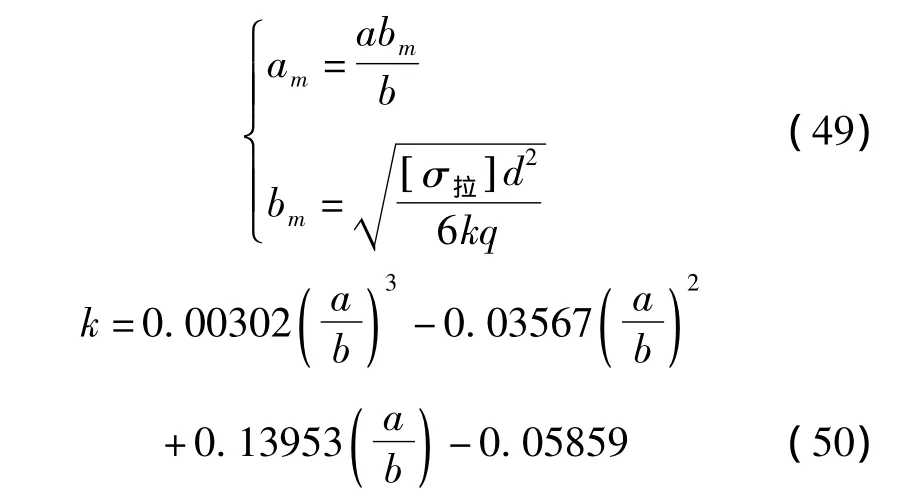
式中k为薄岩板的形状系数，由am、bm的表达式

可知薄岩板的抗拉强度是影响薄岩板极限跨距的主要因素。

将am、bm代入式(28)和(40)中可得关键层注浆前后的最大挠度分别为:

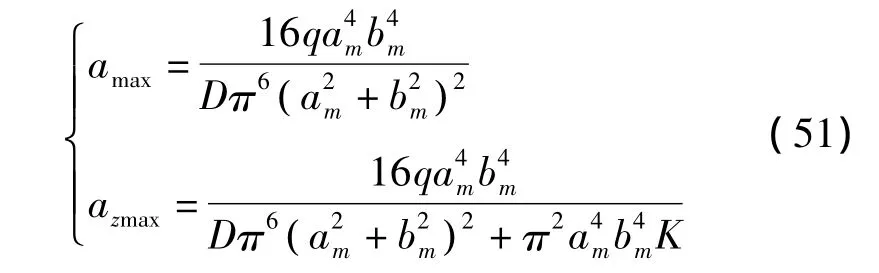
将式(51)代入式(29)和(41)中可得关键层注浆前后的挠度表达式为:

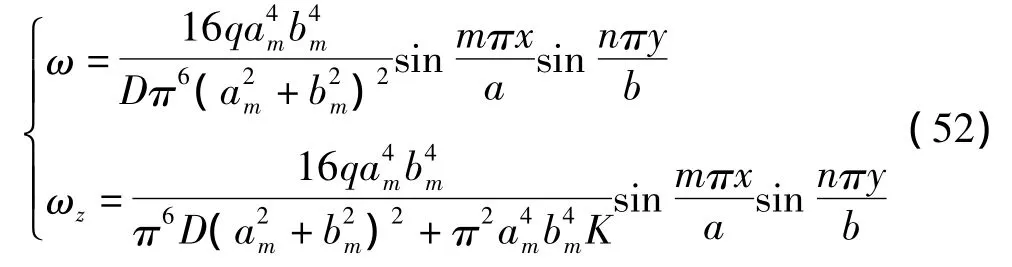
工程实际中常用注浆前后地表最大沉降值的变化作为衡量地表减沉的主要指标，考虑注浆是将浆液注入导水裂隙带之上的离层中，因此离层的下位岩层必须完整没有破坏，即该岩层不处于冒落带或断裂带范围之内。假设地表土层对因岩板挠曲而产生的沉陷的弱化作用可以忽略，关键层的挠曲变形可以最大限度的传递到地表，地表的最大沉降值和关键层的最大挠度相等，那么注浆的减沉效果就可以表示为:

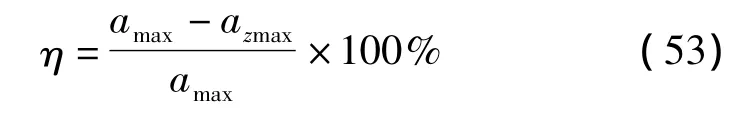
将式(51)代入式(53)中可得到离层注浆减沉系数的计算公式为:

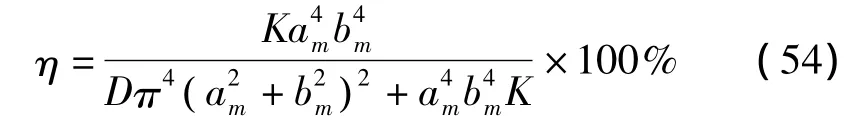
4.3 实例计算

某矿43下02工作面是四采区开采的第一个工作面，开采3下煤层。该工作面位于北翼3下回风大巷东320m。工作面走向长800m，斜长180m，煤层厚度1.98～5.30m，平均4m，含夹矸一层，最厚达1.2m。煤层倾角3°～15°，平均8°开采深度 556～588m，平均572m，各岩层力学性质见表1。

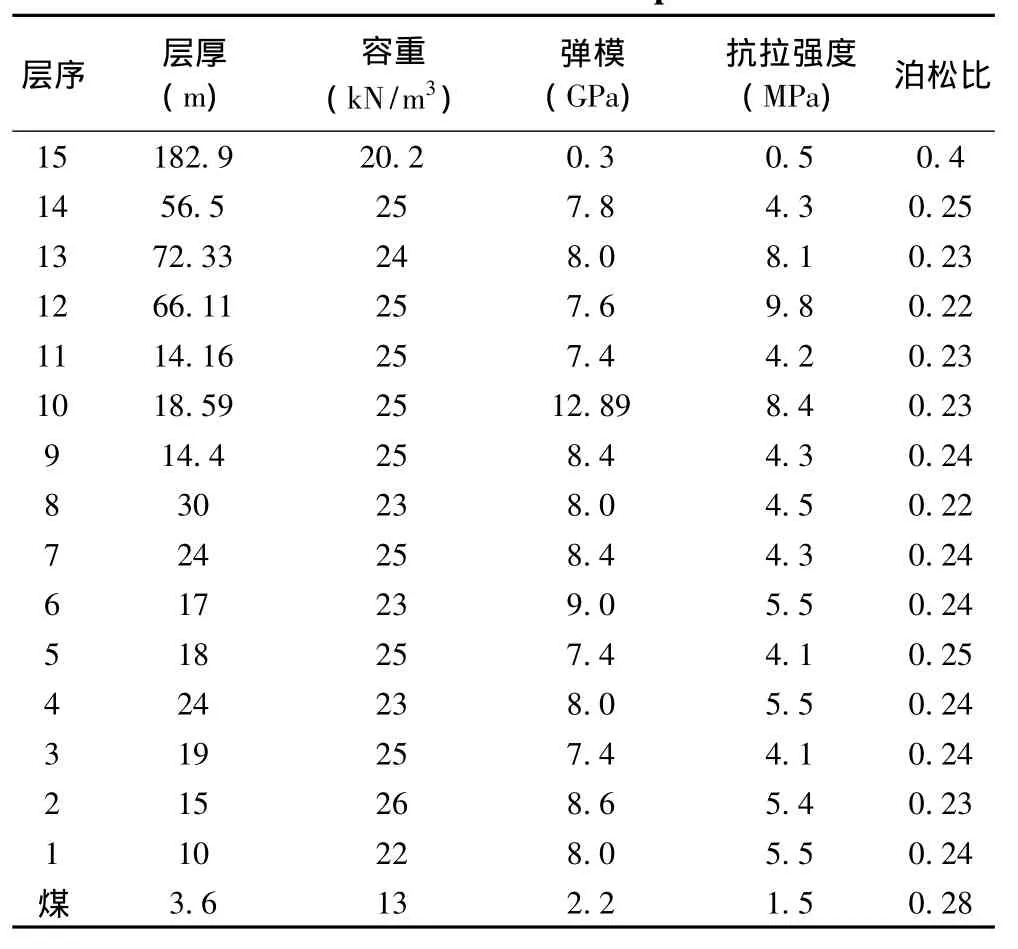
表1 岩层特性参数Table 1 Rock characteristic parameters

由上表岩石参数，通过覆岩关键层位置的快速判别［9］可确定岩层10为关键层。因为离层注浆是将浆液注入导水裂隙带之上的离层中，所以必须确保离层的下位岩层完整，即下位岩层不发生破坏，否则该岩层将位于冒落带或断裂带范围内［10］。故关键层的极限跨距尺寸取决于离层下位岩层的极限跨距尺寸。故此实例中关键层的极限跨距尺寸取决于岩层9，由工作面采矿条件分析知H=572m，a/b=4。将岩层9的相关参数代入式(49)后可以得到am=232m，bm=58m由式(17)及表1中数据可算得D10=7286.42GPa·m3。

表2 粉煤灰在封闭空间中的力学参数［11］Table 2 Mechanical parameters of fly ash

将注浆材料粉煤灰作取样实验，结果表明其弹性模量 E处于 0.03～0.05GPa之间，此处取 E=0.04GPa，经过计算上覆岩层相邻两岩板间的最大离层空间高度为h0max=1.2m，而实际注浆范围可等效为长和宽分别为800m和200m，面积S=160000m2的矩形，经计算离层空间的大小为 V=68947m3［11］，假设注采比合适且浆液刚好注满离层空间，将固结的注浆体看作一个矩形的薄板铺在关键层之下，则薄板厚度等于注浆体的平均厚度为h0=V/S，计算得到h0=0.43m。取h0=0.43m，E=0.04GPa计算后可得等效地基系数为 K=0.025GPa/m，将am=232m，bm=58m，D10=7286.42GPa·m3代入式(54)得离层注浆的减沉率为 η=26.1%，这与注浆减沉的实际效果相符［12］。

如图2所示，当最接近地表的关键层和此关键层对应的极限跨距为am=232m，bm=58m时，离层注浆的减沉效果随注浆体固结后形成的下卧支撑体的等效地基系数的增大将逐渐提高。且等效地基系数K从0增加到0.3时减沉系数η快速增长并超过0.8，因此，当等效地基系数K处于该范围时增大K能明显提高减沉效果;当等效地基系数K大于0.8时减沉系数增长缓慢，此范围内K的增大对减沉效果的影响不明显;而下卧支撑体的等效地基系数K主要与灌注材料的性质、级配、含水率有关，在其他条件不变的情况下材料的弹性模量越高，地基系数K越大，材料级配越均匀密实，地基系数K越大，含水率达到最佳时，地基系数K最大。然而实际减沉效果ηd往往达不到理想效果η，实际工程中，由于不同的填充条件和物理环境，之间为了提高加固效果，获得更好的减沉效果，注浆前应先分析离层动态运动规律，合理设计布置注浆钻孔，计算填充材料的注入量，注浆时可以适当提高注浆压力(充填材料反力大，也就是充填密实)。浆液比重最好为1.1～1.2t/m3，比重太大，不易输送灌注，且易堵塞注浆管，比重太小，材料沉缩率大，影响加固减沉效果。

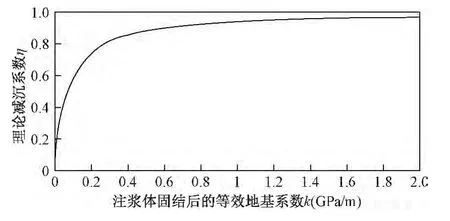
图2 等效地基系数K和减沉效果η的关系曲线Fig.2 The relationship of the equivalent foundation coefficient K and the reduce sink effect η

5 结论

(1)建立了开采后关键层的力学模型。将缓慢下沉并最终达到稳定的关键层岩板看作平衡体系，依据平衡体系具有最小势能的原理求出了关键层注浆前后的最大挠度。

(2)顶板发生挠曲变形时，在岩板的最大挠度处沿其短边方向将出现最大拉应力。

(3)将注浆前后关键层最大挠度的变化量间接描述地表的沉陷值，从而建立注浆减沉效果的评价模型，得出了注浆减沉评价的一般表达式。

(4)注浆前应先分析离层动态运动规律，合理设计布置注浆钻孔，计算填充材料的注入量，注浆时可以适当提高注浆压力(充填材料反力大，也就是充填密实)。

［1］钱鸣高，缪协兴，许家林.岩层控制中的关键层理论研究［J］.煤炭学报，1996，21(3):225-230.QIAN Minggao，MIU Xiexing，XU Jialin.Theoretical study of key stratum in ground control［J］.Journal of China Coal Society，1996，21(3):225-230.

［2］李文秀，梁旭黎，赵胜涛，等.地下开采引起地表沉陷预测的弹性模版法［J］.工程力学，2006，23(8):177-181.LI Wenxiu，LIANG Xuli，ZHAO Shengtao，et al.The elastic-thin-plate bending method for predicting ground subsidence due to undergroundmining［J］.Engineering Mechanics，2006，23(8):177-181.

［3］刘开云，乔春生，周辉.覆岩组合运动特征及关键层位置研究［J］.岩石力学与工程学报，2004，23(8):1301-1306.LIU Kaiyun，QIAO Chunsheng，ZHOU Hui.Research on combined motion characteristics of overlying rock stratum and position of key strata［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23(8):1301-1306.

［4］郝延锦，吴立新，戴华阳.用弹性板理论建立地表沉陷预计模型［J］.岩石力学与工程学报，2006，25(增1):2958—2962.HAO Yanjin，WU Lixin，DAI Huayang.Establing a ground settlement prediction model with elastic slab theory［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25(S1):2958-2962.

［5］王红卫，陈忠辉，杜泽超，等.弹性薄板理论在地下采场顶板变化规律研究中的应用［J］.岩石力学与工程学报，2006，25(S2):3769—3774.WANG Hongwei，CHEN Zhonghui，DU Zechao，et al.Application of elastic thin plate theory to changerule of roof in underground stope［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25(S2):3769-3774.

［6］翟所业，张开智.用弹性板理论分析采场覆岩中的关键层［J］.岩石力学与工程学报，2004，23(11):1856-1860.ZHAI Suoye，ZHANG Kaizhi.Analysis on key layer of overlying strata with elastic slab theory［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23(11):1856-1860.

［7］曲庆璋，章权，季求和，等.弹性板理论［M］.北京:人民交通出版社，1999.QU Qingzhang，ZHANG Quan，JI Qiuhe，et al.Theory of elastic plates［M］.Beijin:China Communications Press，1999.

［8］李小强，白世伟，李铀.最小势能原理在二维边坡稳定分析中的应用［J］.岩土力学，2004，25(6):909-912.LI Xiaoqiang，BAI Shiwei，LI You.2D slope stability analysis using principle of minimum potential energy［J］.Rock and Soil mechanics，2004，25(6):909-912.

［9］杨本生，张磊.覆岩关键层位置的快速判别及来压预测［J］.煤炭工程，2013(7):79-81.YANG Bensheng，ZHANG Lei.The distinguish and forecast of the place of the key cover stratum［T］Coal Engineering，2013(7):79-81.

［10］苏仲杰，于广明，杨伦.覆岩离层变形力学模型及应用［J］.岩土工程学报，2002，24(6):778-781 SU Zhongjie，YU Guangming，YANG Lun.Application of mechanicalmodel to deformation of covered rock separation strata［J］.Chinese Journal of Geotechnical Engineering，2002，24(6):778-781.

［11］苏仲杰.采动覆岩离层变形机理研究［D］，阜新:辽宁工程技术大学，2001.SU Zhongjie.Research of deformation mechanism of mining overburden separated strata［D］.Fuxin:Liaoning Technical University，2001.

［12］Palaski J.The experiment and practical results of applying backfill［C］∥Innovations in Mining Backfill Technology，Proceedings of 4th Intemational Symposium 011 Mining with Backfill，Montreal:［s.n］，1989:33-37.