吴家沟尾矿库堆积坝稳定性分析

谢园丁，吴庚林，靳晓光，陈绍清，王 琳

(1.重庆大学 土木工程学院，重庆 400030;2.重庆大学 山地城镇建设与新技术教育部重点实验室，重庆 400045;3.河北省区域地质矿产调查研究所，河北廊坊 065000;4.重庆科技学院 安全工程学院，重庆 401331)

0 引言

生产过程中在初期坝坝顶以上用尾矿充填堆筑而成的坝称为堆积坝，也叫后期坝。大、中型尾矿库堆积坝最终的高度往往比初期坝高的多，是尾矿坝的主体部分。堆积坝一旦失稳，灾害惨重，如何确保堆积坝的安全历来是设计和生产部门十分重视的一项工作，也是安全生产管理和安全监督管理工作的重点之一。因此，研究尾矿库堆积坝的稳定性具有重要的意义。

尾矿库堆积坝的筑坝方式有上游式、中线式、下游式和浓缩锥式等类型。吴家沟铝土矿尾矿库属于三面环山的山谷型尾矿库，堆积坝方式为上游式。尾矿库等别由各时期占用库容和坝高参数确定。当堆积达到库容100×104m3≤V＜1000×104m3、坝高30m≤H＜60m时，最高等别为四等尾矿库。在修筑好初期坝并完成前期库容堆填后，后续子坝采用碾压赤泥进行堆积，不断提升后期堆积高度，形成新的储矿区域。吴家沟尾矿库目前处于前期运行阶段，堆积坝每级子坝高度设计为6m，后一级子坝相对于前一级子坝向上游方向推移约15m，规划使用8～9级子坝后进行封坝，待前期尾矿库容中的赤泥进行一定排水固结后再修筑各级子坝。为了使库中赤泥颗粒分布较为均匀，采取在坝上多点放矿的方式。

极限平衡法和数值分析法是尾矿库坝体稳定性研究的主要方法。极限平衡法是最经典的边坡稳定性分析方法，在工程实践中使用最为广泛，也最为成熟。于斯滢、邵龙潭等［1］采用基于弹塑性应力应变分析的有限元极限平衡法对尾矿坝坝体的稳定性进行了研究;王启耀、何仕朝等［2］采用极限平衡法和快速拉格朗日法计算了御驾泉尾矿坝坝体在正常运行、洪水运行和特殊运行工况下的稳定系数;王立彬、袁子有等［3］采用Fellenius法、简化Bishop法和Janbu法对某尾矿坝坝体稳定性进行了计算。

数值分析法在尾矿库稳定性分析中已占有相当重要的位置，成为使用较为普遍的方法之一［4-5］。楼建东等［6］采用有限单元法对各种变量状况下尾矿坝坝体的应力和应变分布规律进行了研究，得出坝体内部潜在的滑动面;魏宁等［7］结合尾矿坝软基处理实践，运用Bioti固结有限元分析方法对尾矿库初期坝(土石坝)进行了数值模拟和预测，分析了固结过程中地基孔隙水压力和位移随时间的变化规律。Duncan(l996)［8］指出边坡安全系数可以定义为使边坡刚好达到临界破坏状态时对土的剪切强度进行折减的程度，即土的实际剪切强度与临界破坏时折减后的剪切强度的比值。随着计算机的发展和有限元计算技术的提高，有限元强度折减法正成为边坡稳定分析研究的新趋势。Dawson 和 Roth(1999)［9］，Manzari定边坡内所有土体的抗剪强度发挥程度相同时，抗剪强度折减系数可定义为边坡的整体稳定性安全系数，这样所确定的安全系数与使用极限平衡法计算得到的安全系数具有相同的概念。

按照上述的理解，坝体的安全系数就是把材料强度的特征值人为降低至堆积坝刚好出现临界破坏状态时刻的强度时所需要的折减系数，强度指标按下式进行折减［20］:

通过对材料的强度指标c，φ值进行不断调整，然后对研究对象采用有限元方法进行分析，使之不断接近临界状态而发生破坏，这时所获得的折减系数就是计算所需要的安全系数。对结果进行后处理能够比较直观地得到滑动面的位置。在整个模拟过程中不需要事先对滑动面位置做出假设，同时可以分析坡体破坏的整个发展过程和变形特点。

2.2 屈服准则的选取

影响边坡失稳破坏的关键因素是岩土体的抗剪强度，当最大剪应力达到破坏极限时，土坡将失稳破坏［21］。基于此，在应用折减系数法分析边坡稳定性时，采用理想弹塑性模型，屈服准则采用 Mohr-Coulomb破坏准则:

Mohr-Coulomb准则在实际工程中有较广泛的应用，不足之处在于其屈服面在三维应力空间中存在尖角状不连续点。在ABAQUS软件中通过运用扩展的Mohr-Coulomb准则，使得偏应力空间中不出现拐角，流动势呈现完全光滑的状态，塑性流动方向存在唯一性。

2.3 模型的建立及参数选取

根据尾矿库设计资料，参照尾矿坝纵断面图(图2)建立有限元分析模型。模型边界条件为:在基岩的左、右两侧设置水平向位移约束(U1=0)，基岩底侧设置水平向和竖直向位移约束(U1=U2=0)。模型采用四边形单元和三角形单元作为有限元分析的单元形式，二维有限元网格剖分共分为2737个单元，8522个节点。采用的物理力学参数如表2所列。

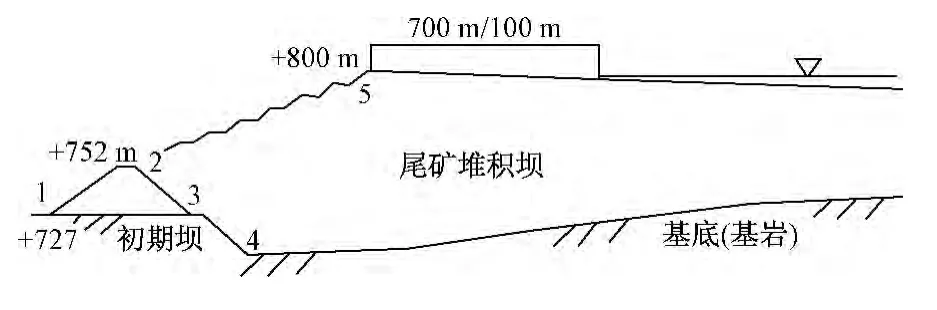
图2 尾矿坝纵断面示意图Fig.2 Longitudinal section diagram of tailings dam

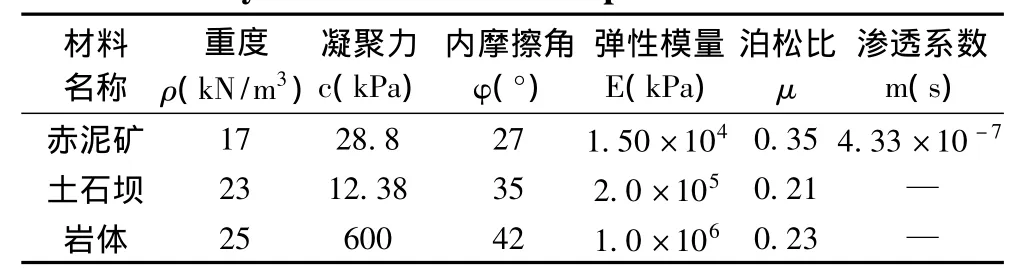
表2 材料物理力学参数Table 2 Physical and mechanical parameters of materials

2.4 尾矿库坝体稳定性分析

强度折减法的失稳判据包括迭代求解的不收敛性、特征部位位移的突变性、土体塑性应变和应力水平等某些物理量的变化和分布等。选取坡面某些特征位置发生突变的情况作为判定边坡失稳的依据能够有效地反映破坏变形过程，具有明晰的物理意义。采用对坡面顶点、子坝坡脚处的水平及竖向位移作为观察控制点，分析其与折减系数之间的关系，将塑性区的发展变化作为失稳破坏的补充判据。通过强度折减的方式获得坡体的安全系数。在选取坝体的初始强度时，给予适当的加大，取强度折减系数Fs=0.8(即加大尾矿坝稳定性)，逐渐增大Fs值，当其值增加到1以后，即开始减小土体的抗剪强度参数值c和tanφ，运用ABAQUS进行计算获得相应的位移场和应力场分布特征。折减系数以0.1的增幅逐渐提高，得到随折减系数增大而不断变化的位移场和应力场。通过分析坡顶和坡脚两处控制点的水平及竖向位移与强度折减系数的变化趋势，获得相应节点的位移与强度折减系数Fs的关系曲线如图3和图4所示。

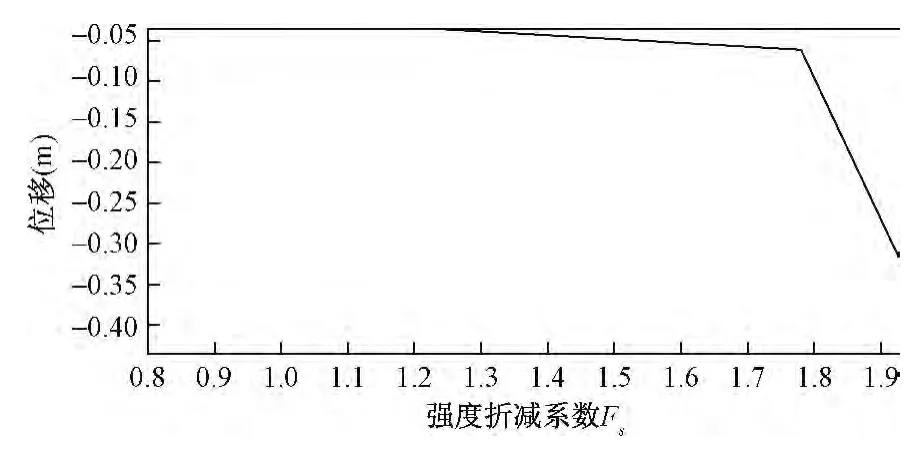
图3 堆积坝坡脚水平位移U1与折减系数关系曲线Fig.3 Relation curve of Horizontal displacement on slope toe and reduction factor

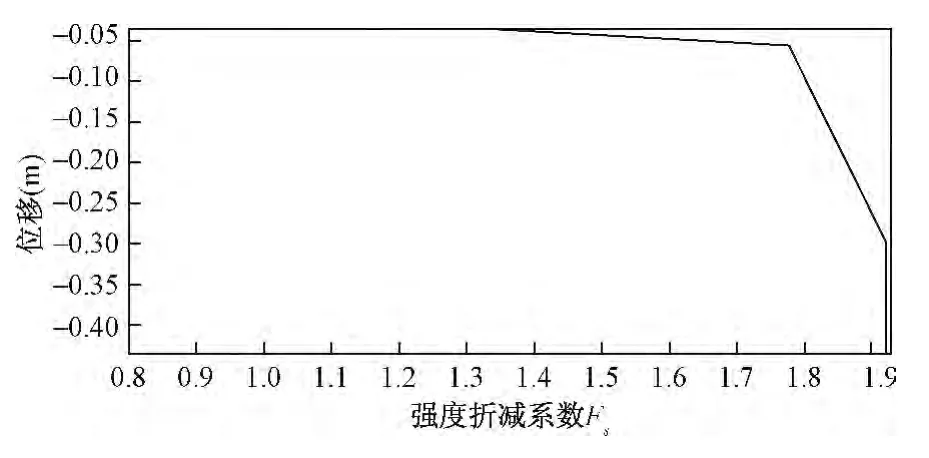
图4 堆积坝顶竖向位移U2与折减系数关系曲线Fig.4 Relation curve of vertical displacement on dam crest and reduction factor

由图3和图4可以看出，当强度折减系数Fs小于1.76之前，坡顶、坡脚两处位移随Fs的提高而缓慢增加，基本上显示为水平直线发展，表明节点位移对于抗剪强度的减小发生的改变并不明显，当折减系数Fs从0.8增加至1.76的过程中，边坡状态一直保持相对稳定。当Fs达到1.76以后，两处位移值随着强度折减系数Fs的增加发生了比较明显的增大过程，位移值出现拐点。在后期急剧增加，出现垂直增长阶段，表明当边坡土体强度指标折减至1.76后，两处位移值随着土体强度的降低出现快速的增长。此时在边坡土体内部的塑性应变区域开始迅速发展，并自坡脚延伸到坡顶逐渐贯通呈带状分布，处于带状区域范围的土体强度接近极限状态(图8)。边坡自重作用引起的下滑力与土体所具有的抗剪强度提供的抗滑力相等，继而发生滑动破坏。可以认为，有限元强度折减法得到的堆积坝边坡安全系数为1.76，与极限平衡分析所获得的安全系数值K=1.73非常接近，说明采用强度折减法的位移突变准则确定边坡稳定的安全系数是可行的。

计算中不同增量步时间点t对应的塑性区分布如图5～图8所示，分析坝体内塑性区的变化过程可以说明尾矿库堆积坝体的破坏过程。

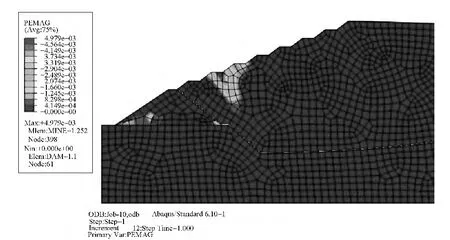
图5 未进行强度折减(step－1)的塑性区分布Fig.5 The plastic zone distribution without strength reduction

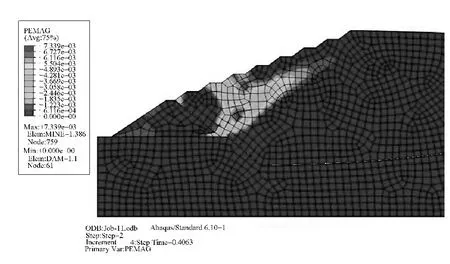
图6 强度折减(step－2)t=0.4063的塑性区分布Fig.6 The plastic zone distribution with strength reduction at time=0.4063

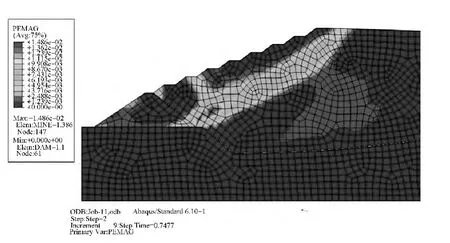
图7 强度折减(step－2)t=0.7477的塑性区分布Fig.7 The plastic zone distribution with strength reduction at time=0.7477

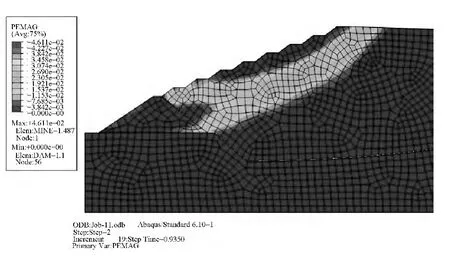
图8 强度折减(step－2)t=0.935的塑性区分布Fig.8 The plastic zone distribution with strength reduction at time=0.935

图5为不进行强度折减时的塑性区分布，在2～3级子坝出现了少量塑性变形，最大值为4.97×10-3，面积分布为559.41m2。图6～图8分别为进入强度折减的第二个分析步过程中 t=0.4063、t=0.7477和t=0.935的PEMAG(积分点上的等效塑性应变)分布。随着坝体强度参数的减小，塑性变形向内部发展，在t=0.4063时，塑性区域深入坡面大约29m，并沿着与水平位置呈约32°的方向往初期坝的坝踵(点3)和堆积坝的坝顶(点5)方向延伸(图2)，最大点位于初期坝坝踵附近，为7.33×10-3，塑性区面积增大到1706.61m2;在t=0.7477时，塑性区分布已经延伸至堆积坝顶面，最大值为1.48×10-2，分布面积2255.57m2;随着强度指标的进一步下降，在t=0.935时，塑性区域向初期坝顶发展，最大值出现在堆积坝下游坡面的坡脚处(点2)，达4.61×10-2，分布面积达到2479.71m2，塑性区在向下游延伸过程出现分叉状态，分别向初期坝坝顶和坝底延伸，引起初期坝的位移与变形，使坝体内抗剪强度得以发挥，静止土压力过渡为主动土压力，初期坝的支挡作用阻止了堆积坝的滑动破坏，此时的位移计算仍然收敛。但随着强度指标的继续下降，堆积坝坡面形成贯通的塑性区，通过初期坝顶(点2)和堆积坝的坝顶(点5)，位移迅速增长，最终发生滑面失稳破坏。

在堆积坝的有限元分析中，强度折减后计算得到的位移等值线图能够直观地反映堆积坝滑动面的特征(图9)。通过图9可以较容易地判断堆积坝滑动面的位置，此时坡顶出现位移最大值，为2.49m，说明坝体已出现滑动破坏。滑动面形状与极限平衡法分析结果比较一致，呈大致的圆弧状，通过堆积坝坡脚(点2)。从坝体整个破坏过程看出，坡体内没有出现沿点3至点5的贯通滑移面主要是依靠初期坝的作用。

3 结论和建议

(1)采用极限平衡条分法计算得到吴家沟尾矿库堆积坝的安全系数为1.73，滑动面形状为圆弧形。

(2)应用ABAQUS软件，采用有限元强度折减法得到堆积坝的安全系数为1.76，与极限平衡分析法得到的堆积坝安全系数基本一致。

(3)极限平衡法和有限元强度折减法的有机结合是分析土质堆积坝稳定性比较有效的方法。

图9 强度折减(step－2)后位移等值线图Fig.9 The displacement contour with strength reduction

(4)在堆积坝安全控制方面，合适的堆积坝坡度和尾矿堆积体的强度指标是非常重要的因素。

［1］于斯滢，邵龙潭，刘士乙.基于有限元极限平衡法的尾矿坝坝体稳定分析［J］.岩土力学，2012，34(4):1185-1190.YU Siying，SHAO Longtan，LIU Shiyi.Stability analysis of tailings dam based on finite element limit equilibrium method［J］.Rock and Soil Mechanics，2012，34(4):1185-1190.

［2］王启耀，何仕朝，谢孔金.御驾泉尾矿坝稳定性计算与分析［J］.金属矿山，2012(1):55-57.WANG Qiyao， HE Shichao， XIE Kongjin.Stability calculation and analysis of the Yujiaquan tailing dam［J］.Metal Mine，2012(1):55-57.

［3］王立彬，袁子有，侯攀，等.某尾矿坝边坡稳定性计算与安全分析［J］.有色金属(矿山部分)，2012，63(5):52-56.WANG Libin，YUAN Ziyou，HOU Pan，et al.Slope stability calculation and safety analysis of a tailings dam［J］.Nonferrous Metals(Mining Section)，2012，63(5):52-56.

［4］Enoki，Meiketsu，Yagi，Norio et al.Relation of limit equilibrium method to limit analysis method［J］.Soils and Foundations，1991，31(4):37-47.

［5］Nemirovskii，Yu.V.，Nalimov，A.V.A method for solving problems on the limit equilibrium of reinforced shells ofrevolution［J］. Mechanics ofComposite Materials，2008，44(5):427-440.

［6］楼建东，李庆耀，陈 宝.某尾矿坝数值模拟与稳定性分析［J］. 湖南科技大学学报，2005，20(2):58-61.LOU Jiandong，LI Qingyao，CHEN Bao.Tailing-dam math simulation and stability analysis［J］.Journal of Hunan University of Science＆ Technology(Natural Science Edition)，2005，20(2):58-61.

［7］魏宁，茜平一，张波，等.软基处理工程的有限元数值模拟［J］.岩石力学与工程学报，2005，24(2):5789-5794.WEI Ning，QIAN Pingyi，ZHANG Bo，et al.Simulation of treatment of soft clay foundation by fem method［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24(2):5789-5794.

［8］Dunean J M.State of the art:Limit equilibrium and finite-elementanalysis ofslopes ［J］. Journalof Geotechnical Engineering，AS-CE，1996，122(7):577-596.

［9］Dawson E M，Roth W H，Dreseher A.Slope stability analysis by stress reductio ［J］.Geotechnique，1999，49(6):835-840

［10］Manzari M T，Nour M A.Significance of soil dilatancy in slope stability analysis［J］.Journal of Geotechnical and Geoenviron-mental Engineering，ASCE，2000，126(1):75-80.

［11］宋二样.土工结构安全系数的有限元计算［J］岩土工程学报，1997，19(2):1-7.SONG Erxiang.Finite element analysis of safety factor for soil structures［J］.Chinese Journal of Geotechnical Engineering，1997，19(2):1-7.

［12］赵尚毅，郑颖人，时卫民，等.用有限元强度折减法求边坡稳定安全系数［J］.岩土工程学报，2002，24(3):343-346.ZHAO Shang yi，ZHENG Ying ren，SHI Wei min，et al.Analysis on safety factor of slope by strength reduction FEM［J］.Chinese Journal of Geotechnical Engineering，2002，24(3):343-346.

［13］张鲁渝，郑颖人，赵尚毅，等.有限元强度折减系数法计算土坡稳定安全系数的精度研究［J］.水利学报，2003(1):21-27.ZHANG Luyu，ZHENG Yingren，ZHAO Shangyi，et al.The feasibility study of strength-reduction method with FEM for calculating safety factors of soil slope stability［J］.Journal of Hydraulic Engineering，2003(1):21-27.

［14］郑颖人，赵尚毅，张鲁渝.用有限元强度折减法进行边坡稳定分析［J］.中国工程科学，2002，4(10):57-78.ZHENG Yingren，ZHAO Shangyi，ZHANG Luyu.Slope stability analysis by strength reduction FEM ［J］.Engineering Science，2002，4(10):57-78.

［15］郑颖人.岩土数值极限分析方法的发展与应用［J］.岩石力学与工程学报，2012，31(7):1297-1313.ZHENG Yingren. Developmentand application of numerical limit analysis for geological materials［J］.Chinese Journal of Rock Mechanics and Engineering，2012，31(7):1297-1313.

［16］陈昌富，翁敬良.基于广义Hoek-Brown准则边坡稳定性分析强度折减法［J］.中国地质灾害与防治学报，2010，21(1):13-17.CHEN Changfu，WENG Jingliang.Strength reduction method based on generalized Hoek-Brown criterion for slope stability analysis［J］.The Chinese Journal of Geological Hazard and Control，2010，21(1):13-17.

［17］李红卫，马惠民，张忠平.强度折减法在高含水滑坡稳定性分析中的应用［J］.中国地质灾害与防治学报，2009，20(3):27-30.LI Hongwei， MA Huimin， ZHANG Zhongping.Application of strength reduction method in stability analysis of a landslide with high water content［J］.The Chinese Journal of Geological Hazard and Control，2009，20(3):27-30.

［18］李宁，许建聪.基于场变量的边坡稳定分析有限元强度折减法［J］. 岩土力学，2012，33(1):314-317.LI Ning，XU Jiancong.Strength reduction FEM for slope stability analysis based on field variable［J］.Rock and Soil Mechanics，2012，33(1):314-317.

［19］陈力华，靳晓光.有限元强度折减法中边坡三种失效判据的适用性研究［J］.土木工程学报，2012，45(9):136-145.CHEN Lihua，JIN Xiaoguang.Study on the applicability of three criteria for slope instability using finite element strength reduction method［J］.China Civil Engineering Journal，2012，45(9):136-145.

［20］连镇营，韩国城，孔宪京.强度折减有限元法研究开挖边坡的稳定性［J］.岩土工程学报，2001，23(4):407-411.LIAN Zhen ying，HAN Guo cheng，KONG Xian jing.Stability analysis of excavation by strength reduction FEM［J］.Chinese Journal of Geotechnical Engineering，2001，23(4):407-411.

［21］徐干成，郑颖人.岩土工程中屈服准则应用的研究［J］. 岩土工程学报，1990，12(2):93-99.XU Gancheng，ZHENG Yingren.Study on the yield criterion applied in geotechnical engineering［J］.Chinese Journal of Geotechnical Engineering，1990，12(2):93-99.