三峡库区陡岩滑坡涌浪爬高试验分析

杨渠锋，王平义，2，喻 涛，2，陈 里

(1.重庆交通大学 河海学院，重庆 400074;2.国家内河航道整治工程技术研究中心，重庆 400074)

0 引言

波浪爬高是指波浪在堤坝上上爬高度与静水面之间的垂直距离。波浪爬高是确定水工建筑物堤顶高程的重要指标之一，直接关系到堤坝及岸上建筑物的安全。水库崩滑体失稳后会发生滑坡，岩土体急剧进入水体中，形成具有灾害性的滑坡涌浪。涌浪以岩土体入水处为起始点，沿河道上下游传播，对航道沿岸基础设施和居民地造成严重威胁［1-2］。

目前，国内外关于地质灾害类波浪爬高方面的研究主要是基于现场观测分析、试验模型及数值模拟分析。其中国内的数值模拟研究方法起步较晚且大都采用N-S方程的k-ε湍流模型和VOF方法，以源函数造波进行湍流数值模拟，建立了能够造波、消波的数值波浪水槽，较好的模拟了波浪爬高及越浪过程［3-6］。周丰［7］等则运用加入了亚格子湍流模式的Poisson方程去迭代求解压力场的SPH方法，建立了不可压缩流体运动的PSPH数学模型，该模型更加精确地描述了波浪破碎时的湍流特性，模型模拟了椭圆余弦波在斜坡上的爬坡过程，并与试验结果对比分析，吻合较好。

在模型试验方面，刘宙［8］分析了波浪在堤坡面上的破碎形态，首次考虑了波浪斜向入射角度对爬高的影响，提出对斜向波浪爬高的研究可采用等效坡度这个概念。李建习［9］等从坝体护面结构和堤前植物带分析它们对波浪爬高的影响，并应用国内外主流的爬高计算公式进行实例对比分析，发现各家公式计算结果差异较大。汪洋［10］结合明渠非恒定流与水动力学，提出了滑坡涌浪从入水点的衰减规律，考虑斜坡坡脚和爬坡方位角，据此得到了涌浪沿岸的爬高公式。郑殿祥，周荣星［11］等对平原水库坝高设计中波浪爬高进行了计算对比分析，认为蒲田公式更加适用于平原水库的设计。陈国平，王铮［12］等通过物理模型试验，研究了不规则波作用下不透水单坡上的波浪爬高，得到了海堤结构波浪爬高的计算公式及其不同频率累积换算关系。2002年，荷兰的防洪咨询委员会［13］(TAW)针对海堤和河堤的评估设计，采用谱波参数分析法对波浪爬高和越浪量的计算进行了详细的分析研究。M.Di Risio，P.De Girolam及 G.Bellotti［14］在模型试验中采用半椭圆形的刚性滑坡体，研究了圆形岸边滑坡所激起的涌浪浪高，详细分析了初始涌浪高度的动态传播规律及涌浪爬坡的特点。试验结果表明，涌浪浪高在发生点附近高度增大，在滑坡宽度两倍范围之外开始衰减。圆形海岸半径越大，涌浪爬坡高度越大。不难看出，之前对涌浪爬高的研究绝大部分都是关于海洋堤防和平原水库的，对于山区水库陡岩滑坡涌浪爬高的研究非常少。

三峡库区陡岩滑坡主要由崩塌、危岩和落石组成，由于受地质岩性和构造、河谷地形地貌、岸坡结构类型和人类活动等影响，三峡库区陡岩滑坡分布呈明显的地带性。根据统计资料显示，三峡库区约90%的陡岩都发育在具有软弱夹层的侏罗系和三叠系中上统层状岩层中，坚硬的岩层下伏有软弱层时易发生崩塌［15］。陡岩滑坡滑速大，入水时溅起的高度大，可预测性低，尽管其滑坡体规模往往较土石滑坡小，但危害性不可忽视。近些年我国西南地区水利水电工程的快速发展，伴随着库区水位的急剧变化，已有的和潜在的陡岩滑坡对整个库区及下游人民的安全都构成了巨大的威胁，所以，关于陡岩滑坡涌浪爬高的研究迫在眉睫。

本次模型试验选取三峡库区典型的陡岩滑坡作为研究对象，考虑了坡前波陡、坡前相对波高和斜坡坡度等主要因素，得出适合于陡岩滑坡的初始涌浪爬高计算公式，为库区护岸整治工程和港口码头的坝顶高程设计及陡岩滑坡灾害预报提供了一定的参考价值。

1 试验模型布置及测量仪器

1.1 模型布置

模型模拟河段采用万州江南沱口码头段，该河段上起航道里程336km，下至航道里程330km，长约6km。根据实测的河段地形图(图1)，明显看出试验段为弯曲河段且弯曲角度大致为90°，确定将试验河段概化成90°弯曲型的河道(图2)，并采用清水定床模型。模型采用断面法制作并对河底地形进行概化，从试验河段地形图中提取出每个断面的数据，绘制成图，且对弯道段和直道段地形数据分别统计。统计结果显示:弯道段地形变化逐渐过渡，直道段变化不大。于是，试验拟将断面概化成弯道段和直道段，弯道段概化成90°，相邻两个断面间隔3°，每个断面的参数取该断面附近统计值的均值;直道段长度和坡度取统计值的均值。

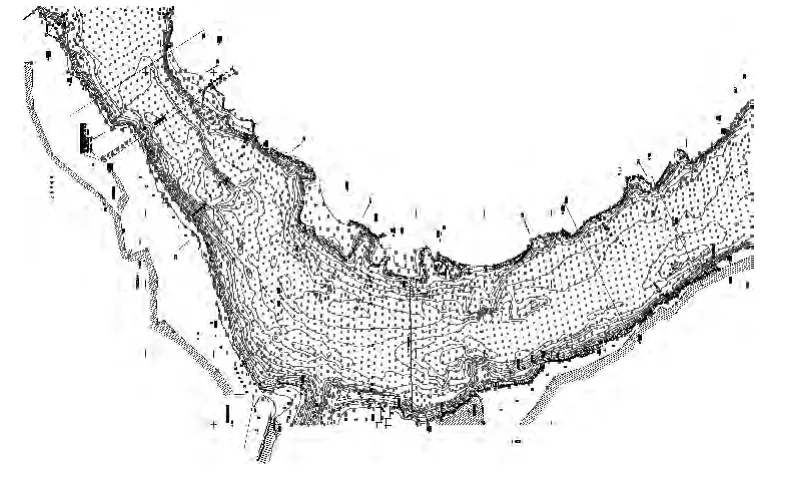
图1 河段地形图Fig.1 Reach topographic map

图2 概化段平面图(单位:m)Fig.2 Generalized section plan(Unit:m)

三峡水库运行的水位有正常蓄水位145m、汛期防洪限制水位155m、枯水期消落水位175m，河道概化段的底部平均高程是93.55m，模型按照1∶70的比尺进行设计，概化河道模型总长52m，宽8m，试验水深依次为:0.74m、0.88m、1.16m三个水平。

根据收集的三峡库区典型陡岩滑坡统计资料，60°～90°的陡峻边坡最易发生陡岩滑坡，60°以下边坡出现崩落概率较小。所以，试验滑坡坡度分别选取60°、70°、80°和 90°。滑坡块体采用细砂、石子和水泥来制作大小不同的密度相似的矩形滑坡块体，并按不同的组合方式堆放滑坡体，以此来模拟陡岩滑坡体的裂隙发育程度。考虑以上三个因素:水深、坡度和块体大小，并结合单因素方差分析方法，试验共设置了72组方案，其中，本文选取了试验结果较为完整的55组方案。

滑槽采用木质材料制作:槽底部选用表面粗糙的厚木板，以达到整体强度及滑面阻力要求。对需要考虑地形起伏度的方案，可将试验前期制作好的三角形长木条固定在滑槽底部(图3)，使得滑坡体在下滑过程中与滑面发生碰撞，并产生跳跃和翻滚等切合实际的运动轨迹;滑槽两内壁选用较光滑的木料，且在其表面上铺订铁皮以减小摩阻力，降低滑坡体的能量损耗。

图3 滑槽起伏度Fig.3 Slideway Waviness

1.2 测量仪器与测量方法

波高的测量采用重庆交通大学西南水运工程科学研究所自主研发的UBL-2超声波浪采集分析仪，频率为25HZ。测点分为8个测量断面，共16个测点(图4)。靠近入水点的三只传感器测量初始涌浪，其余13只传感器测量沿程涌浪。为了不影响涌浪形态并保护仪器，确定这三只传感器距离入水点0.5m。

图4 模型及浪高测点平面布置图(单位:m)Fig.4 Model and wave measuring point layout(Unit:m)

波高的测点布置基于点击波理论，采用圆形的布置方案，测量同一圆弧上多个点的波高均值作为这一半径上波浪的波高值，外围测点用于测量沿程涌浪，沿程涌浪传播的测定方式为两点法。

爬高测点共4个，分布在滑坡入水点的邻岸、对岸、对岸弯道处、模型弯道最远端，对应测点号为1#、2#、3#和4#(图5)。每个测点表面固定有精度为±0.1mm的米尺，在米尺上洒一层平均粒径为0.06mm的薄粉沙，通过试验前后被涌浪冲落薄粉沙区域下边界对应米尺的读数差值，结合测点斜坡面的坡度计算出该测点涌浪的爬高。

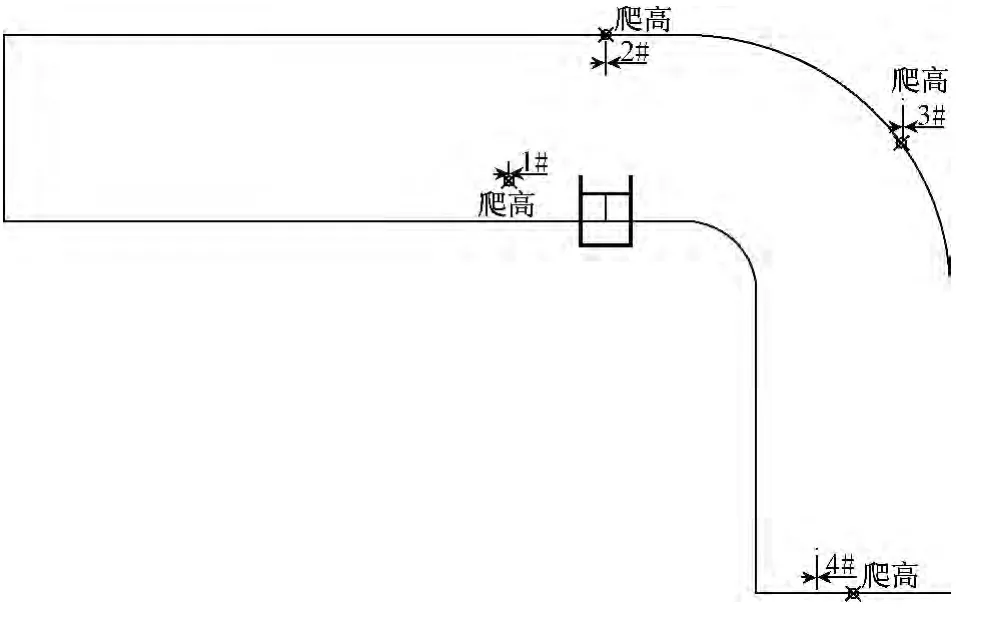
图5 涌浪爬高测点Fig.5 Climb measuring point

1.3 测量数据分析

初始涌浪波高作为判别滑坡灾害的一项初始依据，对灾害预报具有重要的参考意义。试验测得的最大初始涌浪高度为8.47cm，由试验比尺，反算出原型的最大波高为5.93m;最小初始涌浪高度为1.87cm，反算出原型的最小波高为1.31m;模型涌浪平均波高为4.39cm，反算出原型的平均波高为3.07m。对试验初始波高的观测可知，在同一方案中，靠近入水点50cm处的三只波高仪测得的波高最大，且其最大波高基本相同。随着传播距离的增加，波高有明显的衰减，同一圆弧上的涌浪波高大致相等，这与圆弧波理论一致。

波陡是波高与波长之比，它表征了波动的平均斜率。在有限振幅波理论中，波陡的极限值为0.142，大于该极限值时，波面会发生破碎。选取本次试验不同方案下不同测点的153组统计值，有2组数据超过了极限波陡，其值分别为0.152、0.156，其余各工况下，波陡值均小于极限值，这与工程经验值基本一致，证明了试验结果的可靠性。

提取55组工况下测得的爬高数据并计算其均值及原型均值(表1)。由表1可知，1#测点附近的最大值和均值都是最大的，说明1#测点附近处于最危险的区域。

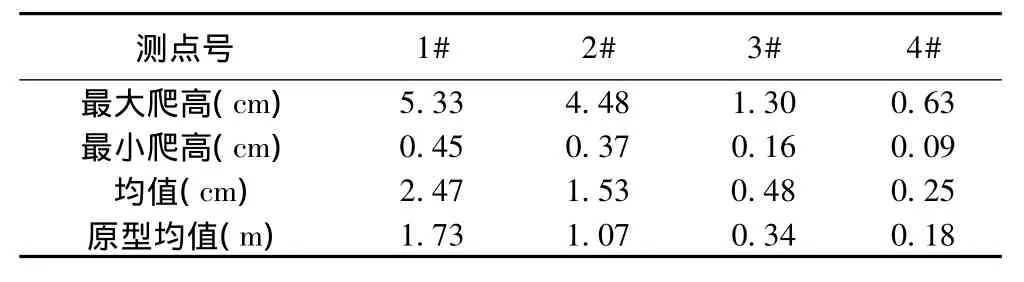
表1 爬高测量表Table 1 Climb measurements

2 滑坡涌浪在河道中的传播

涌浪属于自由波，呈现出较为规则的波峰和波谷，其波形接近于简谐波。滑坡体高速滑入模型水库中激起波浪，同时近水面急剧升高，形成初始涌浪并迅速向外传播。由于涌浪内部能量损耗和摩阻力的影响，波高在短时间内迅速衰减到一定程度后，随着传播距离的增加和波浪非对称性的减弱，衰减程度越来越缓慢，涌浪也趋于规则，当涌浪传播至坡面时，由于坡面的阻挡，涌浪的总能量最终消耗在坡岸上并形成涌浪在此坡面处的爬高。

从涌浪“触底”时起，涌浪便开始损失能量，涌浪的波高随之开始衰减。引起波高的衰减的原因一般有包括三个方面:摩阻损失、渗透损失和泥面波阻力损失［16］。根据实验条件和之前学者研究发现，后两种损失并不显著可不予考虑。而底部摩阻引起的波高衰减是由于非理想水体近底部边界层的粘性能量耗散引起的，由底部摩阻引起的波高衰减可根据波能流连续方程导出，得出波高衰减关系式:

通过对比分析，选取试验结果较为完整的10个测点的初始沿程涌浪浪高并计算出这10个测点初始沿程涌浪的波高衰减系数(初始涌浪传播到某点时的波高Hx与该方案下初始涌浪波高H0的比值即为初始涌浪传播到该点的波高衰减系数)，结合涌浪传播距离发现，涌浪从入水点传播到3m处时的波高衰减变化程度明显较涌浪传播到5.5m、9.5m甚至更远距离的波高衰减剧烈。所以，根据公式(1)并综合试验涌浪性质，本文将涌浪传播的波高衰减系数分为两个阶段来考虑，即以涌浪传播到3m时和从3m传播到河对岸的两个阶段，暂且认为是第一阶段和第二阶段。

用无量纲方法来探讨波高衰减系数K与相对波高H0/h、相对传播距离L/h之间的关系。本文分别采用线性函数、指数函数进行线性回归分析，得到如下4个波高衰减系数计算的经验公式:

第一阶段:

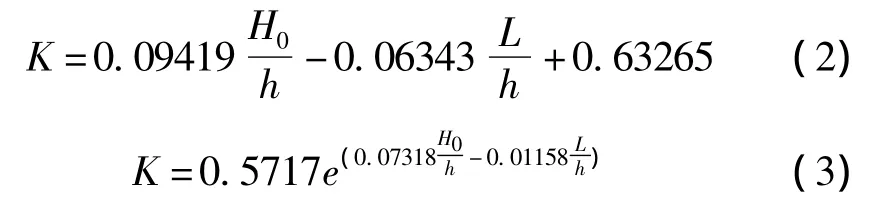
第二阶段:

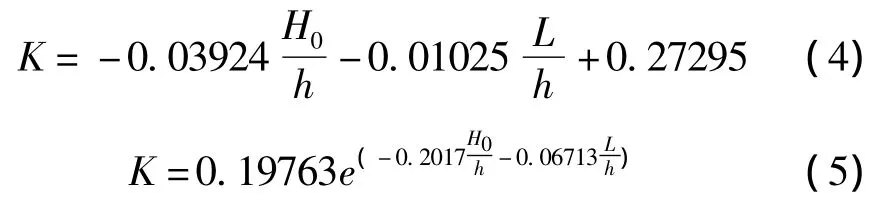
利用上述四个公式计算所选工况下波高衰减系数的计算值并与试验值进行对比，结合y=x趋势线将结果绘制成图(见图6、7、8、9)，从对比图中看出:公式(3)计算值与试验值较公式(2)吻合，公式(5)计算值与试验值较公式(4)吻合，且从表2也可以看出公式(3)和公式(5)的平均相对误差和离差平方和较小，因此，建议采用公式(3)和公式(5)计算涌浪传播的衰减系数。

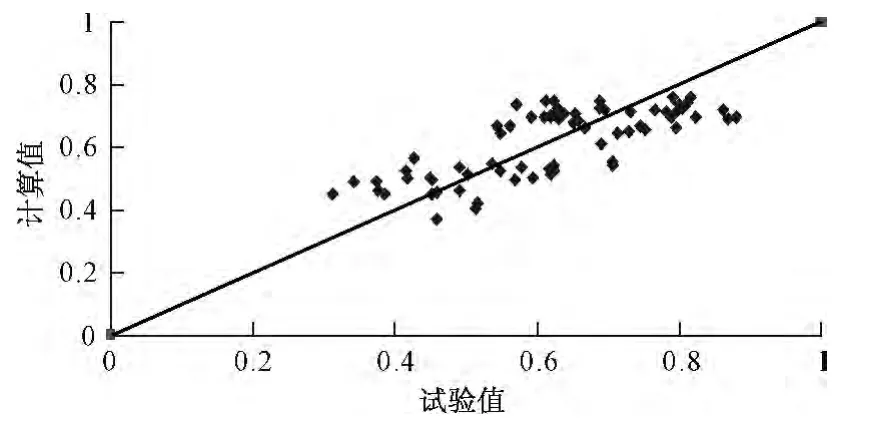
图6 公式(2)计算值与试验值对比图Fig.6 Calculated value and measured value of equation(2)

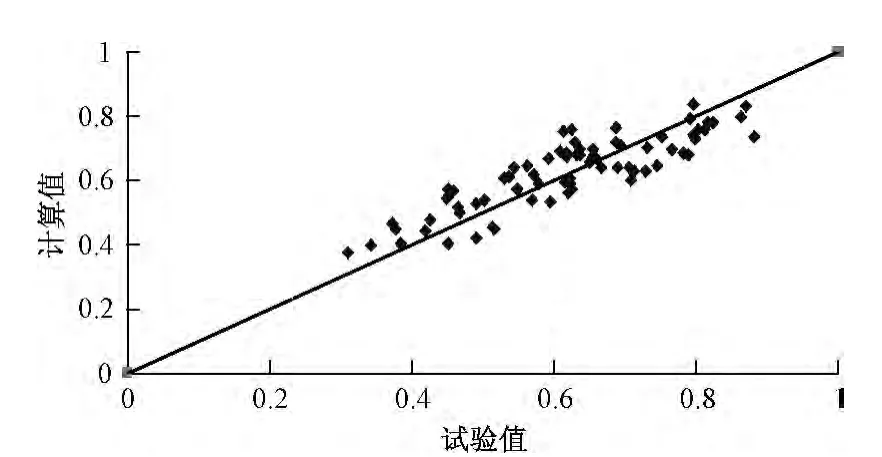
图7 公式(3)计算值与试验值对比图Fig.7 Calculated value and measured value of equation(3)

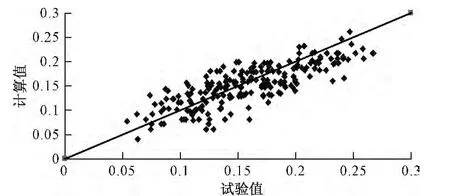
图8 公式(4)计算值与试验值对比图Fig.8 Calculated value and measured value of equation(4)

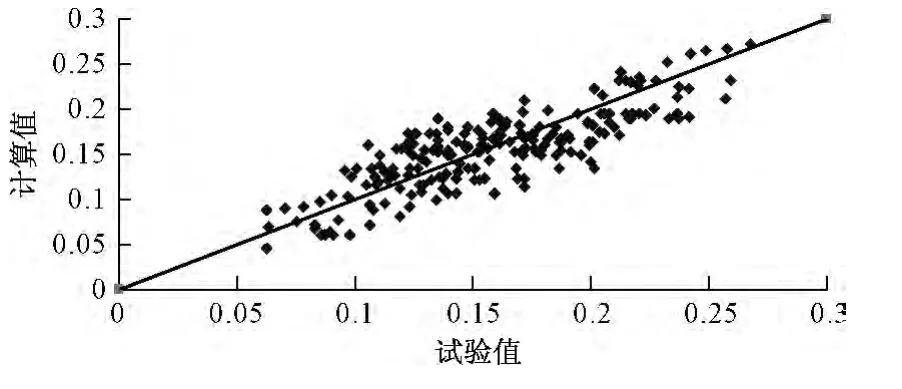
图9 公式(5)计算值与试验值对比图Fig.9 Calculated value and measured value of equation(5)

3 滑坡涌浪爬高分析

试验模型共设置了4个坡面爬高测点。其中，1#、2#和3#测点距滑坡入水点的水平直线距离，就是初始波传递到爬坡测点的传播距离。由于4#测点布置在弯道另一侧的河岸，当波浪传播到4#测点要经过先弯道。所以，4#测点的传播距离除了水平直线距离外，还要再加上波浪绕弯所经过的水平圆弧距离。根据概化模型资料和试验水深，经计算可得各测点在不同试验水深下的涌浪传播距离(表3)。

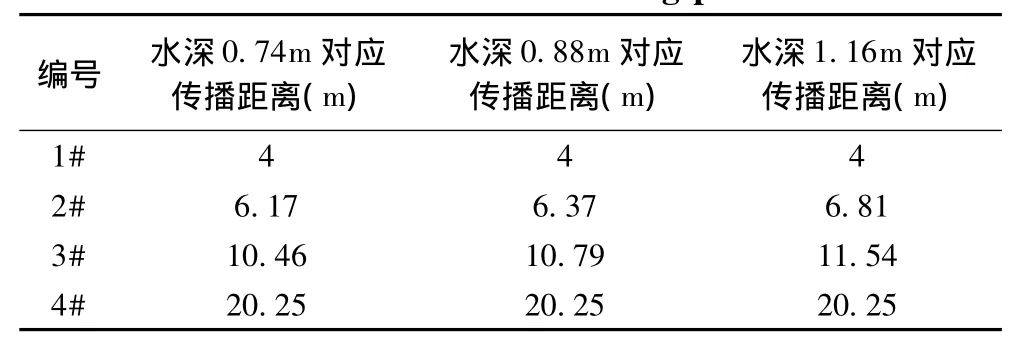
表3 爬高测点Table 3 Climb measuring point

涌浪爬高是设计堤顶高程的一个重要参数，它直接影响堤坝结构的稳定性。涌浪爬高的影响因素非常复杂，我国交通运输部《海港水文规范》中，关于正向规则波在斜坡式建筑物上的波浪爬高公式为:

与波陡H/L(L为坡前波长)、坡前相对波高H/d(d为水深)及斜坡坡度α(α为弧度制)等有关。则上述公式可以转换为:

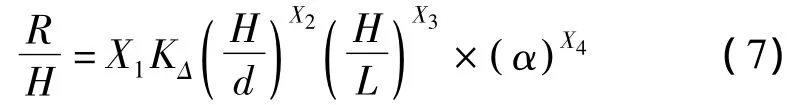
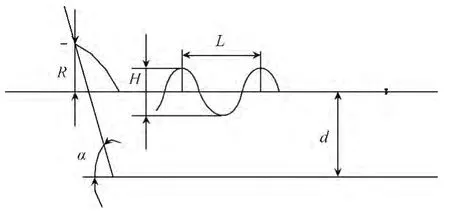
图10 斜坡上的涌浪爬高Fig.10 Climb on the slopes swell

本次试验涌浪周期T的读取采用跨零点法，测得的周期T范围约为0.37～1.02s，根据试验模型比尺，其原型周期范围约为3.1～8.55s。试验涌浪符合有限振幅波理论，采用斯托克斯波的二阶解计算波速c较合适，由深水情况下波速c的二阶解导出波长L的求解公式(8)，从而可计算出55个方案下各波的波长。

对于混凝土护面，粗糙系数 KΔ一般取值为0.9［17］，而坡前波高H可以通过初始波高及波高衰减公式求得。采用最小二乘法对式(7)的系数进行回归分析，得出陡岩滑坡涌浪的爬高计算公式(9)。

将试验资料与公式(9)计算结果进行对比，从对比图中看出公式(9)计算值稍微偏大一些，但总体来说，计算值与试验值吻合较好(图11)。

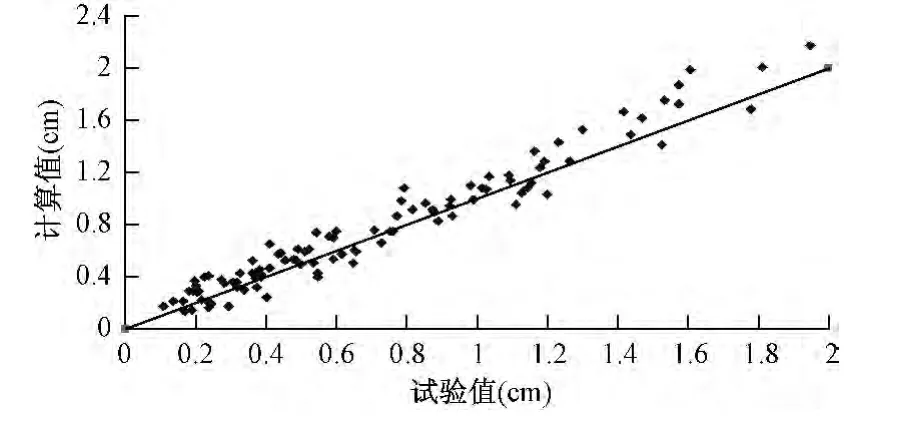
图11 公式(9)计算值与试验值对比图Fig.11 Calculated value and measured value of equation(9)

4 结语

本次试验选取三峡库区典型的陡岩滑坡作为研究对象，通过水槽概化模型试验，采用不同堆放组合下的矩形滑坡体，很好的模拟了陡岩滑坡发生、涌浪形成及传播的整个试验过程。

试验数据处理选择测量结果较为完整的55组波高数据，分析了初始涌浪高度沿河道传播的衰减规律，根据波高衰减变化程度把衰减系数计算分为从初始涌浪传播到3m时和从3m传播到河对岸两个阶段来考虑，运用多元线性回归分析方法得出了初始涌浪高度衰减系数的计算公式。据此，结合爬高试验测值和相关资料，得出了陡岩滑坡涌浪爬高的计算公式，其计算值与试验值拟合较好。

［1］黄波林，殷跃平.基于波浪理论的水库地质灾害涌浪数值分析方法［J］.水文地质工程地质，2012，39(4):92-97.HUANG Bolin，YIN Yueping.Method ofreservoir geohazard impulsive wave simulation based on wave theory［J］.Hydrogeoloy＆Engineering Geology，2012，39(4):92-97.

［2］邱昕，邢爱国，王国章.基于FLUENT数值模拟的滑坡涌浪分析［J］.中国地质灾害与防治学报，2013，24(3):26-31.QIU Xin，XING Aiguo，WANG Guozhang.Numerical simulation analysis of water waves due to landslide based on FLUENT［J］.The Chinese Journal of Geological Harzand and Control，2013，24(3):26-23.

［3］周勤俊，王本龙，兰雅梅，等.海堤越浪的数值模拟［J］.力学季刊，2005，26(4):629-633.ZHOU Qinjun， WANG Benlong， LAN Yamei， et al.Numerical simulation of wave overtopping over seawalls［J］.Chinese Quarterly of Mechanics，2005，26(4):629-633.

［4］杨锦凌，孙大鹏，吴浩，等.斜坡堤波浪爬高和越浪数值模拟［J］.海洋工程，2013，31(2):45-52.YANG Jinling，SUN Dapeng，WU Hao，et al.Numerical simulation of wave run-up and overtopping on sloping seawall［J］.The Ocean Engineering，2013，31(2):45-52.

［5］祁国军，袁新明.斜坡堤栅栏板护面波浪爬高数值模拟［J］.水利水电科技进展，2012，32(5):16-19.QI Guojun，YUAN Xinming.Numerical simulation of wave run-up on fence panels of sloping dikes［J］.Advances in Science and Technology of Water Resources，2012，32(5):16-19.

［6］杨锦凌.动量源方法模拟斜坡堤爬高和越浪［D］.辽宁:大连理工大学，2012.YANG Jinling.Numerical simulate runup and overtopping of slope dike base on momentum source［D］.Liaoning:Dalian University of Technology，2012.

［7］周丰，孙家文，郑坤.波浪爬高的PSPH方法数值模拟研究［J］.水运工程，2011(2):1-6.ZHOU Feng，SUN Jiawen，ZHENG Kun.PSPH method for simulating wave run-up on slope［J］.Port＆ Waterway Engineering，2011(2):1-6.

［8］刘宙.斜向波爬高的试验研究［J］.河海大 学报:自然科学版，1990，18(1):118-121.LIU Zhou.Oblique wave run-up experimental research［J］.Journal of Hohai University(Natural Sciences)，1990，18(1):118-121.

［9］李建习，沈小雄，赵利平，等.影响库区波浪爬高因素的分析［J］.水电能源科学，2007，25(5):95-98.LI Jianxi，SHEN Xiaoxiong，ZHAO Liping，et al.The analysis of the influence factors of reservoir wave run-up［J］.Water Resources and Power，2007，25(5):95-98.

［10］汪洋，殷坤龙.水库库岸滑坡涌浪的传播与爬高研究［J］.岩土力学，2008，29(4):1031-1034.WANG Yang，YIN Kunlong.Research on propagation and climb height of surge triggered by landslide in reservoir［J］.Rock and Soil Mechanics，2008，29(4):1031-1034.

［11］郑殿祥，周荣星，金瑞清，等.平原水库波浪爬高计算方法探讨［J］.人民黄河，2009(3):86-87.ZHENG Dianxiang，ZHOU Rongxing，JIN Ruiqing，et al.The discussion of the plain reservoir wave run-up calculation method ［J］.Yellow River， 2009(3):86-87.

［12］陈国平，王铮，袁文喜，等.不规则波作用下波浪爬高计算方法［J］.水运工程，2013(1):151-159.CHEN Guoping，WANG Zheng，YUAN Wenxi，et al.Calculation of wave run-up under the irregular wave action［J］.Port ＆ WaterwayEngineering， 2013(1):151-159.

［13］TAW.TechnicalReport:WaveRun-up and Wave Overtopping at Dikes，2002.

［14］M.DiRiso， P.DeGirolamo， G.Bellotti.2009，Landslide-generated tsunamis runup at the coast of a conical island:New Physical model experiments［J］.Journal of geophysical research，Vol.114，C01009.

［15］门永强.山区河道型水库陡岩滑坡涌特性及对航道通航条件影响研究［D］.重庆:重庆交通大学，2013.MEN Yongqiang.Experimental research on dangerous rock-type landslide swell characteristics and impact for navigable conditions of the river-channel type reservoir in mountainous area［D］.Chongqing:Chongqing Jiaotong University，2013.

［16］吴宋仁，严以新.海岸动力学［M］.北京:人民交通出版社，2008.WU Songren，YAN Yixin.Coastline Hydrodynamics［M］.Beijing:China Communications Press，2008.

［17］中华人民共和国交通运输部.JTS 145—2—2013，海港水文规范［S］.北京:人民交通出版社，2013.The Ministry of Transport of the People's Republic of China.JTS 145—2—3， Code of Hydrology for Sea Harbour［S］. Beijing: China Communications Press，2013.