基于ANSYS的中压真空灭弧室内部磁场的仿真分析
2014-03-05张洪达史宗谦
孙 巍,刘 洋,张洪达,孙 晨,史宗谦
(1.黑龙江省电力科学研究院,哈尔滨 150030;2.西安交通大学,西安 710049)
在真空灭弧室用纵向磁场来控制真空电弧的形态,能够提高灭弧室的开断性能。纵向磁场对抑制真空灭弧室内部大电流电弧的收缩、降低电弧电压、防止触头表面的烧蚀以及提高弧后介质恢复强度等具有良好的效果[1]。然而,由于某些中压真空灭弧室中电弧随着电流不断增大,仍然出现收缩现象,造成了触头表面局部严重烧蚀,严重影响了电流的开断和触头的电寿命。因此,为了研究灭弧室内部的磁场分布,提高中压真空灭弧室的开断性能,本文应用Pro/Engineer软件建立了真空灭弧室内部磁场计算的仿真模型,设置了材料属性和边界条件,并采用ANSYS仿真软件对真空灭弧室内部弧柱中心平面的纵向磁场分布进行了计算,指出了影响真空灭弧室内部磁场分布的因素。而且,在可拆卸真空灭弧室中进行了电弧特性实验,获取了不同开断电流下的电弧特性,为今后中压真空灭弧室的设计提供了参考依据。
1 磁场仿真模型的建立
本文运用有限元分析法计算中压真空灭弧室内部的磁场分布,其原理:将所处理的对象划分为有限个单元(包含若干个节点),根据磁场偏微分方程求解一定边界条件与初始条件下每个节点处的矢量磁势,从而求解出磁场的其他物理量[2-3]。矢量磁势为

式中:B为磁感应强度;A为矢量磁势。
矢量磁势式(1)满足了高斯磁通定律和法拉第电磁感应定律,所以应用高斯电通定律和安培环路定律,就得到了磁场偏微分方程和拉普拉斯算子:

式中:B为磁感应强度;A为电流密度。
为了保证计算结果的准确性,本文应用Pro/Engineer软件,按照1∶1的比例建立真空灭弧室内部温度场计算的仿真模型。中压真空灭弧室内部磁场的计算模型如图1所示。

在图1中,触头之间的开距按照额定值10 mm进行设定,触头片的直径为79 mm,触头片的厚度5 mm,触头片上的径向直槽的宽度为2 mm,长度为22 mm;触头座的高度为22 mm,杯壁厚度为9 mm,触头座的杯指与水平面的夹角为25°。
2 材料属性和边界条件的设置
建立模型后,对仿真模型的各个部分设置相应的材料属性。其中,导电杆、触头座、母排和套接的材料均为纯铜;触头支撑的材料为不锈钢;触头片的材料为CuCr50;电弧的等效材料的电导率按照经验公式进行计算,本文将其设置为 2800 S/m[4],模型所用的材料属性表如表1所示。

表1 模型材料属性Tab.1 Properties of model material
由于没有在触头座中加入铁芯,因此计算模型中所有材料的相对磁导率为1。边界条件的设置:输入电流为交流电流,频率为50 Hz,有效值为3150 A,分别选取2个导电杆的端面作为电流的输入和输出面。计算场域为模型的5倍,边界磁势为0。对于瞬态磁场:通入电流的时间为1/2工频周期,即 0.01 s。
3 磁场仿真计算结果
磁场仿真计算所关注的区域是电弧模型,所以选择弧柱中心平面,即与触头片平面平行、与两触头片表面距离相等的平面。本文所给出的仿真计算结果均为弧柱中心平面纵向磁场的分布情况。其中,Bz表示纵向磁场,即沿z轴方向的轴向磁场。取坐标轴x方向为沿着阳极触头片开槽的方向,而y方向为与x方向正交的方向。
3.1 稳态磁场仿真计算结果
杯状纵磁触头能够在触头间隙产生分布比较均匀的纵向磁场。文献[6-7]对纵向磁场的空间分布和滞后时间作了细致的分析研究。在此基础上,本文将磁场仿真计算模型导入ANSYS有限元分析软件,然后按照材料属性和边界条件进行计算,得到了真空灭弧室内部弧柱中心平面的纵向磁场分布,如图2所示。

图2 触头中心平面的纵向磁场分布Fig.2 Longitudinal magnetic field contact head center plane
从图2中可以看出,杯状纵磁触头中心平面的纵向磁场最大有效值为12.35 mT,杯状纵磁触头在电弧中心平面产生“圆台形”(即“钟形”)的纵向磁场分布,圆台顶部对应于触头的6个槽有6个略微突起的峰。触头中心平面的中心处纵向磁场强度较大,最大有效值达到12.35 mT,但是此区域的纵向磁场分布比较均匀,触头边缘处的纵向磁场强度较小,可以忽略不计。
涡流效应会引起滞后,当滞后时间t大于一定值后,电弧会集中烧蚀阳极表面,致使阳极温度升高,从而对真空断路器的开断性能造成影响。因此,对滞后时间t的研究尤为重要。为了得到电弧中心平面纵向磁场的滞后时间,首先应按电弧中心平面纵向磁场的磁感应强度随时间变化的表达式进行计算,然后由其实部和虚部确认纵向磁场滞后于电流的相位角,进而计算出纵向磁场的滞后时间t。电弧中心平面沿x轴径向的纵向磁场实部和虚部的分布曲线如图3所示。电弧中心平面沿x轴径向的纵向磁场滞后时间分布曲线如图4所示。

图3 电弧中心平面沿x轴径向的纵向磁场实部和虚部的分布Fig.3 Distribution of arc center plane along x axis radial axial magnetic field of the real and imaginary part
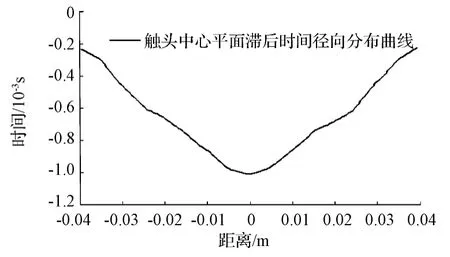
图4 电弧中心平面沿x轴径向的纵向磁场滞后时间分布Fig.4 Longitudinal magnetic field lag time distribution of arc center plane along the x axis radial
从图3中可以得出:电弧中心平面最大磁感应强度的有效值为12.35 mT,相位滞后0.32 rad,电弧中心平面上的纵向磁场的磁感应强度随时间变化的表达式为

式中:B为磁感应强度,mT。
从图4中可以看出,在电弧中心平面的中心处纵向磁场的滞后时间最长,最长滞后时间为1.01ms,在电弧边缘处纵向磁场的滞后时间最短。
3.2 瞬态磁场仿真计算结果
通过对中压真空灭弧室内部稳态磁场的计算,得到了在长期工作时间内灭弧室内部纵向磁场随时间变化的规律。但是,这并不能准确反映出在特定的较短时间内纵向磁场的变化规律,还需要进行瞬态磁场的仿真计算。所以,本文具体分析在1/2工频电流周期(0.01 s)的特定时间内,中压真空灭弧室内部纵向磁场的分布情况。
对磁场仿真模型施加1/2周期有效值为3150 A的工频交流电流,分别得到在输入电流峰值时刻和过零时刻中压真空灭弧室内部电弧中心平面的纵向磁场分布。输入电流峰值时刻,真空灭弧室内部电弧中心平面的纵向磁场分布如图5所示。电流峰值和过零时刻,真空灭弧室内部电弧中心平面沿x轴径向纵向磁场的分布曲线如图6所示。

图5 电流峰值时刻电弧中心平面的纵向磁场分布图Fig.5 Longitudinal magnetic field distribution of arc center plane at peak current

图6 电流峰值和过零时刻电弧中心平面沿x轴径向纵向磁场的分布Fig.6 Longitudinal magnetic field distribution of arc center plane along the x axis radial at current peak and zero crossing time
从图5和图6中可以看出:1)在输入电流的峰值时刻,电弧中心平面的纵向磁场呈“钟”形分布,电弧中心平面的中心区域纵向磁场强度较大,最大有效值达到17.9 mT,但是此区域的纵向磁场分布比较均匀,电极边缘处的磁感应强度较小,可以忽略不计。2)在输入电流的过零时刻,电弧中心平面仍然存在最大值为5.9 mT的剩余磁场,这部分纵向磁场是由涡流作用产生的。其中,剩余磁场越小,越有利于电流过零时绝缘介质强度的恢复,从而越有利于电流的成功开断。
3.3 真空灭弧室内部纵向磁场分布影响因素的分析
3.3.1 触头支撑对磁场分布的影响
在以往的仿真计算中,中压真空灭弧室的触头内部是有触头支撑的,为了研究触头支撑对电弧中心平面纵向磁场分布的影响,在其他计算条件不变的情况下,分别对触头座中有无触头支撑进行对比计算,在电流峰值时刻,两种情况下的电弧中心平面沿x轴径向的纵向磁场分布曲线如图7所示。

图7 沿x轴径向的纵向磁场分布曲线Fig.7 Axial magnetic field distribution along the x axis radial
从图7可以看出,当去掉触头支撑后,电弧中心平面的磁感应强度略微增大。这是因为触头支撑的材料为不锈钢,不锈钢的电导率虽小于铜,但仍会起到一定的分流作用。
3.3.2动、静触头的位置对纵向磁场分布的影响
为了研究动、静触头的放置位置对电弧中心平面纵向磁场分布的影响,在其他计算条件不变的情况下,分别对动、静触头处于错开30°与错开0°的两种位置进行对比计算。在电流峰值时刻,动、静触头处于错开30°时,电弧中心平面的纵向磁场分布如图8所示。在电流峰值时刻,动、静触头处于错开0°时,电弧中心平面的纵向磁场分布如图9所示。
从图8和图9中可以看出,当动、静触头错开0°时,电弧中心平面有6个比较明显的峰;当动、静触头错开30°时,电弧中心平面的纵向磁场分布更加均匀。这是因为在触头片的开槽区域的涡流比较小,导致在触头片的开槽区域的纵向磁场感应强度的较大所致。

图8 动、静触头处于错开30°时电弧中心平面的纵向磁场分布图Fig.8 Longitudinal magnetic field distribution of arc center plane at dynamic,static contact in a staggered 30°
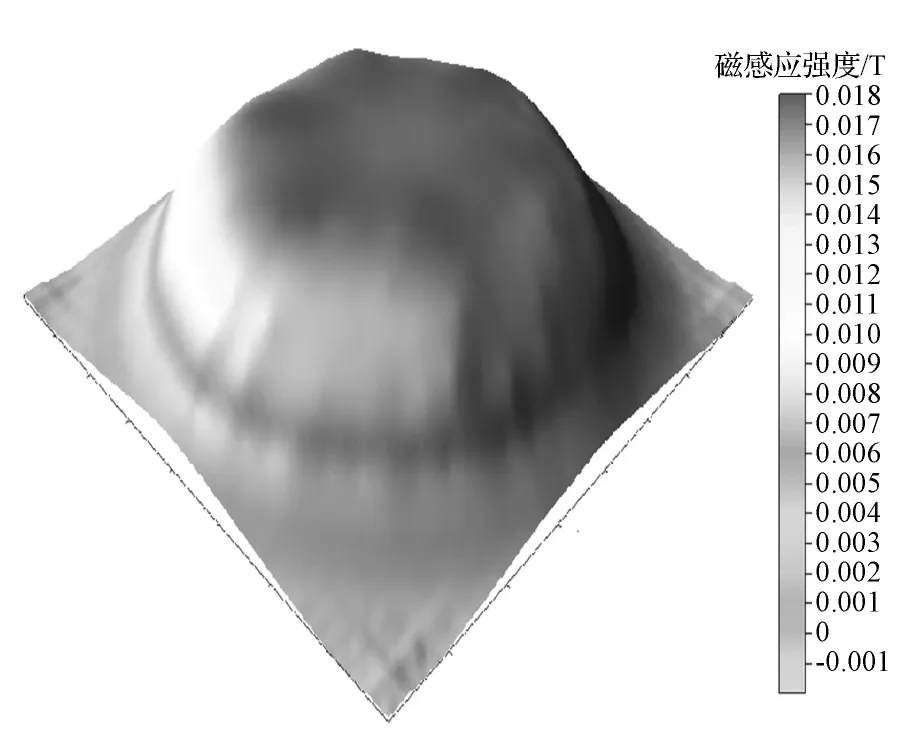
图9 动、静触头处于错开0°时电弧中心平面的纵向磁场分布图Fig.9 Longitudinal magnetic field distribution of arc center plane at dynamic,static contact in a staggered 0°
3.3.3 触头的杯指与水平面的夹角对磁场分布的影响
在以往的仿真中,真空灭弧室内部的触头的杯指与水平面的夹角为25°,为了研究触头的杯指与水平面夹角对电弧中心平面纵向磁场分布的影响,在其他计算条件不变的情况下,分别改变触头的杯指与水平面的夹角,进行对比计算。在电流峰值时刻,杯指与水平面夹角为25°和27°时电流峰值时刻,两种情况下的电弧中心平面沿x轴径向的纵向磁场分布曲线,如图10所示。
从图10中可以看出,触头的杯指与水平面的夹角越小,电弧中心平面的纵向磁感应强度越大。这是因为触头的杯指与水平面的夹角小时,杯中电流的水平分量要大于杯指与水平面的夹角大时的情形,从而导致电弧中心平面的纵向磁场强度上升。

图10 纵向磁场分布曲线Fig.10 Longitudinal magnetic field distribution curve
4 真空电弧特性实验
4.1 实验装置及主要实验设备
电弧特性实验的主线路如图11所示。实验在可拆卸式真空灭弧室内部进行,灭弧室内部的气压为4×10-4~7×10-4Pa。实验电流由单频 LC 振荡回路提供,频率为50 Hz。实验电极的位置:上面的触头为阳极,下面的触头为阴极。

图11 电弧特性实验的主线路图Fig.11 Main line circuit of arc characteristics experiment
实验采用火花触发的方式产生电弧,用高速摄影仪拍摄电弧的形态。电弧的电压和电流分别通过高压探头和分流器进行测量,实验电极开距为10 mm。实验电流的有效值分别为5 kA、10 kA、15 kA、20 kA和25 kA。为了保证实验电极表面的清洁,在加载实验电流前,先对电极进行小电流电弧老炼处理。
4.2 不同开断电流下的电弧特性对比
为了对比不同开断电流等级下电弧特性,不改变其他因素,在开断电流有效值分别为5 kA、10 kA、15 kA、20 kA和25 kA的条件下对灭弧室样品中的触头进行一系列实验。获得了如图12所示的t=5 ms(电流峰值时刻)和t=10 ms(电流过零时刻)时不同电流等级下触头间的电弧形态图像。
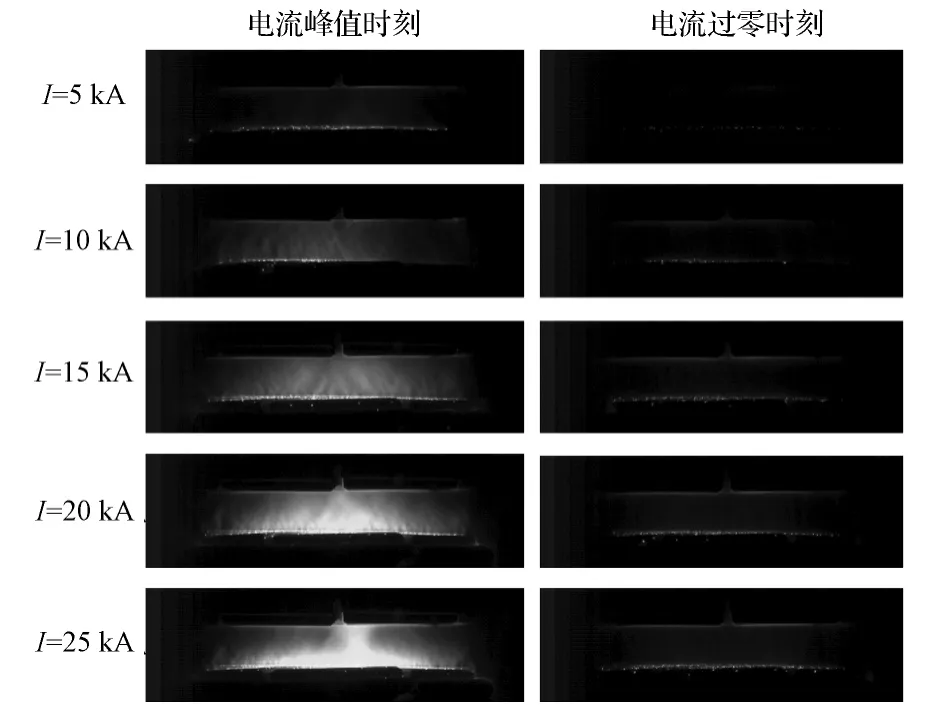
图12 不同电流等级下触头间的电弧形态Fig.12 Arc form of contact lead under different current grades
从图12中可以看出,随着电弧电流的逐步增大,弧柱区由暗变亮,触头之间阴极斑点的密度也相应的增大,并且沿径向方向,从弧柱中心区域到弧柱外缘,阴极斑点密度的梯度随电流的增大而增大。当电弧电流I=5 kA时,在电流峰值时刻,弧柱区很暗,只有阴极表面有比较明亮的阴极斑点分布;在电流过零时刻,阴极表面基本没有阴极斑点的分布。当电弧电流I=10 kA时,在电流峰值时刻,弧柱区比较暗,阴极表面分布着明亮的阴极斑点;在电流过零时刻,阴极表面分布着比较暗淡的阴极斑点。当电弧电流I=15 kA时,在电流峰值时刻,弧柱区变得明亮,而且最明亮的区域靠近阴极表面,电弧在接近阳极位置有明显的收缩;在电流过零时刻,阴极表面分布着比较明亮的阴极斑点。当电弧电流增大到I=20 kA时,这样的分布更加明显,阴极斑点密度的最大值出现在阴极中心区域,而且越靠近阳极,阴极斑点的密度越小,电弧收缩更加明显。当电弧电流I=25 kA时,在电流峰值时刻,弧柱区最明亮,而且最明亮的区域靠近阴极表面,电弧在接近阳极位置有非常明显的收缩;在电流过零时刻,阴极表面分布着明亮的阴极斑点。
5 结论
1)在稳态情况下,在触头中心平面产生“钟形”分布的纵向磁场,纵向磁场的最长滞后时间为1.01 ms。
2)在1/2工频电流周期内,在电流峰值时刻,触头中心平面的纵向磁场呈“钟形”分布;在电流过零时刻,存在最大值5.9 mT的剩余纵向磁场。
3)在触头中加入触头支撑时,由于其分流作用,电弧中心平面的磁感应强度略微减小;动、静触头错开30°时,电弧中心平面的纵向磁场分布更加均匀;在一定范围内减小触头的杯指与水平面的夹角,电弧中心平面的纵向磁感应强度增大。
4)随着电弧电流的逐步增大,弧柱区由暗变亮,极间阴极斑点的密度也相应的增大。
[1]王季梅.真空开关[M].北京:机械出版社,1983.WANG Jimei.Vacuum switch[M].Beijing:China Machine Press,1983.
[2]马信山,张济事,王平.电磁场基础[M].北京:清华大学出版社,1995.MA Xinshan,ZHANG Jishi,WANG Ping.Fundamentals of electromagnetic fields[M].Beijing:Tsinghua University Press,1995.
[3]吕英华.计算电磁学的数值方法[M].北京:清华大学出版社,2006.LYU Yinghua.Numerical method for electromagnetism calculation[M].Beijing:Tsinghua University Press,2006.
[4] FENSKI B,LINDMAYER M.Vacuum interrupters with axial field contacts 3-d finite element simulation and switching experiments[J].IEEE Trans. Dielectrics Insulation, 1997,4(4):407-412.
[5]梁淑华,范志康,胡锐.CuCr50触头材料优化热处理工艺研究[J].金属热处理学报,2000(3):66-70.LIANG Shuhua,FAN Zhikang,HU Rui.Investigation on the optimum heat treatment process of CuCr50 contact materials[J].Transactions of Metal Heat Treatment,2000(3):66-70.
[6] K NITTA,K WATANABE,K KAGENAGA,et al.Three-dimensional Magnetic Field Analysis of Electrodes for VCBs[J].IEEE Trans.Power Delivery,1997,12(4):1520-1525.
[7] STOVING P N,BESTEL E F.Finite Element Analysis of AMF Vacuum Contacts[A].IEEE EMBED Equation.3 Int.Symposium on Discharges and Electrical Insulation in Vacuum[C],Eindhoven,1998:522-529.
