基于稳定图和矩阵束算法的SSR模态识别

张宇辉，张亚鹏，李 哲，亓 亮

(1．东北电力大学 电气工程学院，吉林 吉林 132012;2．东北电力设计院，长春 130000)

在电力系统发生次同步谐振(SSR)时，由于同步发电机定子电流中的次同步频率分量所产生的负阻尼与电机中的各种阻尼大小关系存在不确定性，导致SSR可能存在三种振荡模式，即增幅性振荡、等幅振荡和衰减振荡。传统的检测方法如FFT和小波理论等方法得到的信息量有限，无法准确判断SSR的发展趋势［1］;现有的模态识别方法如prony算法和TLS－ESPRITS等方法又存在抗噪性弱、检测精度不足的问题［2－3］;刚刚启用的矩阵束算法尽管具有人为确定的参数少、检测精度较高、计算量少等优点，但其模型定阶却尤为关键［4］。为此，本文采用稳定图的方法来为模型定阶。在含噪条件下，利用稳定图法可以准确地确定出系统的阶数，有效杜绝虚假模态的干扰［5］，然后运用矩阵束方法检测系统精确频率，针对次同步振荡的特征频率进行模态识别，分析出次同步振荡的频率、振幅和衰减因子。仿真结果验证，结合稳定图的矩阵束方法可以有效辨识出SSR特征信号。

1 矩阵束算法

矩阵束方法可以用于从系统的扰动响应中直接提取与振荡模态有关的信息，如模态的频率、幅值、衰减因子等。

将含噪的平稳信号描述为

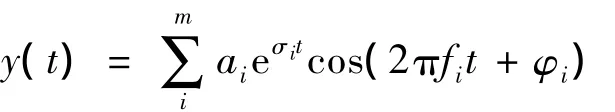
式中:i为模态序号;m为最大模态数;ai、φi为第i个振荡模态的幅值和初相位;σi为模态阻尼;fi为模态振荡频率值。

利用 WAMS实测信号y(k)(k=1，2，…，N)作为采样信号，构造如下Hankel矩阵:

式中L为矩阵束的参数，恰当选取L可以有效地抑制噪声干扰，通常L=N/4～N/3。

将Hankel矩阵Y进行奇异值分解，得

取对角阵S中前M个较大的奇异值σi所在的列构成矩阵S1，σi对应的右奇异向量vi构成V'=［v1，v2，…，vM］。将矩阵 V 的第一行删去构成 V1，最后一行删去构成V2。定义

令zi=e(－αi+jwi)k，可以证明:zi是矩阵束 Y2－ λY1的广义特征值，即求解

求出G的n个特征值λi后，设Ts为采样周期，利用λi可以得到频率和衰减因子σi:

2 稳定图法

时间序列方法在系统参数识别中，模型定阶是最关键一步。稳定图法是一种模型定阶的有效方法，其主要思想是:假定系统具有不同的阶次，绘出一个以频率为横坐标、阶次为纵坐标含有各阶次的模态参数二维图。随着阶数的增加，真实模态和噪声等因素所产生的虚假模态会同时出现在稳定图上，真实模态对应的极点会出现在每个阶次固定的频率上，在稳定图上表现为一条竖线，形成一条稳定轴;而虚假模态对应的极点则呈分散形态，没有稳定轴，利用这一特征可以将真实模态与虚假模态进行区分，实现系统定阶。

2．1 稳定图定阶原理

将原始信号y(k)(k=1，2，…，N)构造为Hankel矩阵:

式中:下标0/2i－1表示Hankel矩阵第1列的第1个和最后1个元素;下标p和f分别表示过去和将来;下标i表示两个输出的时间间隔;j表示计算系统输出协方差所取的输出数据的组数，j尽量大。利用Y0/2i－1矩阵构造协方差Toeplize矩阵:

对Toeplize矩阵进行奇异值分解，以达到消除噪声的目的:

构造系统的为可观测矩阵Oi与反转可控随机矩阵 Γi。因 T1，i=OiΓi，可得到系统矩阵 A 为

将A阵进行奇异值分解可得到系统的特征值λi及系统的各种特征参数进而绘制出稳定图。

2．2 利用稳定图定阶的具体步骤

1)设系统阶数为n，并假定系统的最大阶次和最小阶次分别为nmax和nmin，故nmin≤n≤nmax，且n为偶数，得到(nmax－nmin)/2+1个假定阶次。

2)对每一个n值都进行一次模态识别，将得到的(nmax－nmin)/2+1组结果绘入以频率为横坐标、阶次为纵坐标的稳定图中。

3)在稳定图中，如果有一条轴上的点满足式(1)，则该轴确定为稳定轴，稳定轴的个数就是系统阶数:

式中:i为模型阶次;fi为在阶次i下的模态频率;δf为容差率。

借助稳定图可以获得正确的模型阶数和模态参数，杜绝了虚假模态对系统定阶的影响。

3 算法实现步骤

基于稳定图和矩阵束算法的SSR检测步骤如下:

1)提取发电机转子转矩信号为检测信号。

2)根据稳定图法判断信号中的频率成分给模型定阶。

3)利用矩阵束算法计算出检测信号中各分量频率的精确值，检测其是否含有SSR特征频率。

4)提取转矩信号中出现SSR的特征频率，用矩阵束方法来辨识出该频率分量的幅值、衰减因子等参数借此判断其发展趋势。

4 仿真试验

4．1 算例分析

以s(t)=1．5e－0．2tsin(2π×150t+π/4)+0.5e－0．5tsin(2π×100t+π/+e－1．3tsin(2π×50t+π/5)+n(t)为检测信号。其中n(t)为高斯白噪声，检测信号中信噪比为10 dB，波形如图1所示。信噪比定义为

图1 检测信号波形Fig．1 Waveform of the detection Signal

利用稳定图为模型定阶，设容差率δf=1.5%，检测信号稳定图如图2所示。

由图2可以看到模型中含有3个频率分量，因为含有噪声，将模型阶数定为8。

图2 检测信号稳定图Fig．2 Stabilization diagram of detection signal

相对误差定义为

分别采用矩阵束方法与TLS－ESPRITS方法进行检测，结果如表1所示。

从表1可以看出，在同等噪声强度的环境下，矩阵束方法对频率、衰减因子的检测精度优于TLS－ESPRITS方法。

4．2 仿真实例

采用IEEE第二基准SSR标准模型进行仿真［6］，如图3 所示 。

图3 系统接线图Fig．3 System wiring diagram

在图3中，同步发电机轴系模型由多个质量模块构成［7－8］，如图 4 所示。

图4 发电机轴系模型Fig．4 Generator shaft model

各质量模块间的一阶自然扭振频率分别为24.6 和 32．8 Hz。

在不同串补度的条件下，通过定子进入发电机的电气谐振频率不同，引起发电机转子转速信号的变化趋势也不同。采用大扰动条件下获得的发电机机械量:2 s时系统在图3中L2线上发生三相短路故障，持续0．017 s，采样频率fs=1000 Hz。分别提取系统串补度为30%和60%时的转子低压缸和高压缸之间的转矩信号为特征信号，再向信号中加入噪声，令其信噪比SNR=10 dB，得到信号如图5所示。

由图5作出判断，当系统串补度分别为30%和60%时，转子转矩信号分别呈现出衰减振荡和增幅性振荡的趋势。据此，分别绘制串补度为30%和60%时的转子低压缸和高压缸之间转矩信号的稳定图，如图6所示。

由图6可以看到，2个转矩信号中都存在着2个频率分量。由于噪声的存在，系统的阶数为6。使用矩阵束方法进行SSR模态辨识，辨识结果如表2所示。

表1 矩阵束方法辨识结果Tab．1 Identification results of matrix pencil method

图5 发电机转子转矩信号Fig．5 Generator rotor torque signal

图6 发电机转子转矩信号的稳定图Fig．6 Stability diagram of generator rotor torgue signal

表2 矩阵束结合稳定图方法SSR检测结果Tab．2 SSR test results of matrix pencil algorithm combined with Stabilization diagram

由表2可以看出，转矩中出现了频率为32．42 Hz和24．72 Hz的次同步振荡特征信号。在系统的串补度为30%时，24．81 Hz振荡模式占主要成分，衰减因子为正;32．42 Hz振荡模式初始幅值较小，衰减因子为负值，转子发生了严重的SSR。该结论与发电机的转矩信号图相吻合，说明结合稳定图的矩阵束方法可以准确辨识SSR模态参数。

4．3 检测方法的性能试验

4．3．1 抗噪性

在不同信噪比条件下采用结合稳定图的矩阵束方法进行检测，采样点数为4000点，结果如表3所示。

表3 不同信噪比下矩阵束结合稳定图方法检测结果Tab．3 Detection results of matrix pencil algorithm Combined with Stabilization diagram under different SNR

从表3可以看出，结合稳定图的矩阵束方法具有很强的抗噪性，在信噪比达到－10 dB时依然具有很高的检测精度。有必要指出，在信噪比低于－10 dB时，结合稳定图的矩阵束方法检测精度明显下降。

4．3．2 准确性

利用不同取样时间长度的信号进行检测，令SNR=10 dB，检测结果如表4所示。

表4 矩阵束结合稳定图方法在不同取样时间长度内的检测结果Tab．4 Detection results of matrix pencil algorithm combined with Stabilization diagram in different sampling length of time

由表4可以看出，结合稳定图的矩阵束检测方法在较短的数据长度下也能够达到较高的检测精度，实时性好。

5 结语

本文采用矩阵束结合稳定图对电力系统次同步振荡进行模态识别，通过仿真验证，在不同的串补条件下，该方法可以迅速、准确地辨识出SSR参数及其发展趋势，具有抗噪性强、检测精度高的优点。同时该方法也为SSR的在线监测提供了新的思路。

［1］张昊，石铁洪，刘沛．基于双正交小波和复小波的SSR检测方法［J］．中国电机工程学报，2001，21(3):12-15．ZHANG Hao，SHI Tiehong，LIU Pei．The detection of torsional oscillation based on the bi－orthogonal wavelet and complex wavelet［J］．Proceedings of the CSEE，2001，21(3):12 － 15．

［2］ 董青迅，李兴源，穆子龙，等．基于Prony算法的SSR检测方法［J］．电力系统及其自动化报，2012，24(2):1-4．DONG Qingxun，LI Xingyuan，MU Zilong，et al．New Method for detection of subsynchronous resonance baced on prony algorithm［J］．Proceedings of the CSU －EPSA，2012，24(2):1 －4．

［3］ 李天云，于海峰，任慧超，等．TLS－ESPRIT算法在SSR在线监测中的应用［J］．电力系统保护与控制，2011，39(12):37-41．LI Tianyun，YU Haifeng，REN Huichao，et al．TLS-ESPRIT algorithm’application in sub-synchronous resonance on line Monitoring［J］．Power System Protection and Control，2011，39(12):37-41．

［4］ OVERSCHEE V P，DEMOOR B．Subspace algorithms for the stochastic identification problem［J］．Automatic，1993，29(3)，649-660．

［5］李天云，袁明哲，许广婷，等．基于随机子空间结合稳定图的间谐波高精度检测方法［J］．电力系统自动化，2010，34(20):50-54．LI Tianyun，YUAN Mingzhe，XU Guangting，et al．An Inter-harmonics High-accuracy Detection Method Based on Stochastic Subspace and Stabilization Diagram［J］．Automation of Electic Power Systems，2010 ，34(20):50-54．

［6］ IEEE Subsynchronous Resonance Working Group of the Dynamic System Performance Subcommittee Power System Engineering Committee．Second benchmark model for computer simulation of subsynchronous resonance［J］．IEEE Transactions on Power Apparatus and Systems，1985，104(5):1057-1066．

［7］李伟，肖湘宁，赵洋．无功发生源抑制次同步振荡的机理分析［J］．电工技术学报，2011，26(4):168-174．LI Wei，XIAO Xiangning，ZHAO Yang．Mechanism analysis of static var source depressing subsynchronous oscillations［J］．Transactions ofChinaElectrotechnicalSociety， 2011，26(4):168-174．

［8］和鹏，白菲菲，张鹏，等．电力系统次同步振荡轴系模型研究［J］．电力系统保护与控制，2012，40(4):107-112．HE Peng，BAI Feifei，ZHANG Peng，et al．Shaft models of subsynchronous oscillation in power system［J］．Power System Protection and Control，2012，40(4):107-112．