STATCOM与发电机励磁的多指标协调控制

谢醉冰，文飞

(1.国家电网公司西北分部，陕西西安 710048;

2.国网湖南省电力公司衡阳供电分公司，湖南衡阳 421001）

STATCOM与发电机励磁的多指标协调控制

谢醉冰1，文飞2

(1.国家电网公司西北分部，陕西西安 710048;

2.国网湖南省电力公司衡阳供电分公司，湖南衡阳 421001）

针对单机无穷大系统，使用多指标非线性控制方法，建立6阶非线性数学模型，实现凸极式发电机励磁与STATCOM的协调控制。从STATCOM内部结构入手，采用STATCOM的脉冲控制角θ和STATCOM超前系统电压角α为控制量，克服了以往的STATCOM模型的约束条件，提高了STATCOM与发电机励磁协调控制的动、静态性能。仿真结果同线性最优控制方法比较，并验证了所建STATCOM模型和所求非线性控制率u的合理性和有效性。

STATCOM;静止同步补偿器;凸极式发电机;多指标非线性控制;协调控制

近年来，随着省际间的高压输电网络实现闭环远行，我国电力系统得到长足的发展。柔性交流输电系统 (flexible AC transmission system，FACTS)作为一种基于现代电力电子技术的新型电力系统网络技术，正逐步被电力系统广泛采用。静止同步补偿器 (static synchronous compensator，STATCOM)作为FACTS家族的重要成员，与其他FACTS元件相比较，具有控制特性好、谐波含量小、响应速度快等一系列优点，当电力系统遭遇大扰动时，能在动态过程中通过快速无功吞吐为系统提供电压支持，减少系统故障恢复时间，确保电能质量〔1-3〕。发电机内部结构复杂，具有较强的非线性，其励磁控制一直是提升电力系统稳定性和抑制低频震荡的重要手段之一。因此，如何将STATCOM与发电机励磁控制相协调，改善系统运行性能，成为一项极具理论研究价值和实际工程意义的工作〔4〕。

目前已有的文献大多是以提高发电机机端电压的控制精度和改善电力系统的动、静态性能作为研究目标〔5〕。文献〔6-8〕针对单机无穷大系统，建立了经典3阶发电机同STATCOM的协调控制模型。但文献假设发电机的输入暂态电势恒定不变，STATCOM注入点电压始终与d轴同向，在理论和实际运用中存在局限性。同时绝大多数文献都将STATCOM视为一个整体，仅以元件的注入电流和有功功率、无功功率作为参照量来研究其对维持电力系统稳定性的影响，过于笼统，不能直观地反映STATCOM元件的优越性。

文中在前述文献研究工作的基础上，基于STATCOM的结构特点，以STATCOM内部并联电容的直流电压Udc为切入点，以PWM逆变器的脉宽控制角θ和STATCOM注入电压与系统电压的超前角α为控制量;在单机无穷大系统中，利用帕克变换，在d-q坐标系中建立含有隐函数的6阶非线性系统模型。文中拟采用多指标非线性控制方法(Multi-index nonlinear control，MNC)，通过选取确当输出函数h(x)组合，进行非线性变换，将原系统分成线性子系统和非线性子系统两部分，利用线性最优控制理论求出线性子系统的控制率v，最后反代，求出原系统的非线性控制率u。该方法避免进行繁杂的完全精确线性化〔9〕，很好地解决了含隐函数非线性系统的控制问题。

1 数学模型

1.1 发电机模型的建立

考虑到工程实际，采用某电厂353 MVA三阶凸极式发电机模型，即x'd≠xq(为简化，此处不计发电机的定子绕组，忽视调速器的影响)，有

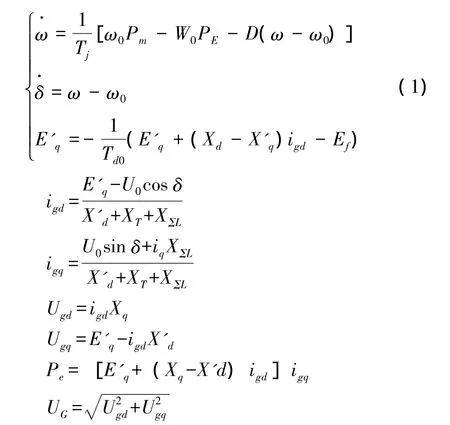
式中 Ef为发电机折算到定子侧的励磁电势;E'q为发电机的空载电势;Pm为发电机的机械功率;Pe为发电机电磁功率;Xd为发电机直轴电抗;Xq为发电机交轴电抗;X'd为发电机直轴的暂态电抗;XT为变压器的等效电抗;ω为发电机转子角速度;ω0为发电机转子同步角速度;Tj为发电机转子的惯性时间常数;T'd0为发电机定子开路时励磁绕组的时间常数;D为发电机阻尼系数;δ为无穷大处母线电压与q轴的夹角。

1.2 STATCOM模型的建立

工程实际中，STATCOM装置根据其内部结构的不同，主要有电压型整流桥和电流型整流桥2种，其区别在于前者直流侧采用电容作为储能元件而后者采用电感元件。文中拟采用电压型大容量链式STATCOM，其内部A，B，C三相逆变桥，每相由2个IGBT管并联组成。STATCOM的具体结构图如图 1 所示〔10-11〕。

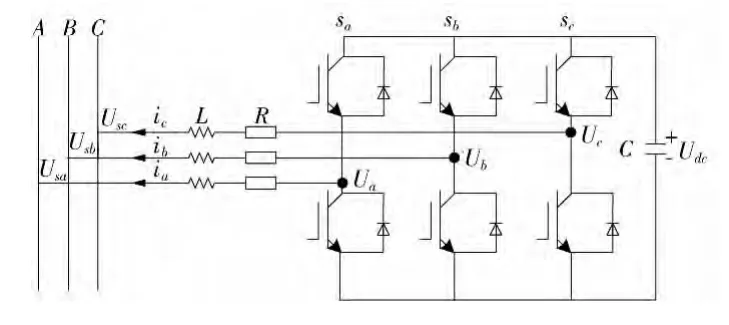
图1 STATCOM的电路结构

假设STATCOM直流电容原先储能为0，且能量通过他励方式从系统获得。根据能量守恒定律，在不考虑零序电流的情况下假设三相电流和为零，建立STATCOM的动态模型如下:

分析2011年7月至2017年9月在温州医科大学附属眼视光医院行眼球摘除、眼内容物剜除、眶内容物剜除术患者的临床资料，共676例（676眼），其中男437例，女239例，321只右眼，355只左眼；年龄7个月～90岁[（46.9±20.1）岁]。在676例患者中眼球摘除230例，占34.0%；眼内容物剜除426例，占63.0%；眶内容物剜除20例，占3.0%。

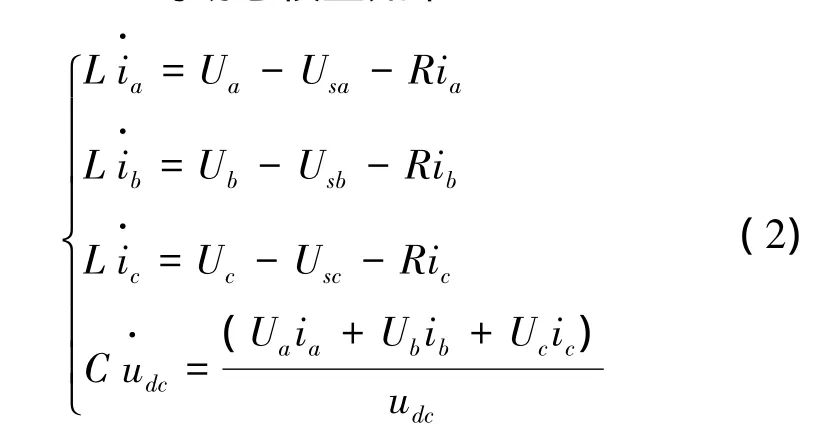
式中 L为换流器侧变压器的等效电感;R为STATCOM逆变桥内阻和IGBT的导通电阻的等效值;Ua，Ub，Uc分别为逆变桥A，B，C三相输出交流电压;Usa，Usb，Usc分别为 STATCOM 的 A，B，C三相在注入点S处的电压值;ia，ib，ic分别为STATCOM流入注入点的A，B，C三相电流;C为并联直流电容;Udc为逆变桥的直流电压。

图2为STATCOM支路的电压相角图。从图中可以等到如下数学关系。

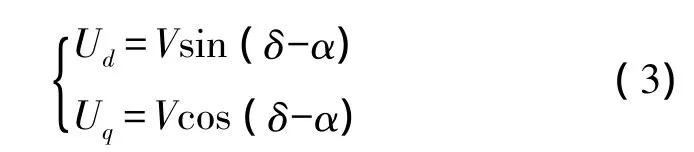
式中 δ为无穷大处母线电压与q轴的夹角;α为STATCOM交流侧电压与系统电压的相位差。

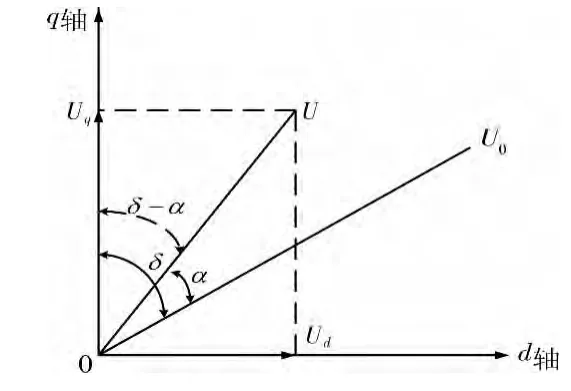
图2 STATCOM支路的电压相角

根据文献〔7〕，可以得到STATCOM交、直流侧电压的互换关系:

式中 θ为电压型逆变器采用脉宽控制方式(PWM)时的脉宽控制角;Udc为逆变桥的直流电容电压;k为交、直流电压互换参数，由STATCOM的内部结构决定。文中采用单相逆变桥:k=4/π。

根据STATCOM支路电压的相角关系 (参见图2)，将式 (2)经帕克变换转换到 d-q坐标系中〔12〕，可以得到STATCOM的三阶动态模型。

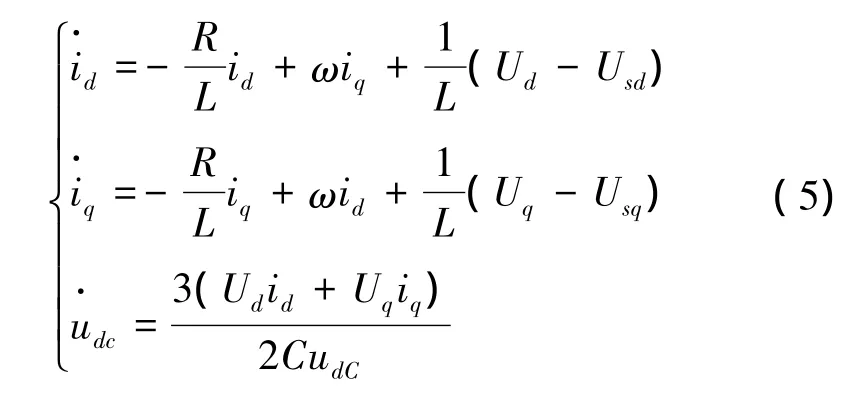
式中 U为STATCOM交流侧的电压;Ud，Uq分别为STATCOM交流侧电压在d轴和q轴的分量。

1.3 SMIB系统模型的建立

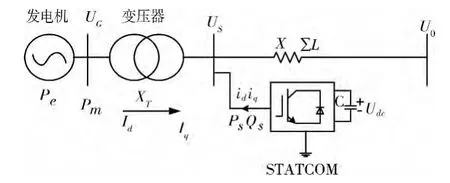
图3 装设STATCOM的SMIB等值电路图

结合式 (1)，(3)，(4)，(5)，建立SMIB系统的非线性动态方程。

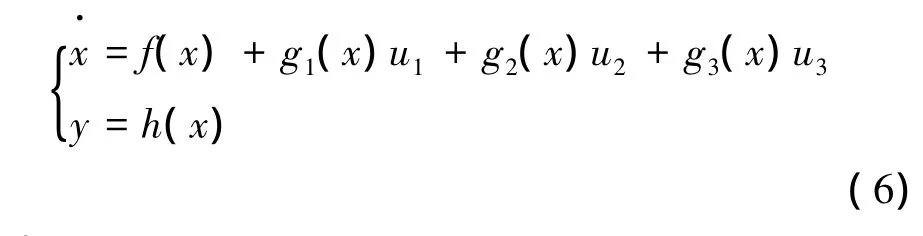
式中

式中 δ，ω，E'q，id，iq，udc为状态变量，u1，u2，u3为控制变量。

2 STATCOM非线性控制律的设计

根据二次性能指标公式:

式中 z是非线性系统变换坐标，v是线性部分的最优反馈控制规律。可知，选取符合二次性能指标的状态量构成输出函数h(x)，能有效地改进系统的动、静态性能。文中拟选取输出函数的主要依据如下:

1)选取与发电机励磁控制变量Ef相对应的输出函数h1(x)。发电机励磁控制的首要任务是保证发电机机端电压的稳定性，频率f是衡量电能质量的重要指标，而转子角速度ω与频率息息相关，故h1x中应含有角速度的偏差量Δω和发电机机端电压的偏差量 ΔUG∶h1(x)=c1Δω+c2ΔUG。

2)选取与STATCOM注入电流d轴分量id相对应的输出函数 h2(x)。该控制量主要由STATCOM装置的有功功率决定，故选取STATCOM的有功偏差ΔPs作为状态量;同时为了保证精度，选取STATCOM的有功电流偏差 Δid为状态量:h2(x)=c3ΔPs+c4Δid。

3)选取与STATCOM注入电流q轴分量iq相对应的输出函数 h3(x)。该控制量主要由STATCOM装置的无功功率决定，故选取STATCOM的无功偏差ΔQs作为状态量;考虑到注入点电压的支撑作用，选取注入点电压的偏差ΔUs作为状态量;同时为了保证精度，选取STATCOM的无功电流偏差Δiq作为状态量:h3(x)=c5ΔQs+c6Δiq+c7ΔUs。

根据非线性控制理论，将 h(x)=［h1(x)，h2(x)，h3(x)］T部分精确线性化， 得到矩阵:

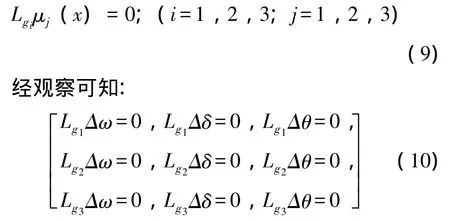
结合选取的输出函数组合及式 (10)，基于式(8)将原方程组转换成Z空间的第二标准型:

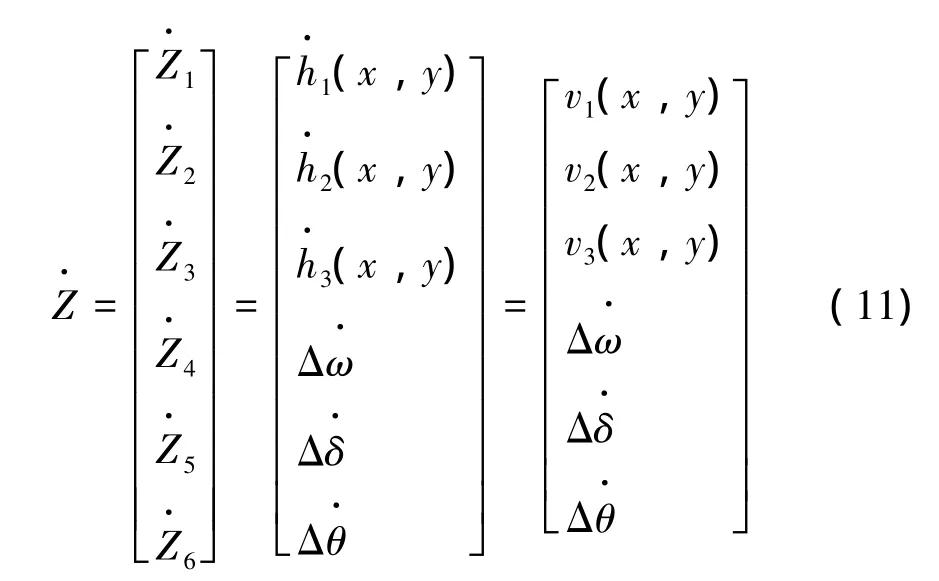
基于线性最优控制理论，可以得出原系统线性子系统的控制率v:

将v反代回式 (13)，求出原系统的非线性控制率 u= ［u1，u2，u3］T。

非线性控制率u中的c，k参数的选取方法，在文献〔13〕已有详尽论述。其主要方法是将闭环控制系统在平衡点处按泰勒级数展开，再进行相应的拉式变换，最后根据控制系统的零极点，反解出相应的c，k值。

3 数字仿真

3.1 仿真系统简介

采用MATLAB仿真，将MNC方法与LOC方法进行对比，验证MNC协调控制器的有效性。系统具体参数:XD=1.09 pu;Xq=0.727 9 pu;X'd=0.339 9 pu;XT=0.1 pu;XL=0.16 pu;ω0=314.16 rad;R=0.05 pu;L=0.1 pu;Tf=7s;T'd0=6.2 s;D=2 s。系统的初始工况:δ0=60°;Pe0=0.663 9 pu;Us0=1.0153 pu;Eq0=0.9375 pu;U0=1.0 pu。非线性控制率中c，k参数值分别为:c1=45，c2=1，c3=-4;c4=-1;c5=8;c6=4;c7=2;k1=-10;k2=-8;k3=-5。

3.2 仿真结果分析

3.2.1 调功扰动

调功扰动是指系统在正常运行1 s后，有功功率阶跃增加10%。重点考查非线性控制率u对发电机电磁功率的动态跟踪能力，同时考察这项调节对系统其它状态量暂态精度的影响。图4为该扰动下，系统各相关状态量的响应曲线。

图4(a)表明在非线性控制率u的有效控制下，系统功角会随发电机电磁功率的跃增而适度增加，与LOC控制法比较，其超调范围远小于后者;图4(c)，(d)表明非线性控制率u能精准地跟踪发电机电磁功率的变化状态，同时维持发电机机端电压的稳定;图4(b)，(e)，(f)表明该控制率能有效地调动STATCOM装置进行有、无功补偿，维持系统其他状态量的暂态精度。

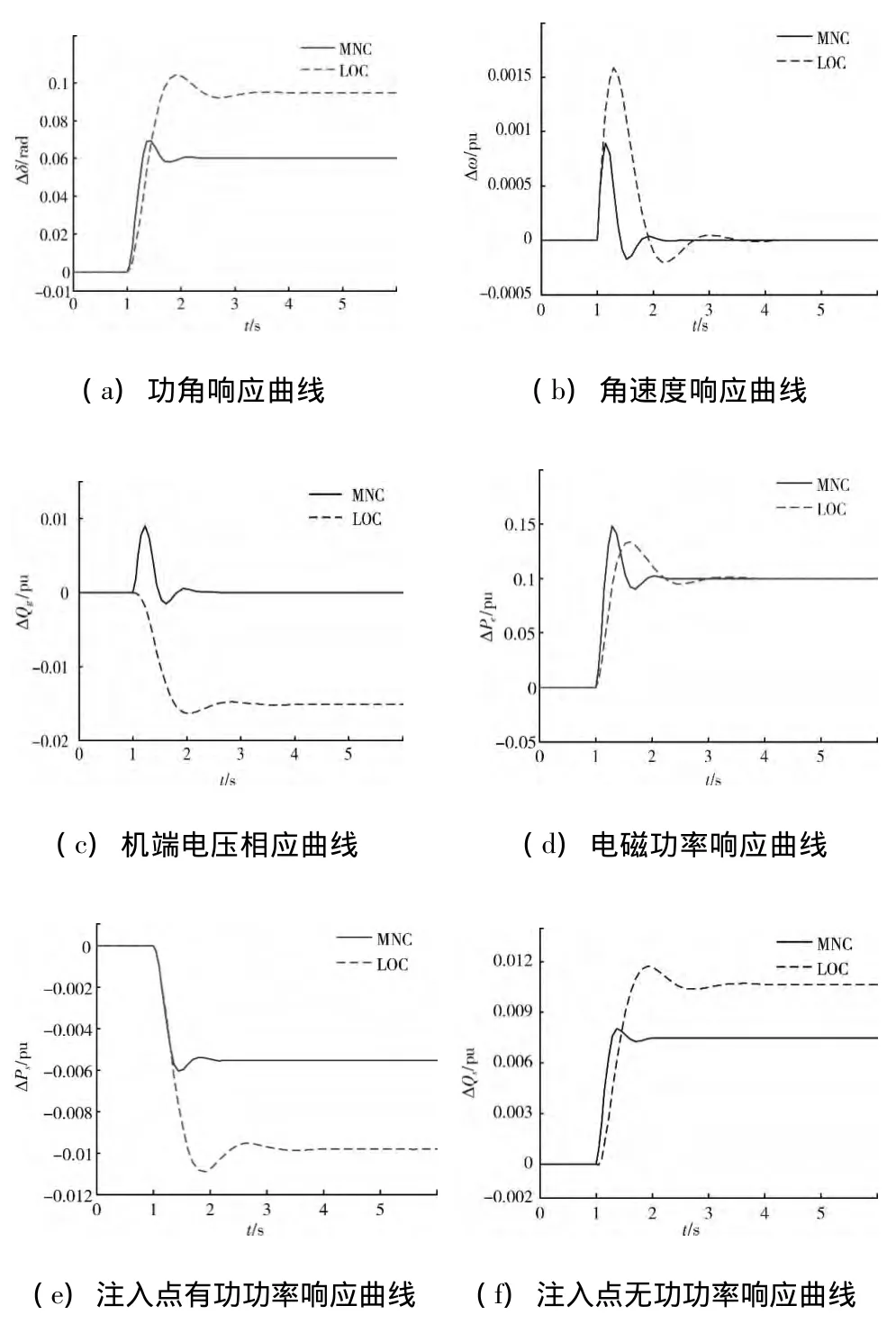
图4 发电机调功扰动时系统的动态响应曲线

3.2.2 三相短路扰动

系统正常运行1 s时，在无穷大母线处发生三相短路，0.05 s后三相重合闸成功，故障切除，系统重新回到稳定状态。图5给出了该扰动下系统各相关状态量的响应曲线。

图5(a)， (b)表明当系统发生大扰动时，非线性控制率u能迅速提高系统阻尼，较好地抑制系统震荡，维持系统功角稳定，同时能在短时间内稳定发电机的转速，防止因系统突然甩负荷而导致的发电机“失步”现象;图5(c)表明该控制率能快速、高效地维持系统电压稳定，防止因负荷消失或转速升高而引起的机端电压升高;图5(d)表明该控制率能在系统突然空载时，快速补充无功功率，确保注入点电压稳定;图5(e)，(f)表明该控制率能充分调动STATCOM为系统提供有、无功功率，减少发电机内部转子所受反向力矩的冲击，提高系统暂态稳定性和抗大扰动的能力。同LOC法比较，本法使系统在遇到大扰动时各状态量的超调量幅值和调节时间均优于后者。

图5 三相短路时系统的动态响应曲线

4 结论

文中运用多指标非线性控制法，建立了凸极式发电机励磁和STATCOM协调控制的6阶非线性数学模型，获得了一个稳定的、具有良好多指标控制效果的非线性控制率u。通过仿真表明:该控制率充分发挥了发电机励磁和STATCOM的快速有、无功补偿作用。当系统定值发生突变时，能精确跟踪系统发电机电磁功率的变化，同时保证机端电压稳定，提高系统电能质量;当系统发生诸如三相短路这样的大扰动时，能快速介入，稳定系统电压和发电机转速，防止发电机因系统突然甩负荷而出现的“失步”现象，同时触发STATCOM进行动态有、无功补偿，降低各状态量的超调量。仿真结果表明，文中设计的MNC控制率u能很好地提升系统应变突发情况的动、静态性能，优于LOC控制法，具备一定的应用价值。

〔1〕Sensarma P S，Padiyar K R，Ramanrayanan V.Analysis and performance evaluation of a distribution STATCOM for compensation voltage fluctuations〔J〕.IEEE Trans on Power Delivery，2001，16(2):259-264.

〔2〕赵渊，董力，谢开贵.FACTS元件的可靠性成本/效益分析及其优化配置模型研究〔J〕.电力系统保护与控制，2012，40(1):107-144.

〔3〕Shoorangiz S S F，Reza H，Mehdi N.Comparison of artificial intelligence strategiesforSTATCOM supplementary controller design〔J〕.World Applied Sciences Journal，2009，7(11):1 428-1 438.

〔4〕李世芳，王杰.具有代数约束的STATCOM与凸极式发电机励磁协调控制研究〔J〕.中国电机工程学报，2011，31(13):26-32.

〔5〕谢小荣，崔文进，陈远华，等.多机电力系统中STATCOM与发电机励磁的协调控制〔J〕.电力系统自动化，2002，26(1):14-17.

〔6〕 LihongG，JieW.Nonlinearcoordinated ofexcitation and STATCOM ofpowersystems〔J〕.ElectricPowerSystems Research，2007(77):788-796.

〔7〕孙元章，刘建政，杨志平，等.ASV动态建模与暂态仿真研究〔J〕.电力系统自动化，1996，20(1);5-10.

〔8〕谢小荣，崔文进，唐义良，等.STATCOM与发电机励磁的协调控制〔J〕.电力系统自动化，2001，3(10):19-22.

〔9〕李啸骢，邓裕文，游晓枫，等.单输入单输出微分代数系统的多指标非线性控制方法〔J〕.中国电机工程学报，2012，32(7):47-52.

〔10〕云平平，杨宝峰，刘永和，等.基于多级电压注入式STATCOM装置的性能研究〔J〕.电力系统保护与控制，2007，35(1)，54-62.

〔11〕邓家泽，王奔，黄崇鑫，等.基于晶闸管 STATCOM的无功补偿控制〔J〕.电网技术，2009，33(1):48-51.

〔12〕单翀皞，王奔，陈丹，等.基于滑模控制理论的STATCOM无功补偿控制策略研究〔J〕.电力系统保护与控制，2010，38(18):150-154.

〔13〕李啸骢，程时杰，韦化，等.具有多性能指标的汽轮发电机非线性综合控制〔J〕.中国电机工程学报，2003，23(4):96-101.

〔14〕卢强.电力系统非线性控制〔M〕.北京:科学出版社，2008.

Multi-index coordinated control for STATCOM and generator excitation

XIE Zui-bing1，WEN Fei2
(1.State Grid Northwest China Grid Co.，Ltd，Xi'an 710048，China;2.State Grid Hunan Electric Power Corporation Hengyang Power Supply Company，Hengyang 421001，China)

According to a single machine infinite bus(SMIB)system，the six order nonlinear mathematics model is established to realize coordinated control of salient-pole generators and STATCOM by multi-index nonlinear control scheme.This paper，starting with the internal structure of STATCOM，uses the STATCOM's pulse control angle θ and the angle α as the control amount.This new model which overcomes the previous strong constraints conditions of the STATCOM improves the nonlinear system's dynamic and steady-state performances.The simulation results which compared with the method of the Linear Optimal Control(MNC)indicate that the new STATCOM model and the nonlinear control rate u presented in this paper are reasonable and effective.

STATCOM;static synchronous compensator salient-pole generator;multi-index nonlinear control;coordinated control

TM76

B

1008-0198(2014)02-0019-05

10.3969/j.issn.1008-0198.2014.02.006

2013-06-05 改回日期:2014-03-30

book=4,ebook=130