基于改进粒子滤波的GPS接收机自主完好性监测算法*
2014-03-05王尔申庞涛曲萍萍张芝贤
王尔申,庞涛,曲萍萍,蔡 明,张芝贤
(沈阳航空航天大学电子信息工程学院,沈阳 110136)
1 引言
在卫星导航定位系统中,完好性监测是航空导航系统不可或缺的一部分,由于系统故障而引起的导航失败或者故障应该被探测和隔离以保证导航信息可靠性不受影响。接收机自主完好性监测(Receiver Autonomous Integrity Monitoring,RAIM)是一种基于一致性检验的自主完好性监测方法,它通过对冗余观测信息的检测来判断测量结果中是否含有较大卫星距离误差,当系统性能超出指定的容差级时,它能实时有效地给用户提供告警信息[1-3]。
目前,RAIM算法包括两大类:一类是利用当前伪距观测量的快照(Snapshot)算法,这类算法主要有奇偶空间法(Parity)、最小二乘残差和法(Sum of Squares of Error,SSE)、最大间隔法等,奇偶空间法和最小二乘残差和法在检测准则上是等价的;另一类是基于卡尔曼滤波的RAIM算法。卡尔曼滤波算法是通过利用历史观测量来提高效果,对先验误差特性依赖性强,而实际误差特性很难准确预测[4-5]。而且,这种算法要求测量噪声服从高斯分布,而在实际中测量噪声很难严格服从高斯分布[6],此时,该算法的性能就会降级。
为了解决上述算法对噪声分布要求的限制,将粒子滤波引入到接收机自主完好性监测中。并且为了克服基本粒子滤波重采样过程中粒子权值退化和多样性丧失的问题,将遗传算法的全局寻优的收敛性优势与神经网络局部寻优的快速性优势相结合,提出遗传算法辅助的基于神经网络权值选择的粒子滤波算法。通过该算法获取系统的状态估计并构建检验统计量,并利用对数似然比方法建立一致性检验统计量实现对故障的检测与隔离。GPS实测数据检验表明,该改进粒子滤波算法用于GPS RAIM是可行性的。
2 遗传算法辅助的神经网络算法
人工神经网络(Artificial Neural Networks,ANN)出现于20世纪40年代,通过大量的权值可变的神经元组合而成,其在并行处理数据、自组织自学习、非线性映射方面有很好的优势,被广泛应用于系统建模、信息处理、人工智能等领域。遗传算法则是一种模拟生物进化过程,通过选择、交叉和变异等操作寻找过程最优解的算法,因为其优异的全局寻优能力和能够自主优化搜索空间的能力,被广泛应用于机器学习、信号处理、自适应控制等领域[7-9]。
结合遗传算法与神经网络各自的优点,将其应用于粒子滤波算法中。利用遗传算法对神经网络初始的权值与阈值进行优化,缩短其训练时间与预测时间。利用BP神经网络对粒子滤波算法中权值过低和过高的粒子进行调整,使这些粒子向概率分布的中部移动,摒弃粒子滤波算法在采样与重采样时简单取舍的缺点,满足样本多样性的要求,最终达到提高滤波精度的目的。
3 改进粒子滤波用于GPS RAIM
采用遗传算法辅助的基于神经网络权值选择的粒子滤波算法(Genetic Algorithm Aided Neural Network Weight Adjustment Particle Filter,GANNWA -PF)用于GPS RAIM,通过建立的对数似然比(Log-Likelihood Ratio,LLR)检验统计量来实现卫星故障的检测和隔离,即通过GANNWA-PF算法对系统状态进行精确估计,计算各个时刻状态对应的LLR,将窗函数内各时刻的LLR相加得到检验统计量,得到此时刻的累加LLR[10]。通过进行一致性检查,可以实现对故障卫星的检测和隔离。
GANNWA-PF用于接收机自主完好性监测中的故障检测与隔离的系统模型建立如下。
3.1 系统状态方程和量测方程
系统状态方程为
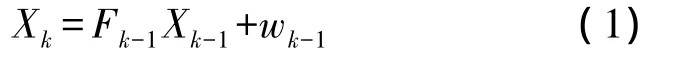
其中,X=[rx,ry,rz,Δδ],Δδ为接收机相对于卫星时间的误差;F为转移矩阵,在静止状态下为单位矩阵;w为过程噪声。
系统量测方程为

其中,ρi为接收机(rx,ry,rz)与卫星 i()之间的伪距(单位m),c为光速,Δδ为时间误差,Ei为星历影响,ε为观测噪声,Ri=为接收机与卫星i之间的真实距离(单位 m)[11]。
基于GANNWA-PF的LLR方法用于卫星故障检测和隔离的实现框图如图1所示。

图1 对数似然比检验用于RAIM原理框图Fig.1 Priciple diagram of LLR test for RAIM
例如,从GPS接收机输出的量测量数目为6,即y=[y1,y2,…,y6]T。图中的 MAIN GANNWA-PF 用于处理所有的6个量测量以对系统的状态做出较准确的估计^xM和其概率密度函数pM(y),同时其他的6个GANNWA-PF作为辅助PF主要用于分别处理6个量测量中的5个,以计算状态估计(q=A,B,…,F)和它们的概率密度函数pq(y),计算结果将用于构建检验统计量。因此,计算出主GANNWA-PF和各辅助GANNWA-PF中各时刻的粒子归一化权值,即可得到用于一致性检测的累加LLR,从而对系统是否出现故障进行检测。
3.2 LLR检验用于RAIM的原理
用于FD的判决函数如下:
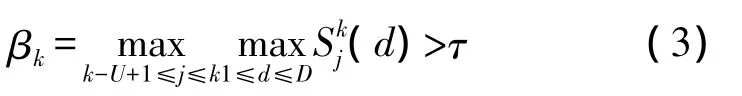
式中,U为窗函数,包含当前时刻以前的各观测时刻,τ为判决阈值。
当βk>τ,即系统检测到故障时,应当设置告警并将当前时刻表示为ta,之后利用下式确定发生故障的卫星编号:

式中,g表示故障卫星编号。确定故障卫星的卫星编号,就可以对该卫星的量测值进行隔离。
文中用到的基于GANNWA-PF算法的RAIM算法的流程如下:根据接收机所在坐标(rx,ry,rz)产生N 个主 PF的初始粒子(i),i=1,2,…,Ns}和辅助 PF 的初始粒子{(i),i=1,2,…,Ns},其中(i)=(i)。
每个时刻k重复以下步骤:
(1)状态预测
(2)计算粒子权重
(3)计算累加对数似然比;
(4)根据式(3)计算判定函数;
(5)故障判决(τ为判决阈值)
如果βk>τ,错误告警设置为ta=t时刻并跳至步骤(6)。如果 βk≤τ,则表示没有错误,跳至步骤(7);
(6)故障隔离
在k>ta下,取出Q颗卫星中累积LLR最大的那个卫星q即为出错的卫星,则g=q;
(7)状态更新
重采样得到更新粒子。
4 实测实验与结果分析
使用GPS接收机实验平台采集实验数据,同时使用另一台GPS接收机监测得到此时卫星无故障。从采集数据中提取出卫星的位置信息和伪距值。在采集到的GPS数据中,共有6颗可用于定位解算的卫星,卫星编号分别为 3、15、18、19、21、26,对应的伪距量测值为 Y=(y1,y2,y3,y4,y5,y6)。
为了验证采用GANNWA-PF算法对于GPS的RAIM的可用性和有效性,使用基于 PF算法的RAIM方法作为对比,当卫星发生故障时,通过该方法相对于采用PF的RAIM方法对比两者检测和隔离故障卫星的性能。在19号卫星的无故障状态下量测伪距数据的201~418时刻(k为201~418)中人为地加入幅度为50m的偏差数据,然后将加入误差的数据用于RAIM。实验中,神经网络隐含层神经元个数为6,训练步长为0.05,训练要求为均方误差小于10-5,粒子滤波的粒子数 N=100,用于计算判决函数的窗函数U=30。实验数据观测噪声服从高斯核拉普拉斯分布[13]。
图2和图3给出了提出的RAIM完好性监测的实验结果。式(3)中给出了用于计算故障检测的判决函数。由图2和图3可以看出,两种RAIM方法的判决函数值均在判决门限以下波动,且采用GANNWA-PF的FDI方法的判决函数的波动范围要稍小于采用基本PF的RAIM方法的判决函数。
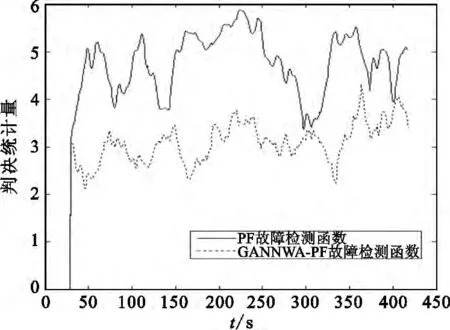
图2 正常状态下用于故障判决的检验统计量Fig.2 Decision function for fault detection under nominal condition
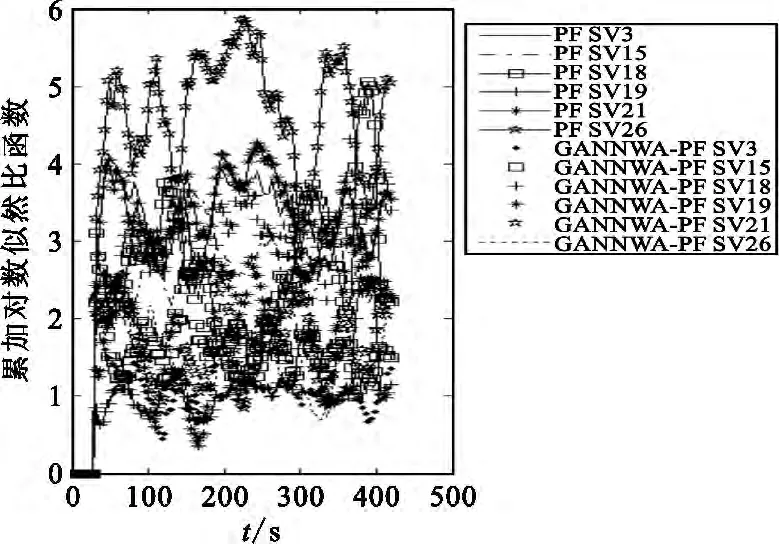
图3 正常状态下用于故障隔离的累加LLRFig.3 Cumulative LLR for fault isolation under nominal condition
图4给出了人为加入故障后的不同算法下的完好性监测实验结果。
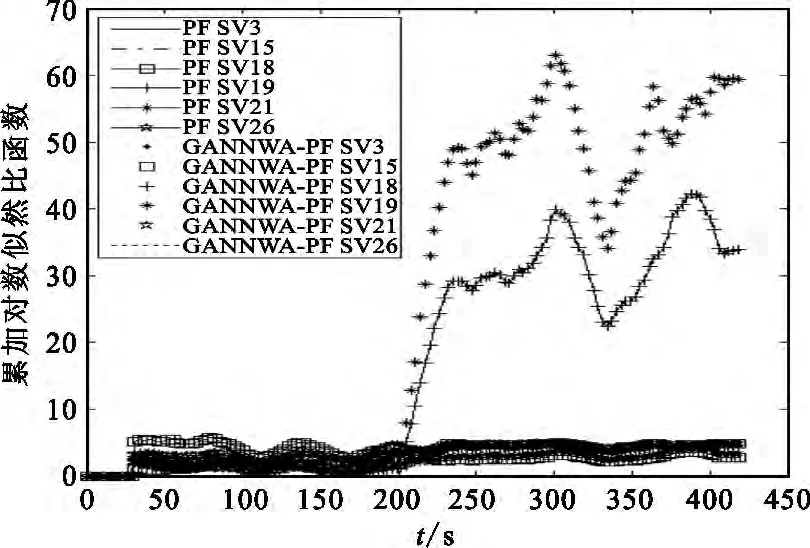
图4 故障状态下用于故障隔离的累加LLRFig.4 Cumulative LLR for fault isolation under fault condition
从图4中可以看出,在人为加入故障后,GANNWA-PF的FDI系统在k=205时刻触发告警,而采用PF的FDI发出告警的时间稍晚,且采用GANNWA-PF的FDI系统判决函数βk的跳变幅度要大于采用PF的FDI的βk跳变幅度,可使故障检测的结果更为明显,从而提高FDI的灵敏度。采用GANNWA-PF算法和基本PF算法的FDI系统都可以检测和隔离出故障卫星,采用GANNWA-PF算法的FDI系统相对于采用基本PF算法的FDI系统告警时间短,虚警概率较低,检测灵敏度较高。同时,依据文中描述的故障检测原理,可判断出故障卫星为19号卫星,在这段时间内利用卫星数据进行PVT(Position Velocity and Time)解算时应当舍弃19号卫星的观测数据,为定位结果可靠性提供保障。
5 结论
本文提出了一种遗传算法辅助神经网络的权值调整粒子滤波算法,结合遗传算法全局寻优的收敛性和神经网络局部寻优的快速性,对粒子滤波算法中的低权值和高权值的粒子进行调整,既避免了算法陷入局部极值点又加快了寻找最优估计的速度。将改进粒子滤波算法与对数似然比方法有机结合用于GPS接收机自主完好性监测。通过GPS接收机实验平台采集实测数据,利用仿真对文中研究的接收机自主完好性监测算法进行了对比验证,结果表明在非高斯量测噪声环境下,采用GANNWA-PF进行RAIM的性能优于采用基本PF算法进行RAIM的性能,验证了遗传算法辅助神经网络的权值调整粒子滤波算法用于GPS接收机自主完好性监测(RAIM)是可行的和有效的。该改进算法对于研究我国“北斗”二代导航接收机自主完好性监测具有一定的意义。
[1]徐肖豪,杨传森,刘瑞华.GNSS用户端自主完好性监测研究综述[J].航空学报,2013,34(3):451-463.XU Xiao-hao,YANG Chuan-sen,LIU Rui-hua.A Research on GNSS Client Autonomous Integrity Monitoring[J].Acta Aeronautica Et Astronautica Sinica,2013,34(3):451-463.(in Chinese)
[2]杨静,张洪钺.卫星故障诊断的最优奇偶向量法[J].航空学报,2002,23(2):183-186.YANG Jing,ZHANG Hong-yue.Satellite Fault Diagnosis Based on Optimal Parity Vector Method[J].Acta Aeronautica Et Astronautica Sinica,2002,23(2):183-186.(in Chinese)
[3]李善姬,禹爱兰.一种改进重采样的粒子滤波算法[J].电讯技术,2011,51(9):35-38.LI Shan-ji,YU Ai-lan.An Improved Resampling Particle Filter[J].Telecommunication Engineering,2011,51(9):35-38.(in Chinese)
[4]李勇,汪立新,郑海伟.一种改进的粒子滤波算法[J].电讯技术,2009,49(1):50-53.LI Yong,WANG Li-xin,ZHENG Hai- wei.An Improved Particle Filtering Algorithm[J].Telecommunication Engineering,2009,49(1):50-53.(in Chinese)
[5]Li P,Kadirkamanathan V.Particle filtering based likelihood ratio approach to fault diagnosis in nonlinear stochastic systems[J].IEEE Transactions on Systems,Man,and Cybernetics,Part C:Applications and Reviews,2001,31(3):337-343.
[6]孙国良,孙明菌,陈金平.时-集综合的接收机自主完好性监测方法研究[J].航宇学报,2006,27(6):1171-1175.SUN Guo-liang,SUN Ming-jun,CHEN Jin-ping.A Study on Time and Set Combined Mothod for Receiver Integrity Autonomous Monitoring[J].Chinese Journal of Aeronautics.2006,27(6):1171-1175.(in Chinese)
[7]李敏强,徐博艺,寇纪淞.遗传算法与神经网络的结合[J].系统工程理论与实践,1999(2):65-69.LI Min-qiang,XU Bo-yi,KOU Ji-song.The Combination of Genetic Algorithm and Neural Networks[J].Systems Engineering-Theory & Practice,1999(2):65-69.(in Chinese)
[8]杨宁,钱峰,朱瑞.基于遗传算法的改进粒子滤波算法[J].上海交通大学学报,2011,45(10):1526-1530.YANG Ning,QIAN Feng,ZHU Rui.An Improved Particle Filter Algorithm Based on Genetic Algorithm[J].Journal of Shanghai Jiaotong University,2011,45(10):1526-1530.(in Chinese)
[9]杨洋,薛晓中.遗传算法辅助下的粒子滤波及其在GPS/SINS深组合中的应用[J].解放军理工大学学报,2011,12(4):322-327.YANG Yang,XUE Xiao-zhong.Application of GA-aided Particle Filter In Tight Coupling GPS/SINS System[J].Journal of PLA University of Science and Technology,2011,12(4):322-327.(in Chinese)
[10]Rosihan,Arif I,Sebum C,et al.Particle Filtering Approach to Fault Detection and Isolation for GPS Integrity Monitoring[C]//Proceedings of 2006 ION GNSS.Fort Worth,TX:ION,2006:873-881.
[11]Kaplan E,Hegarty C.Understanding GPS:Principles and Applications[M].2nd ed.New York,USA:Artech House,Inc,2006:239-264.
[12]Vas wani N.Bound on errors in particle filtering with incorrect model assumptions and its implication for change detection[C]//Proceedings of 2004 IEEE International Conference on Acoustics,Speech and signal processing.Canada:IEEE,2004:729-732.
[13]Sayim I,Pervan B,Pullen S,et al.Experimental and theoretical results on the LAAS sigma over bound[C]//Proceedings of 2002 ION GPS.Manassas,Portland:ION,2002:29-39.
