基于瞬时测频的BPSK和QPSK信号参数估计*

王星，曹晋龙，＊＊，赵玉，王士岩，2，李承志

(1.空军工程大学 航空航天工程学院，陕西 西安 710038;2.解放军93286部队32分队，沈阳 110141;3.解放军93363部队，沈阳 110141)

1 引言

相位编码是雷达脉内调制技术中一种典型的调制技术，其中主要的调制形式是二相编码(BPSK)和四相编码(QPSK)。要正确地获得相位编码信号的编码规律，必须首先知道信号的载频、码速率、初始相位、码同步等各项参数，其中载频估计是对其他参数进行估计的基础。在电子侦察领域，对接收的相位编码信号的参数没有任何先验知识，对这类信号的截获、识别和参数估计存在一定的困难。针对这一问题，文献［1］提出了一种基于相位展开和最小二乘多项式拟合的算法，此算法在较低信噪比下载频估计的均方根误差依然接近相位编码信号载频估计的克拉美－罗限(Cramer－Rao)，但是该算法的复杂度较高，不宜实时处理。文献［2］给出了一种简单快速实用的非线性相位编码信号载频盲估计算法，但在电子侦察领域，对接收到的信号无法进行匹配接收，同时接收机带宽又远大于信号带宽，导致整体估计性能下降，甚至使带外噪声完全淹没信号，最终无法对载频进行估计。文献［3］对MAT算法进行了改进，提出了M－MAT算法，可以在较低信噪比条件下对QPSK信号的载频精确估计，但该算法仍然较为复杂，不易在RWR/ESM系统上实现。

瞬时测频(IFM)接收机测频分辨力高，瞬时带宽宽，实时性强，被广泛应用于RWR/ESM测频系统中。但由于传统IFM实现机理以及RWR/ESM测频资源及结构的限制，使得当前RWR/ESM系统无法通过IFM对相位编码信号的检测进行威胁告警，只是将此类信号归类为未知雷达信号。IFM若能实时检测相位编码信号，将使RWR/ESM系统具备对相位编码信号进行实时告警的能力，因此对此进行研究意义重大。为此本文根据IFM基本原理，应用仿真的方法分析BPSK和QPSK信号经过IFM系统的输出，以此为基础对传统的IFM系统进行了改进，并提出估计BPSK和QPSK信号参数的方法。

2 RWR/ESM测频系统概述

当前RWR/ESM测频系统多采用引导式测频体制，以满足空域频域宽开、实时性强和频率分辨力高的要求，测频过程可分为粗分频段、粗测频、精测频。

IFM接收机对雷达信号的测频能力直接决定RWR/ESM测频系统的测频能力。而由于IFM接收机在对雷达信号测频时，一个脉宽内只进行一次采样，因此对脉内具有相位编码特征的雷达信号是无法测频的。而当前能够检测相位编码信号的相关算法和数字接收机技术不适用于RWR/ESM系统，主要受以下两个因素的限制:

(1)当前相位编码信号检测算法虽然灵敏度较高，且具有良好的复杂信号适应能力，但是算法数学运算复杂，运算量大，导致其信号测量时间较长，实时性差，不能满足 RWR/ESM系统实时告警的需求;

(2)尽管当前较为先进的数字接收机的ADC已可达数 Gsample/s采样率，瞬时带宽已经大于1 GHz(极限值为5 GHz)，但相对于 RWR/ESM系统的瞬时覆盖带宽需求(通常数十GHz)而言，它仍是一个窄带接收机，不能满足RWR/ESM系统宽瞬时带宽的要求。目前的解决方法是采用多个窄带数字接收机拼接来满足大的瞬时带宽，拼接方式主要有时间交替多通道并行采样与信道化［4］，但按此方法体积、重量、功耗、成本代价都相当高［5］。

综上所述，目前多数RWR/ESM系统并不具备对相位编码信号的实时测频能力。那么，IFM能否在没有先验知识的情况下，实时估计相位编码信号参数呢?本文通过对IFM技术的仿真分析，发现其具备这一潜力。

3 相位编码信号的IFM仿真分析

3.1 IFM接收机原理简介

典型IFM单元为微波鉴相器(Microwave Phase Discriminator，MPD)，如图1 所示，它由功分器、延迟线、90°电桥、平方率检波器和差分放大器组成［6］。

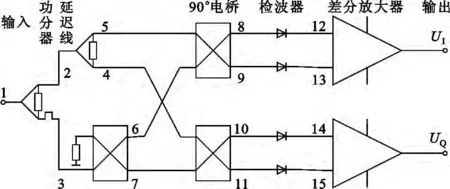
图1 实用微波鉴相器结构示意图Fig.1 Block diagram of practical MPD

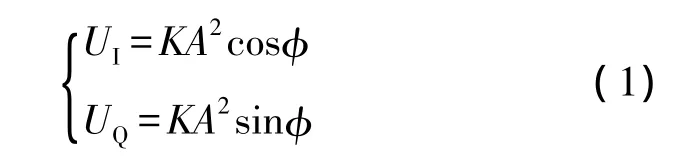
其中，相角如公式(2)所示:

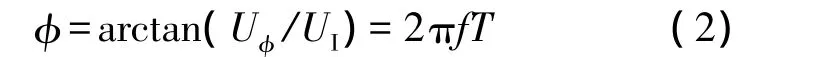
由式(1)、(2)得信号频率如公式(3)所示:

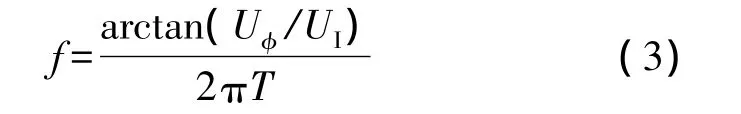
式(1)～(3)中，K为检波器系数，A为信号幅度，T为延迟线的时间延迟，f为输入信号的载频。为了解决频段覆盖和分辨率的矛盾，工程上采用图2所示IFM并联结构［7］，其多个延迟线长度符合一定关系，短延迟线支路保证测频范围，长延迟线保证精度;并根据长短延迟线之间的关系解IFM频率测量值的模糊。

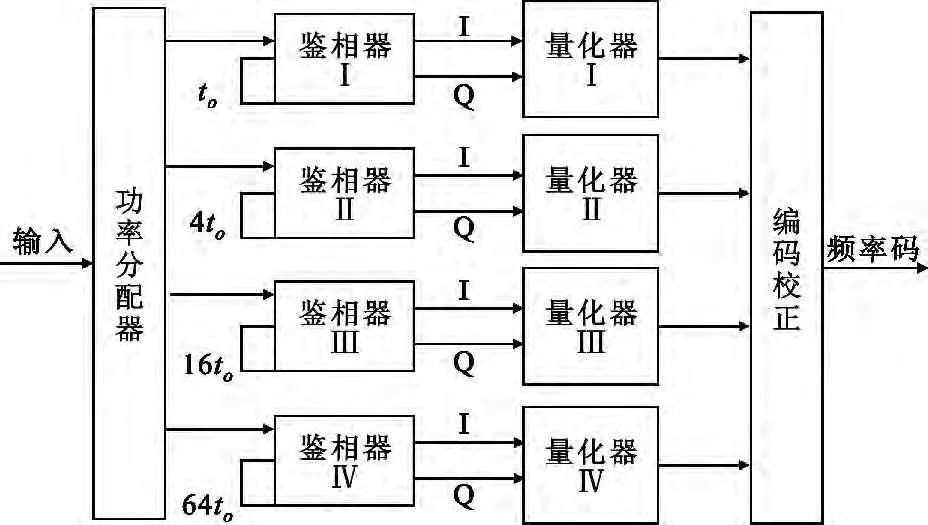
图2 传统IFM系统Fig.2 Traditional IFM system

若设图1端口1进入一个BPSK或QPSK信号，则UI、UQ的数学表达式较为复杂，下面应用MALAB仿真的方式对其进行分析。

3.2 BPSK信号的IFM仿真

BPSK信号一般模型［8］表示为

式中，q(t)为双极性伪随机序列，A为信号幅度，Tc为chip时宽，f0为载频，φn为第n个码元对应的相位，等概率时取0和π。

以13位巴克码序列［1111100110101］构造一个BPSK 信号 s(t)，A=1 V，Tc=5 μs，τ=65 μs。为便于分析，载频(设为 MHz级别)f0=2 MHz。应用MATALB进行仿真，建立三路延迟时间分别为 0.1 μs、0.4 μs、1.6 μs的并行 MPD(Maintenance Planning Document)模型。BPSK信号s(t)一个脉宽内结果如图3所示。其进入MPD模型中，输出的UI、UQ值如图4所示。

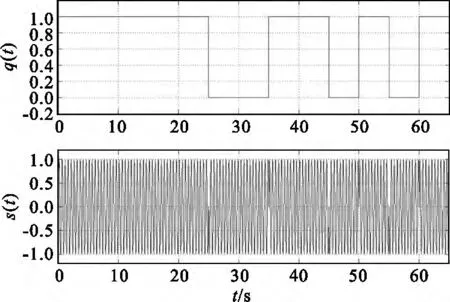
图3 BPSK信号Fig.3 BPSK signal

图4 输入为BPSK信号时MPD的UI、UQFig.4 UI、UQof MPD with BPSK signal

3.3 QPSK信号的IFM仿真

QPSK信号可以视为两路正交的BPSK信号的叠加，其一般模型［8］可表示为

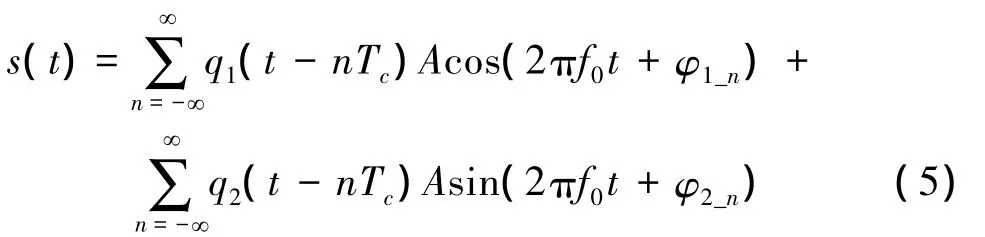
其中，q1(t)、q2(t)为两路的双极性伪随机序列，φ1_n、φ2_n为q1(t)、q2(t)的第n个码元所对应的相位。

设q1(t)、q2(t)两个序列分别为［1100001100］、［1111001111］，A=1 V，Tc=5 μs，f0=2 MHz，脉冲宽度τ=50μs。一个脉宽内的仿真结果如图5所示。此QPSK信号s(t)同样进入上述三路并行MPD模型中，输出的UI、UQ值如图6所示。

图5 QPSK信号Fig.5 QPSK signal

3.4 仿真结果分析

由以上仿真可知，BPSK和QPSK信号经过MPD后的UI、UQ为恒定电压值，而在s(t)的相位变化处存在跳变，跳变的持续时间为MPD的延迟时间。BPSK信号的UI、UQ跳变幅度恒定，而QPSK信号的UI、UQ跳变幅度变化。由此可见，这些相位跳变是存在一定规律的，若掌握了其中的规律，即可对BPSK和QPSK信号的相关参数进行估计。但传统的IFM系统对一个脉宽的信号只进行一次采样，无法得到跳变信息，因此需对传统的IFM系统进行改进。

图6 输入为QPSK信号时MPD的UI、UQFig.6 UI、UQof MPD with QPSK signal

4 IFM系统改进

4.1 改进的IFM系统概述

由以上分析可知，可用ADC代替传统IFM系统中的极性量化器，对MPD输出的UI、UQ进行连续时间采样，检测到相位变化处的跳变信息。根据跳变信息对BPSK和QPSK信号进行区分识别，采用相关算法对离散的UI、UQ进行数字解算，进而估计出BPSK和QPSK信号的相关参数。

改进后的IFM如图7所示，具有如下两个典型特征:

(1)采用高精度ADC代替量化器结构，通过数字解算不仅可解模糊，且可以获得更多信号特征;

(2)信号检波的包络经过整形后，作为信号有效信号。在其有效持续时间内，用ADC对UI、UQ进行连续时间采样，对采样结果进行结算。

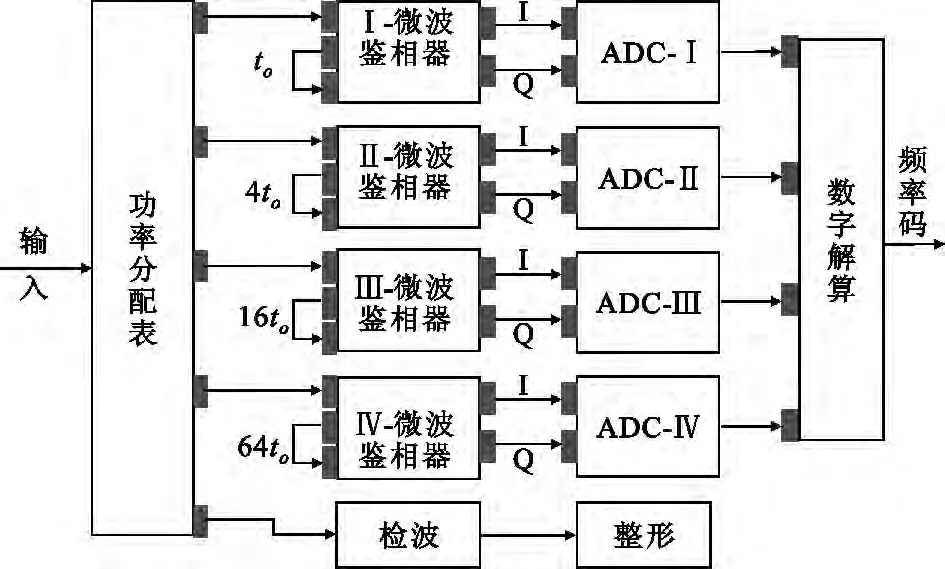
图7 改进后的IFM系统Fig.7 The modified IFM system

4.2 测频分辨力分析

由于改进IFM系统是对UI、UQ单独采样量化，而不是采用传统IFM系统中的极性量化，因此可对式(3)求全微分，得改进后一路鉴相器的频率分辨力如公式(6)所示:

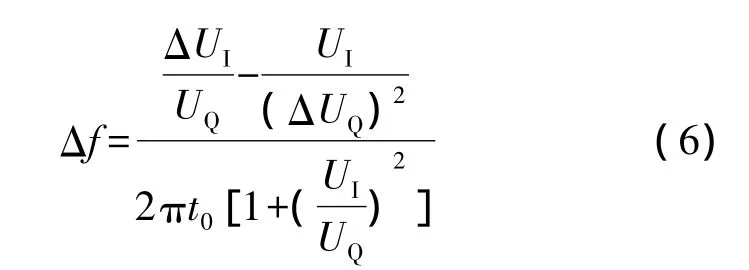
式中，ΔUI、ΔUQ是 ADC 对 UI、UQ的量化间隔。图7所示四路鉴相器并行运用的改进后IFM系统，其频率分辨力如公式(7)所示:

5 BPSK、QPSK信号参数估计

5.1 BPSK、QPSK 信号检测识别

估计BPSK和QPSK信号参数的前提是必须区分这两种信号。根据文献［9］可知，利用不同信号的相位差分变化规律可以有效地识别BPSK和QPSK信号。本文MPD输出的相位是指由延迟线引起的相位差，这与文献［9］中的差分相位本质是一样的，不同的是文献［9］中的差分相位是应用微分的方法求得，是理论方法，而本文中相位差是应用IFM鉴相的方法求得，是一种硬件实现方法，更具有实际意义。下面具体分析BPSK和QPSK的识别方法。

BPSK和QPSK信号经过MPD后的输出相位结果在幅度上明显不同，前者的输出结果幅度只跳变一次，后者输出结果幅度跳变三次。这是因为BPSK信号码元对应相位φn为两个值，一般为0和π，s(t)的相位跳变一次，跳变值为π;而QPSK信号的码元对应相位φn为4个值，假设φn=［0π/2 π 3π/2］，s(t)的相位跳变三次，跳变值为π/2、π和3π/4。根据上述规律，可设定门限值对BPSK和QPSK信号进行区分。若MPD的输出结果等幅跳变，则可判定输入为BPSK信号;若MPD输出结果幅度跳变三次，则可判定输入为QPSK信号。区分BPSK和QPSK信号后，可对信号的载频、码元及码周期进行估计。

5.2 载频估计

为模拟实际情况，在仿真中对BPSK和QPSK信号加入信噪比为10dB噪声。用采样频率为10MHz的 ADC 对 MPD1、MPD2、MPD3输出的UI、UQ值进行采样量化，由公式(3)可得离散频率值，应用解模糊算法［10］，消除长延迟线支路的模糊，并剔除相位跳变点得结果如图8所示。对第三路输出的精度较高的离散频率值取平均，BPSK信号载频估计=1.9979 MHz，QPSK信号载频估计=2.0012 MHz。

图8 频率输出Fig.8 QPSK signal

改变信噪比，仿真500次的均方根误差结果如图9所示。由图可知，随信噪比的增加，误差逐渐减小。BPSK信号的误差曲线比QPSK信号的误差曲线要平滑，这是因为BPSK信号在测频时所产生的跳变点恒定，而QPSK信号的跳变点不恒定。当信噪比大于5 dB时，测频的均方根误差收敛于 0.05 MHz。

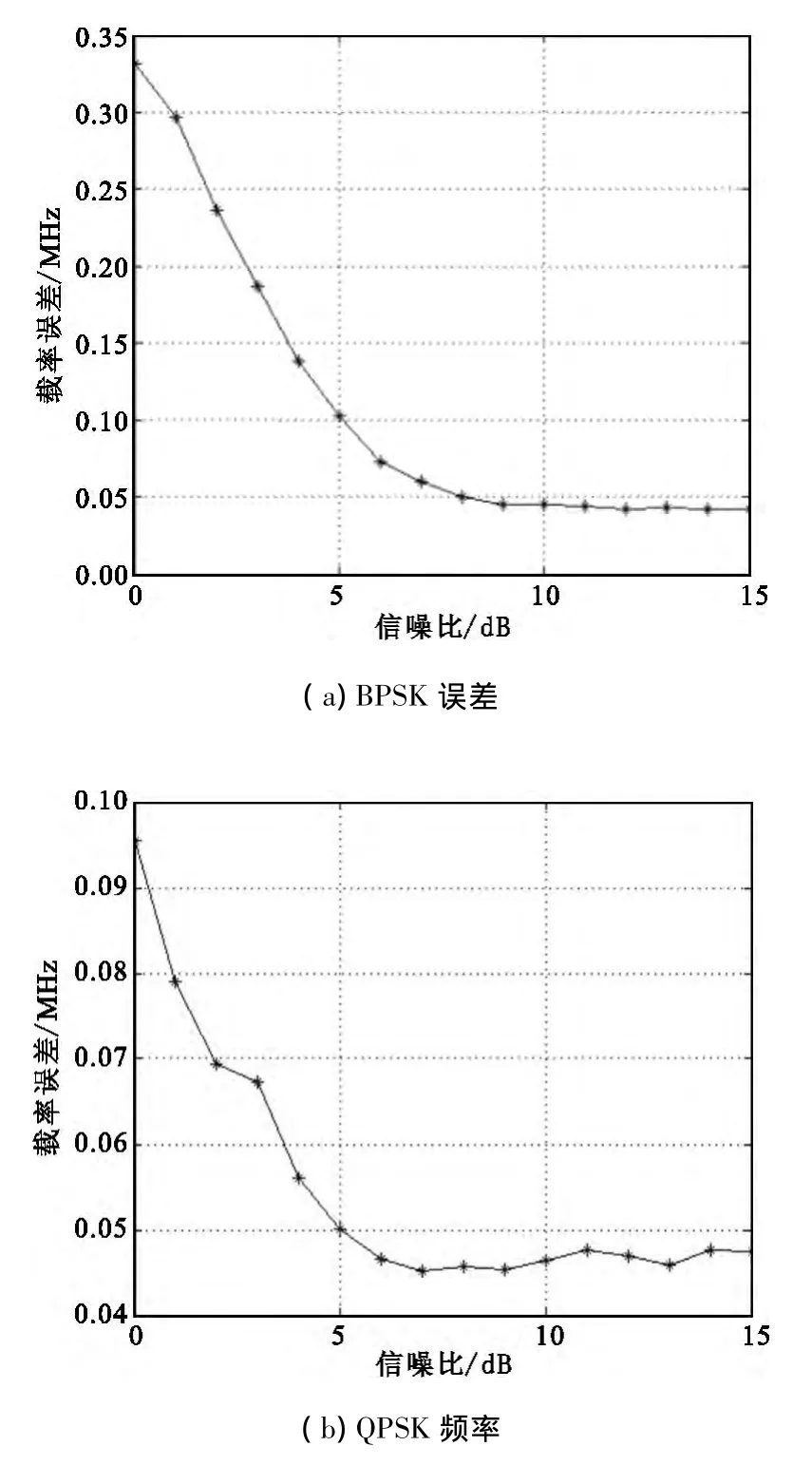
图9 测频误差与信噪比关系Fig.9 Relationship between SNR and error frequency measurement

本文只对三路MPD进行了仿真，这是由于相位跳变的持续时间与延迟线产生的延时时间相等，按各路MPD延时间的倍数关系，第四路MPD的延时为6.4 μs，此时相位跳变的持续时间大于码元宽度，UI、UQ会发生严重失真，使载频无法估计。而实际雷达信号的载频为几GHz至几十GHz之间，因此MPD的延迟时间为ns数量级别。典型的四路MPD的延迟时间为 0.15 ns、0.6 ns、2.4 ns、9.6 ns，一般远小于码元宽度，因此不会造成UI、UQ的失真。此时第四路会输出更高精度的测量结果，一般比第三路高一个数量级。因此，信噪比大于5 dB时可到达当前IFM的精度要求。

5.3 码元和码周期估计

BPSK信号的码元只有0和1，因此可根据UI、UQ的幅度跳变信息直接估计得到，即相位跳变判别法。每当相位幅度跳变一次，码元相应变化一次，跳变的最小时间间隔即为码周期。

QPSK信号的码元估计可采两种方法。

一种是如上述的相位跳变判别法。QPSK信号的UI、UQ的幅度跳变信息有正值和负值，不易找出其变化规律。因此对UI、UQ取反正切，得相位值如图10所示，此处相位值是由延时线引起的相位差。由于在解模糊的过程中，相位跳变点会被剔除，因此图10是未解模糊的结果。

图10 QPSK的相位差Fig.10 Phase difference of QPSK

下面就其相位跳变规律进行分析。QPSK信号的码元有4个:00，01，11和10。假设其相位分别为φn=［0，π/2，π，3π/2］，那么码元之间的变化规律与相位跳变之间的变化规律的关系如图11所示，码元从00到01，相位跳变π/2;码元从00到11，相位跳变π;码元从00到10，相位跳变3π/2。因此可得出如下规律:相邻码元之间的相位跳变值最小，间隔两个码元之间的相位跳变值最大，间隔一个码元之间的相位跳变值在上述两个之间。按此规律分析图10中MPD3输出相位，假设初始码元为11，在10μs处相位跳变最小，码元由11变为10;在15 μs处相位跳变最大，码元由10变为11;在20μs处相位跳变在最大值与最小值之间，码元由11变为00。同理，在30μs和40μs处相位也有跳变，码元依次为11和10。根据相位跳变的最小时间间隔可得码周期为5 μs，由此可估计出码元为［11111011000011111010］。其中码元高位对应q2(t)的估计值，为［1111001111］;低位对应 q1(t)估计值，为［1100001100］。

图11 相位跳变与码元关系图Fig.11 Relationship between symbol and phase jump

另一种方法是应用相干解调法，此方法的前提是必须已知信号载频，而在RWR/ESM系统中，信号载频属未知参数，因此可用载频估计值^fQPSK代替原始信号载频，实际应用中可用窄带接收机输出的精测频数据对本振进行引导。码元估计原理如图12所示。

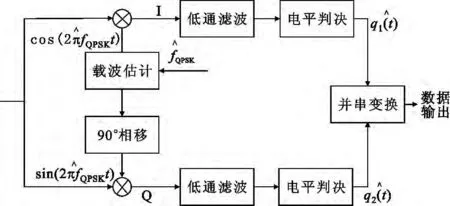
图12 相干解调法原理图Fig.12 Schematic diagram of coherent demodulation

根据原理框图进行建模仿真，结果如图13所示，图中码元估计的延迟是由于滤波延迟所造成的。

图13 相干解调法估计的QPSK信号码元Fig.13 QPSK signal symbol of coherent demodulation

综合上述分析，两种方法各有其优缺点:相位跳变判别法较为简便，实时性好，适用于RWR/ESM系统，但码元初始值未知则无法完成估计，因此需要一定的先验知识才能估计出码元;相干解调法不需要任何先验知识，但对信号载频的估计精度要求较高，且实时性不如相位跳变判别法，因此这种方法适用于电子情报侦察，得到码元估计值可作为建立码元数据库的基础。

6 结束语

本文应用仿真的方法分析了IFM系统对相位编码信号(二相编码和四相编码信号)处理情况，提出了基于IFM的相位编码信号的载频和码元估计算法，其原理简单，计算量小，实时性好，适用于RWR/ESM系统中。本文的研究为今后RWR/ESM系统测频接收机的研制和改进提供了一种新的思路，有较好的实际应用价值。

［1］邓振淼，刘渝.MPSK信号载频盲估计［J］.通信学报，2007，28(2):94－100.DENG Zhen－miao，LIU Yu.Blind estimation of MPSK carrier frequency［J］.Journal on Communications，2007，28(2):94－100.(in Chinese)

［2］Ghogho M，Swami A，Durrani T.Blind estimation of frequency offset in the presence of unknown multipath［C］//Proceedings of 2000IEEE International Conference on Personal Wireless Communications. Piscataway， NJ:IEEE，2000:104－108.

［3］朱霞，刘渝，狄慧.一种低信噪比条件下QPSK信号盲处理方法［J］.数据采集与处理，2011，26(5):555－558.ZHU Xia，LIU Yu，DI Hui.Blind Processing Met－hod for QPSK Signal under Low SNR［J］.Journal of Data Acquisition ＆ Processing，2011，26(5):555－558.(in Chinese)

［4］王洪.宽带数字接收机关键技术研究及系统实现［D］.成都:电子科技大学，2007.WANG Hong.Research and Implementation of system on Wide band Digital Receiver and Key Technologies［D］.Chengdu:University of Electronic Science and Technology of China，2007.(in Chinese)

［5］王坤达.基于实时数字信号处理的宽带单比特瞬时测频接收技术［J］.舰船电子对抗，2012，35(3):31－36.WANG Kun－da.Wide band single－bit IFM receiving technology based on real－time digital signal processing［J］.Shipboard Electronic Countermeasure，2012，35(3):31－36.(in Chinese)

［6］王星.航空电子对抗原理［M］.北京:国防工业出版社，2008.WANG Xing.Principles of aircraft electronic countermeasure［M］.Beijing:National Defense Industry Press，2008.(in Chinese)

［7］张学成.宽带大动态瞬时测频接收机的设计与实现［J］.舰船电子对抗，2011，34(4):29－31.ZHANG Xue－cheng.Design and realization of wide band instantaneous frequency measurement receiver with large dynamic range［J］.Shipboard Electronic Countermeasure，2011，34(4):29－31.(in Chinese)

［8］Skolnik M L.雷达手册［M］.南京电子技术研究所，译.北京:电子工业出版社，2010.Skolnik M L.Radar Handbook［M］.Translated by Nanjing Institute of Electronic Technology.Beijing:Publishing House of Electronics Industry，2010.(in Chinese)

［9］黄知涛，周一宇.一种有效的BPSK/QPSK信号调制识别方法［J］.电子对抗技术，2005，20(2):10－13.HUANG Zhi－tao，ZHOU Yi－yu.An effective approach to the recognition of BPSK/QPSK signals［J］.Electronic Warfare Technology，2005，20(2):10－13.(in Chinese)

［10］唐永年.雷达对抗工程［M］.北京:北京航空航天大学出版社，2012:195－198.TANG Yong－nian.Engineering of radar counter measure［M］.Beijing:Publishing House of Beijing University of Aeronautics and Astronautics，2012:195－198.(in Chinese)