应用开源程序进行矿业地质统计学中的三维变差函数分析

方晓刚，李宇鹏

（中国石油大学（北京），北京102249）

地质统计学发源于矿业领域，并日益扩展至石油、环境、水文、农林等领域［1－5］。理论上可以对于任何空间上即具有随机性又具有结构性的自然现象进行研究。而变差函数是经典地质统计学中一个重要工具，它能够反映地质变量的空间变化特征—相关性和随机性。因为其能透过随机性反应空间变量的结构性，因此也称为结构函数，进行变差函数分析，有时也称为空间变量的结构分析［2］。

目前很多空间数据分析及绘图商业软件如Surfer，MapGIS，……等以及矿业储量评估软件等等均具有地质统计学模块。可以使用它们进行变差函数分析以及变量空间插值等。虽然这些这些商业软件提供了不同的分析界面，成果的可视化也不尽相同，但是如此众多的商业软件所使用的方法都是建立现有的成熟的算法之上。而往往这些算法原理都是一致的，且都是公开发表的，并且都有随之而来的开源程序。使用这些开源的程序不仅可以节约花费在使用商业软件的培训和维护费用，而且基于开源程序的优点是分析的结果过程透明，参数可控，原理明了，所以可以根据具体数据进行特殊的研究，满足具体矿山开发的需要。

文章对地质统计分析中最基本的过程：变差函数的分析过程进行了详尽说明。这一个过程包括对数据的检查、数据正态转换、实验变差函数的求取，以及理论变差函数的人工及自动拟合等。文中对每一步骤的重要性，以及所使用的开源程序作为论述的重点，而对每一步的理论基础没有做过多的阐述，指出一定的参考文献，感兴趣的读者可以进一步的学习。

1 程序与数据体介绍

在众多的公开发布的程序中，应用最广泛的当属美国Stanford大学的开发的Gslib地质统计学程序库（可以在http：//www.gslib.com免费下载）［6］。程序可以在任何操作系统下顺利运行。并且有源程序代码（Fortran 90）下载，便于感兴趣进行更深入的学习和应用。其它的开源软件则有GeoR，Gstat等［7－8］。

使用Gslib时，所有程序运行所读入的数据文件应符合Geo－eas的格式［6］。即文本的第一行为注释行，给出简单的数据说明。第二行为数据列数nvar（number of variables），即共有多少列数据。由第三行开始则为这nvar列数据的名称，每一行为一列数据的名称。之后为nvar列数据。图1中给出了一个数据文件的前9行。

图1 数据文件例子

所有Gslib程序的运行都采用了参数文件的方式。即程序运行后要求输入参数文本，运算所需要的设置都通过参数文件提供给程序。程序初次运行时会生成一个默认的参数文件，使用者可以根据自己的实际情况修改样本参数文件，重新运行程序即可。程序运行时所生成的图形文件都保存为postscript文档格式。推荐使用GSview程序打开（Http：//pages.cs.wisc.edu/～ghost/gsview/免费下载）。

地质统计学起源于矿业，最基本的应用仍然是矿产资源的品位估计和储量计算。文章所使用的数据是由Pierre Mousset Jones提供给地质统计学研究领域的一套真实的Brenda矿场3D数据体［9］。Brenda矿场是一个铜/钼矿体，位于British Columbia（位于Central Okanagan的Peachland以西大概22km处）。数据包括各点x、y、z坐标，铜钼的百分含量，以及取样的长度和顶底深度。文中仅选用了铜含量的数据进行说明。

2 变差函数分析

2.1 数据收集与检查（Exploratory data analysis）

进行变差函数分析的第一步就是对原始数据的探索性分析（EDA：Exploratory data analysis）。可以说EDA本身并不能算一个方法或者技术，它主要是一种我们在进行地质统计学分析时所应持有的态度，即基于数据的客观态度。在对于矿业原始数据的EDA主要包括对原始数据空间位置分布，均值和方差统计，以及分布形态检查等。通过这些简单的统计可以对所取得的数据获得一个大的了解，便于开展后期工作。

经过简单的直方图绘制，可以得出数据的均值，标准差以及其他的一下分布形态参数。绘制直方图可以使用GSLIB程序中Histplt程序。图2是此数据集中铜钼原始数据的直方图。不仅可以看出其分布比较接近与对数分布，而且还可以识别出一些异常值。例如在此数据集中，铜的百分含量就出现了1.024这样的一个数据点。就有必要对此点数据进行检查。实际工作中如果有条件的话，应该重新测量。在这里，可以简单的将其设置为全区的均值0.664。重新绘制直方图如图2所示。

2.2 数据正态转换（Normal score data transformation）

经过初步的检查认为数据中人为的错误基本上消除之后就可以开始下一步的工作。由于后期的克里格估计（kriging estimation）以及随机模拟都假设数据服从正态分布［1－2］，所以必须对数据进行正态转换，而且正态转换后有利于变差函数拟合步骤中基台值的设定。

对原始数据的正态转换，可以使用Gslib中的Nscore程序，。在此转换中是使用了基于原始数据概率分布的分位数转换，最大限度的保证了原始数据的分布形态［6］。使用分位数进行正态转换一般要求样本点的个数比较多。当点对个数较少时（少于50个）可以使用Histsmth程序对原始数据进行光滑，之后再进行正态转换比较可靠［6］。在一般的矿业变差函数分析中，原始数据的个数应该是可以满足使用分位数的Nscore转换。将数据由正态恢复至原始分布的转换则是使用Backtr程序进行。如果是使用Gslib中的Sgsim做随机模拟的话，程序提供了一个是否自动转换的控制参数。如果想在Sgsim模拟结果直接显示为原始数据，则需要提供nscore程序运行时产生的转换分位数表。如本例中转换完后的数据直方图如图3所示。

图2 铜含量直方图分布

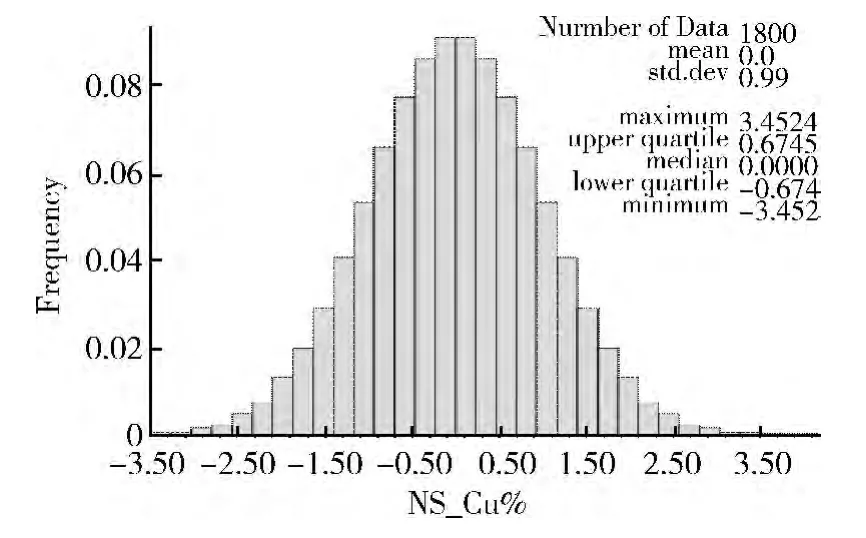
图3 铜含量正态数据直方图

2.3 试验变差函数分析（Experimental Variogram Calculation）

几乎所有的空间变量都是具有各向异性的特征。而这种空间的变异性则是由变差函数来表征。这种空间变异通过所拟合的理论模型，最终将体现在对空间变量的估值或者是模拟中。所以变差函数的求取是非常重要的一步。经典地质统计学中认为，在本征假设条件下，理论变差函数γ（α，｜h｜）是沿空间任一方向α，相距为｜h｜的两个区域化变量z（x）和z（x＋h）的增量的方差，见式（1）。

式中：h称为滞后距（lag），是一个矢量距离，决定于方向α和之间的距离增量｜h｜。在实际的计算中，把由取样点计算而来的变差函数称为实验变差函数（experimental variogram），记为（h），它是理论变差函数γ（h）的估计值。计算公式见式（2）。

式中：N（h）是具有相同滞后距的点对个数。所以试验变差函数是求取了［z（x）－z（x＋h）］的算术平均值。对于不同的滞后距分别计算相应的（h），这些点绘在h－（h）图上则为试验变差函数图。

使用Gslib计算并绘制试验变差函数图主要用到两个程序Gamv和Vargplt两个程序。利用Gamv是依据式（2）来计算变差函数，使用vargplt这个程序绘图。

在Gamv程序的运行中几个关键的参数包括：变差函数计算方向、方向容限、滞后距，滞后距容限等几个参数，见图4。由于试验变差函数取决于方向α，所以必须首先选定方向。而由于在选定的方向上可能的点对比较少，所以根据地质实际情况可以设定一个容限。对于滞后距的选择一般选择多数样品的间距作为滞后距，同样由于一个滞后距不可能提供足够多的点对计算一个较稳定的算术平均值，所以对于一个滞后距也可以设定一个容限。同时也要考虑滞后距的个数（nlag），一般来说nlag＊lag应该覆盖是搜索方向样本点分布区域的1.5倍。

图4 试验变差函数参数设定

利用本数据集，沿x，y方向计算的试验变差函数如图5所示。在用Vargplt进行绘图后，可以根据计算结果调整Gamv程序中计算试验变差函数所需要的滞后距、滞后距个数以及角度容限等参数，然后重新计算重新绘图。经过这样几个反复的调整，使得能沿着选定的方向稳定试验变差函数应该能达到数据的总基台值（Sill）值。但是注意在带状各向异性（zonal anisotropy）的影响可能无法达到基台值。本例中，由于之前进行了正态转换，所以数据的基台值应该就是1.0。沿此方向的变程（r）则是试验变差函数达到基台值时的滞后距。

图5 X、Y方向试验变差函数图

在绘出试验变差函数后，应该首先检查的是否与我们对于此区域的地质认识符合。而另一方面试验变差函数又可以佐证我们的地质分析，二者应该是相辅相成的。如此例中，可以得出铜含量数据在X方向和Y方向上没有很大的差异，基本上是具有相同的空间变异性。

2.4 理论变差函数拟合

试验变差函数仅在所选定的方向上，在不同的滞后距位置进行了计算，而实际空间估值时是需要一个理论上满足正定性要求，并且在空间任何方向上，任何距离都可以求取值的函数［6］。这就需要用理论的变差函数模型来拟合试验变差函数。经典的理论变差函数模型主要有，球状模型，指数模型，高斯模型以及纯块金效应模型等［6］。而对于试验变差函数的拟合需要使用Gslib中的Vmodel和Vargplt程序。

具体的拟合过程是：首先通过观察试验变差函数确定基台值，变程以及理论变差函数类型，比如此例中，可以设定沿X，Y方向的块金效应值设为0.3；理论模型可以选指数模型（exponential model），基台值取0.7。将以上参数输入Vmodel程序的参数文件，可以计算理论变差函数值。然后用Vargplt将二者绘制在同一图中进行观察。如果认为需要调整，则可以重新调整Vmodel中的变程，和基台值等，然后重新计算，绘制进行观察。这样进行调整直至合适。本例中拟合的结果如图6所示。本例中，拟合的结果用数学公式表示。

图6 理论变差函数的人工拟合结果

在人工拟合，目视检查的过程中可以体现我们的主动性，而且在拟合过程中的不断的调整理论模型的参数等可以加深我们对于研究区的认识，增加我们分析变差函数的经验。

2.5 理论变差函数自动拟合（varfit）

人工拟合虽然可以将我们的认识体现在最终的拟合结果中，但同时这也是一种主观性，过则不及。为了避免过度的主观性，而且为了快速的对众多的变差函数进行拟合，不少学者发表了自动拟合的程序，此处选用了Eulogio Pardo－Iguzquiza在1999年发表的Varfit程序［10］。程序中使用了加权最小二乘法拟合各个试验变差函数点。本例中使用自动拟合的结果如图7所示。

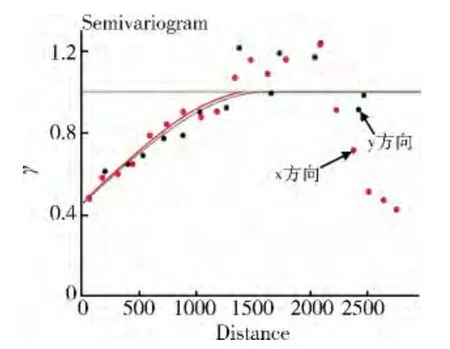
图7 使用程序varfit人工拟合结果

自动拟合的结合，用数学公式表达。

用自动拟合软件可以减轻我们的工作量，但建模者的认识和思想是任何软件都无法取代的。做好这项工作要求把数学与地质相结合。研究者既要比较了解熟悉研究区的的地质背景，同时对地质统计学有一定的了解。

3 结论

利用开源程序完全可以进行地质统计中的各项工作，将这套过程和方法总结起来可以很好地指导矿产的勘探。正确运用这一过程和方法可以最大限度的减少变差函数分析过程中的人为因素造成的失误和错误，同时开源程序分析环境的搭建使得从事变差函数的过程更透明，更可控。更好的指导矿产的勘探工作。文章仅以地质统计学分析中最基本的步骤变差函数分析为例进行了说明。实际工作中的后续工作则是尽可能的利用原始数据对拟合的理论变差函数进行交叉验证。如果满足误差要求则可以将拟合的变差函数应用到空间插值或者是随机模拟。

［1］ Matheron G.Principle of geostatistics［J］.Economic Geology，1963，58（8）：1246－1266.

［2］ Wackernagel H.Multivariate Geostatistcs［M］.Berlin Heidelberg：Springer－Verlag，2003.

［3］ Atkinson P.M.，Lioyd C.D.Geostatistics for Environmental Applications［M］.London：Springer，2010.

［4］ Webster R.，Oliver M.A.Geostatistics for environmental scientists［M］.John Wiley＆Sons，2007.

［5］ Oliver M.A.Geostatistical Applications for Precision Agriculture［M］.LondonSpringer，2010.

［6］ Deutsch C.V.，Journel A.G，GSLIB：Geostatistical Software Library and User′s Guide［D］.Oxford University Press，1997.

［7］ http：//www.leg.ufpr.br/geoR/.

［8］ http：//www.gstat.org/.

［9］ Clark I.Practical Geostatistics［M］.London，Applied Science Publishers，1979.

［10］ Pardo－Igúzquiza，Eulogio VARFIT：a fortran－77program for fitting variogram models by weighted least squares［J］.Computers ＆Geosciences，1999，25（3）：251－261.